算法系列15天速成 第五天 五大经典查找【中】

哈希查找：

对的，他就是哈希查找，说到哈希，大家肯定要提到哈希函数，呵呵，这东西已经在我们脑子里面形成
固有思维了。大家一定要知道“哈希“中的对应关系。
     比如说： ”5“是一个要保存的数，然后我丢给哈希函数，哈希函数给我返回一个”2"，那么此时的”5“
和“2”就建立一种对应关系，这种关系就是所谓的“哈希关系”，在实际应用中也就形成了”2“是key，”5“是value。
    那么有的朋友就会问如何做哈希，首先做哈希必须要遵守两点原则：
          ①:  key尽可能的分散，也就是我丢一个“6”和“5”给你，你都返回一个“2”，那么这样的哈希函数不尽完美。
          ②： 哈希函数尽可能的简单，也就是说丢一个“6”给你，你哈希函数要搞1小时才能给我，这样也是不好的。

其实常用的做哈希的手法有“五种”：
第一种：”直接定址法“。
                  很容易理解，key=Value+C； 这个“C"是常量。Value+C其实就是一个简单的哈希函数。
第二种：“除法取余法”。
                  很容易理解， key=value%C;解释同上。
第三种：“数字分析法”。
                  这种蛮有意思，比如有一组value1=112233，value2=112633，value3=119033，
                  针对这样的数我们分析数中间两个数比较波动，其他数不变。那么我们取key的值就可以是
                  key1=22,key2=26,key3=90。
第四种：“平方取中法”。此处忽略，见名识意。
第五种：“折叠法”。
                 这种蛮有意思,比如value=135790，要求key是2位数的散列值。那么我们将value变为13+57+90=160，
                 然后去掉高位“1”,此时key=60，哈哈，这就是他们的哈希关系，这样做的目的就是key与每一位value都相
                 关，来做到“散列地址”尽可能分散的目地。

正所谓常在河边走，哪有不湿鞋。哈希也一样，你哈希函数设计的再好，搞不好哪一次就撞楼了，那么抛给我们的问题
就是如果来解决“散列地址“的冲突。

其实解决冲突常用的手法也就2种：

第一种： “开放地址法“。
                 所谓”开放地址“，其实就是数组中未使用的地址。也就是说，在发生冲突的地方，后到的那个元素（可采用两种方式
                 :①线性探测，②函数探测）向数组后寻找"开放地址“然后把自己插进入。

第二种：”链接法“。
                这个大家暂时不懂也没关系，我就先介绍一下原理，就是在每个元素上放一个”指针域“，在发生冲突的地方，后到的那
               个元素将自己的数据域抛给冲突中的元素，此时冲突的地方就形成了一个链表。

上面啰嗦了那么多，也就是想让大家在”设计哈希“和”解决冲突“这两个方面提一点参考和手段。

那么下面就上代码了，
     设计函数采用：”除法取余法“。
     冲突方面采用:”开放地址线性探测法"。

代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace HashSearch
{
    class Program
    {
        //“除法取余法”
        static int hashLength = 13;

//原数据
        static List<int> list = new List<int>() { 13, 29, 27, 28, 26, 30, 38 };

//哈希表长度
        static int[] hash = new int[hashLength];

static void Main(string[] args)
        {
            //创建hash
            for (int i = 0; i < list.Count; i++)
            {
                InsertHash(hash, hashLength, list[i]);
            }

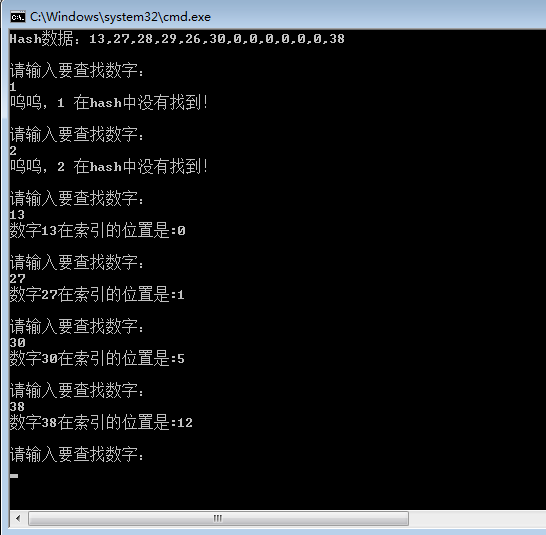
Console.WriteLine("Hash数据：" + string.Join(",", hash));

while (true)
            {
                Console.WriteLine("\n请输入要查找数字：");
                int result = int.Parse(Console.ReadLine());
                var index = SearchHash(hash, hashLength, result);

if (index != -1)
                    Console.WriteLine("数字" + result + "在索引的位置是:" + index);
                else
                    Console.WriteLine("呜呜，" + result + " 在hash中没有找到！");

}
        }

///<summary>
/// Hash表检索数据
///</summary>
///<param name="dic"></param>
///<param name="hashLength"></param>
///<param name="key"></param>
///<returns></returns>
        static int SearchHash(int[] hash, int hashLength, int key)
        {
            //哈希函数
            int hashAddress = key % hashLength;

//指定hashAdrress对应值存在但不是关键值，则用开放寻址法解决
            while (hash[hashAddress] != 0 && hash[hashAddress] != key)
            {
                hashAddress = (++hashAddress) % hashLength;
            }

//查找到了开放单元，表示查找失败
            if (hash[hashAddress] == 0)
                return -1;
            return hashAddress;

}

///<summary>
///数据插入Hash表
///</summary>
///<param name="dic">哈希表</param>
///<param name="hashLength"></param>
///<param name="data"></param>
        static void InsertHash(int[] hash, int hashLength, int data)
        {
            //哈希函数
            int hashAddress = data % 13;

//如果key存在，则说明已经被别人占用，此时必须解决冲突
            while (hash[hashAddress] != 0)
            {
                //用开放寻址法找到
                hashAddress = (++hashAddress) % hashLength;
            }

//将data存入字典中
            hash[hashAddress] = data;
        }
    }
}

结果：

索引查找：
     一提到“索引”，估计大家第一反应就是“数据库索引”，对的，其实主键建立“索引”，就是方便我们在海量数据中查找。
关于“索引”的知识，估计大家都比我清楚，我就简单介绍下。
我们自己写算法来实现索引查找时常使用的三个术语：
第一：主表，      这个很简单，要查找的对象。
第二：索引项，   一般我们会用函数将一个主表划分成几个子表，每个子表建立一个索引，这个索引叫做索引项。
第三：索引表,    索引项的集合也就是索引表。

一般“索引项”包含三种内容：index，start，length

第一： index，也就是索引指向主表的关键字。
第二：start， 也就是index在主表中的位置。
第三：length, 也就是子表的区间长度。

代码如下:

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace IndexSearchProgram
{
    class Program
    {
        ///<summary>
/// 索引项实体
///</summary>
        class IndexItem
        {
            //对应主表的值
            public int index;
            //主表记录区间段的开始位置
            public int start;
            //主表记录区间段的长度
            public int length;
        }

static void Main(string[] args)
        {
            Console.WriteLine("原数据为：" + string.Join(",", students));

int value = 205;

Console.WriteLine("\n插入数据" + value);

//将205插入集合中，过索引
            var index = insert(value);

//如果插入成功，获取205元素所在的位置
            if (index == 1)
            {
                Console.WriteLine("\n插入后数据：" + string.Join(",", students));
                Console.WriteLine("\n数据元素：205在数组中的位置为 " + indexSearch(205) + "位");
            }

Console.ReadLine();
        }

///<summary>
/// 学生主表
///</summary>
        static int[] students = {
                                   101,102,103,104,105,0,0,0,0,0,
                                   201,202,203,204,0,0,0,0,0,0,
                                   301,302,303,0,0,0,0,0,0,0
                                };
        ///<summary>
///学生索引表
///</summary>
        static IndexItem[] indexItem = {
                                  new IndexItem(){ index=1, start=0, length=5},
                                  new IndexItem(){ index=2, start=10, length=4},
                                  new IndexItem(){ index=3, start=20, length=3},
                                };

///<summary>
/// 查找数据
///</summary>
///<param name="key"></param>
///<returns></returns>
        public static int indexSearch(int key)
        {
            IndexItem item = null;

// 建立索引规则
            var index = key / 100;

//首先去索引找
            for (int i = 0; i < indexItem.Count(); i++)
            {
                if (indexItem[i].index == index)
                {
                    item = new IndexItem() { start = indexItem[i].start, length = indexItem[i].length };
                    break;
                }
            }

//如果item为null，则说明在索引中查找失败
            if (item == null)
                return -1;

for (int i = item.start; i < item.start + item.length; i++)
            {
                if (students[i] == key)
                {
                    return i;
                }
            }
            return -1;
        }

///<summary>
/// 插入数据
///</summary>
///<param name="key"></param>
///<returns></returns>
        public static int insert(int key)
        {
            IndexItem item = null;
            //建立索引规则
            var index = key / 100;
            int i = 0;
            for (i = 0; i < indexItem.Count(); i++)
            {
                //获取到了索引
                if (indexItem[i].index == index)
                {
                    item = new IndexItem()
                    {
                        start = indexItem[i].start,
                        length = indexItem[i].length
                    };
                    break;
                }
            }
            if (item == null)
                return -1;
            //更新主表
            students[item.start + item.length] = key;
            //更新索引表
            indexItem[i].length++;
            return 1;
        }
    }
}

结果：

ps： 哈希查找时间复杂度O(1)。

索引查找时间复杂度：就拿上面的Demo来说是等于O(n/3)+O(length)