使用python绘制3维正态分布图的方法

今天使用python画了几个好玩的3D展示图，现在分享给大家。

先贴上图片

使用的python工具包为：

from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

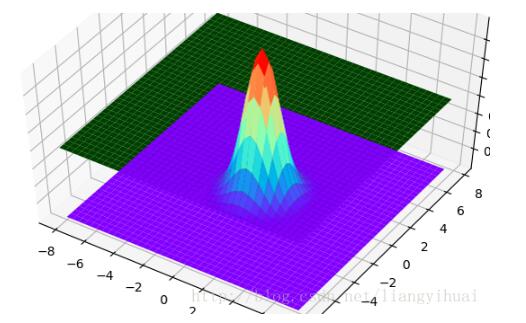
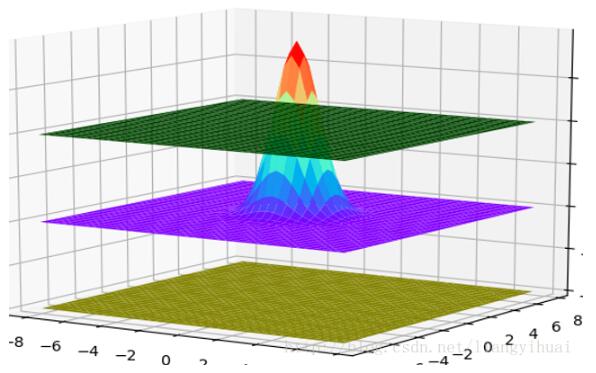
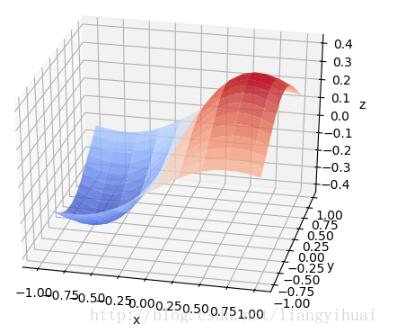
在贴代码之前，有必要从整体上了解这些图是如何画出来的。可以把上面每一个3D图片理解成一个长方体。输入数据是三维的，x轴y轴和z轴。在第三个图片里面有x、y和z坐标的标识。在第三张图片中，我们可以理解为，z是随着x和y变化的函数。就像一个人在山丘地区走动一样，其中x和y表示的是方向，z表示的这个人在上坡还是下坡。第二张图片的中间那个，其实是一个3维的正态分布图。

具体的公式为：

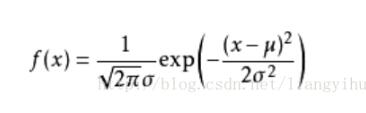
上面的是2维的，即只有x和y，如果是三维的话，需要一点变形，只需要在上面的公式基础之上把exp（）里面改变为：exp(-((x-u)^2 + (y - u)^2)/(2q^2)), 这里的u表示平均值，q表示标准差。这样变化之后，z = f(x, y)。这就是z值的公式了，表示的是z值随着x和y值的变化而变化的函数。

下面贴一下代码

这是第二张图片的代码。

from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
len = 8;
step = 0.4;

def build_layer(z_value):
 x = np.arange(-len, len, step);
 y = np.arange(-len, len, step);
 z1 = np.full(x.size, z_value/2)
 z2 = np.full(x.size, z_value/2)
 z1, z2 = np.meshgrid(z1, z2)
 z = z1 + z2;

 x, y = np.meshgrid(x, y)
 return (x, y, z);

def build_gaussian_layer(mean, standard_deviation):
 x = np.arange(-len, len, step);
 y = np.arange(-len, len, step);
 x, y = np.meshgrid(x, y);
 z = np.exp(-((y-mean)**2 + (x - mean)**2)/(2*(standard_deviation**2)))
 z = z/(np.sqrt(2*np.pi)*standard_deviation);
 return (x, y, z);

# 具体函数方法可用 help(function) 查看，如：help(ax.plot_surface)
x1, y1, z1 = build_layer(0.2);
ax.plot_surface(x1, y1, z1, rstride=1, cstride=1, color='green')

x5, y5, z5 = build_layer(0.15);
ax.plot_surface(x5, y5, z5, rstride=1, cstride=1, color='pink')

# x2, y2, z2 = build_layer(-0.26);
# ax.plot_surface(x2, y2, z2, rstride=1, cstride=1, color='yellow')
#
# x6, y6, z6 = build_layer(-0.22);
# ax.plot_surface(x6, y6, z6, rstride=1, cstride=1, color='pink')

# x4, y4, z4 = build_layer(0);
# ax.plot_surface(x4, y4, z4, rstride=1, cstride=1, color='purple')

x3, y3, z3 = build_gaussian_layer(0, 1)
ax.plot_surface(x3, y3, z3, rstride=1, cstride=1, cmap='rainbow')
plt.show()

这是第三张图片的代码

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d

x, y = np.mgrid[-1:1:20j, -1:1:20j]
z = x * np.exp(-x ** 2 - y ** 2)

ax = plt.subplot(111, projection='3d')
ax.plot_surface(x, y, z, rstride=2, cstride=1, cmap=plt.cm.coolwarm, alpha=0.8)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

plt.show()

以上这篇使用python绘制3维正态分布图的方法就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • python高斯分布概率密度函数的使用详解

    如下所示: import matplotlib.pyplot as plt import numpy as np from scipy import stats from matplotlib import style style.use('fivethirtyeight') mu_params = [-1, 0, 1] sd_params = [0.5, 1, 1.5] x = np.linspace(-7, 7, 100) f, ax = plt.subplots(len(mu_params

  • Python数据可视化实现正态分布（高斯分布）

    正态分布(Normal distribution)又成为高斯分布(Gaussian distribution) 若随机变量X服从一个数学期望为.标准方差为的高斯分布,记为: 则其概率密度函数为: 正态分布的期望值决定了其位置,其标准差决定了分布的幅度.因其曲线呈钟形,因此人们又经常称之为钟形曲线.我们通常所说的标准正态分布是的正态分布: 概率密度函数 代码实现: # Python实现正态分布 # 绘制正态分布概率密度函数 u = 0 # 均值μ u01 = -2 sig = math.sqrt(

  • Python绘制频率分布直方图的示例

    项目中在前期经常要看下数据的分布情况,这对于探究数据规律非常有用.概率分布表示样本数据的模样,长的好不好看如果有图像展示出来就非常完美了,使用Python绘制频率分布直方图非常简洁,因为用的频次非常高,这里记录下来.还是Python大法好,代码简洁不拖沓~ 如果数据取值的范围跨度不大,可以使用等宽区间来展示直方图,这也是最常见的一种:如果数据取值范围比较野,也可以自定义区间端点,绘制图像,下面分两种情况展示 1. 区间长度相同绘制直方图 #-*- encoding=utf-8 -*- impor

  • 在python中画正态分布图像的实例

    1.正态分布简介 正态分布(normal distribtution)又叫做高斯分布(Gaussian distribution),是一个非常重要也非常常见的连续概率分布.正态分布大家也都非常熟悉,下面做一些简单的介绍. 假设随机变量XX服从一个位置参数为μμ.尺度参数为σσ的正态分布,则可以记为: 而概率密度函数为 2.在python中画正态分布直方图 先直接上代码 import numpy as np import matplotlib.mlab as mlab import matplot

  • Python并行分布式框架Celery详解

    Python并行分布式框架Celery详解

    Celery 简介 除了redis,还可以使用另外一个神器---Celery.Celery是一个异步任务的调度工具. Celery 是 Distributed Task Queue,分布式任务队列,分布式决定了可以有多个 worker 的存在,队列表示其是异步操作,即存在一个产生任务提出需求的工头,和一群等着被分配工作的码农. 在 Python 中定义 Celery 的时候,我们要引入 Broker,中文翻译过来就是"中间人"的意思,在这里 Broker 起到一个中间人的角色.在工头提

  • 基于python进行抽样分布描述及实践详解

    基于python进行抽样分布描述及实践详解

    本次选取泰坦尼克号的数据,利用python进行抽样分布描述及实践. 备注:数据集的原始数据是泰坦尼克号的数据,本次截取了其中的一部分数据进行学习.Age:年龄,指登船者的年龄.Fare:价格,指船票价格.Embark:登船的港口. 1.按照港口分类,使用python求出各类港口数据 年龄.车票价格的统计量(均值.方差.标准差.变异系数等). import pandas as pd df = pd.read_excel('/Users/Downloads/data.xlsx',usecols =

  • python分布式编程实现过程解析

    分布式编程的难点在于: 1.服务器之间的通信,主节点如何了解从节点的执行进度,并在从节点之间进行负载均衡和任务调度: 2.如何让多个服务器上的进程访问同一资源的不同部分进行执行 第一部分涉及到网络编程的底层细节 第二个问题让我联想到hdfs的一些功能. 首先分布式进程还是解决的是单机单进程无法处理的大数据量大计算量的问题,希望能加通过一份代码(最多主+从两份)来并行执行一个大任务. 这就面临两个问题,首先将程序分布到多台服务器,其次将输入数据分配给多台服务器. 第一个问题相对比较简单,毕竟程序一

  • Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    本文实例讲述了Python使用numpy产生正态分布随机数的向量或矩阵操作.分享给大家供大家参考,具体如下: 简单来说,正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学.物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力.一般的正态分布可以通过标准正态分布配合数学期望向量和协方差矩阵得到.如下代码,可以得到满足一维和二维正态分布的样本. 示例1(一维正态分布): # coding=utf-8 '''

  • 使用python绘制3维正态分布图的方法

    今天使用python画了几个好玩的3D展示图,现在分享给大家. 先贴上图片 使用的python工具包为: from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D 在贴代码之前,有必要从整体上了解这些图是如何画出来的.可以把上面每一个3D图片理解成一个长方体.输入数据是三维的,x轴y轴和z轴.在第三个图片里面有x.y和z坐标的标识.在第三张图片中,我们可以理解为,

  • python绘制散点图和折线图的方法

    python绘制散点图和折线图的方法

    本文实例为大家分享了python绘制散点图和折线图的具体代码,供大家参考,具体内容如下 #散点图,一般和相关分析.回归分析结合使用 import pandas import matplotlib import matplotlib.pyplot as plt   plot_circle=pandas.read_csv('D://Python projects//reference data//6.1//data.csv') #定义主题颜色 maincolor=(47/256,82/256,141

  • python绘制直方图和密度图的实例

    对于pandas的dataframe,绘制直方图方法如下: //pdf是pandas的dataframe, delta_time是其中一列 //xlim是x轴的范围,bins是分桶个数 pdf.delta_time.plot(kind='hist', xlim=(-50,300), bins=500) 对于pandas的dataframe,绘制概率密度图方法如下: //pdf是pandas的dataframe, delta_time是其中一列 pdf.delta_time.dropna().pl

  • Python绘制二维曲线的日常应用详解

    使用Python绘制出类似Excel或者MATLAB的曲线还是比较容易就能够实现的,需要用到的额外库有两个,numpy和matplotlib.使用这两个模块实现的曲线绘制其实在一定程度上更像是MATLAB的plot功能,不过今天看了一下matplotlib网站上的信息,现在的功能更为强劲了,而且已经支持三维图像的绘制. 模块库的安装非常简单,我使用的Mac,在Mac上用pip进行了两个模块库的安装都十分顺畅.相信其他平台基本上也都这样,如果能够联网,这种安装方式是十分推荐的,确实是简单. 我用P

  • 使用python绘制二维图形示例

    我就废话不多说了,直接上代码吧! import matplotlib.pyplot as plt #也可以使用 import pylab as pl import matplotlib.font_manager as fm myfont = fm.FontProperties(fname=r'C:\Windows\Fonts\simkai.ttf') #或许字体,为设置中文显示 x = [1,2,3,4,5,6] data1 = [1,1.3,1.39,1.41,1.42,1.40] data2

  • python 画3维轨迹图并进行比较的实例

    一. 数据的格式 首先我们需要x,y,z三个数据进行画图.从本实验用到的数据集KITTI 00.txt中举例: 1.000000e+00 9.043680e-12 2.326809e-11 5.551115e-17 9.043683e-12 1.000000e+00 2.392370e-10 3.330669e-16 2.326810e-11 2.392370e-10 9.999999e-01 -4.440892e-16 一组有12个数据,相当于T={R,t},R是3×3的矩阵,t是3×1的矩阵

  • 使用Python绘制空气质量日历图

    使用Python绘制空气质量日历图

    目录 前言 数据 calmap 最后 前言 在github中经常可以看到下面的日历图,可以用来表示每一天在github上的活跃程度. 类似的方法也可以用到空气质量的可视化方式中来,只要有每天的空气质量指数就可以. 数据 我这里使用的是2020年北京市各个监测站点的空气质量观测数据,原始数据包含PM2.5,PM10,AQI指数,这里选择AQI作为示例. 这里对原始数据做了简单处理,具体过程不赘述,感兴趣的话也可以看文末获取方式. 处理后的数据形式如下: calmap 绘制日历图可以用calmap库

  • 利用Python绘制好看的玫瑰花图

    利用Python绘制好看的玫瑰花图

    目录 一.基本极坐标图 二.极半径图 参数介绍 三.画玫瑰花图 AngleAxisOpts参数介绍: TooltipOpts参数介绍: 开始画玫瑰花图 今天主要给大家介绍如何用pyecharts画各种漂亮的数学图形 一.基本极坐标图 说简单点,基本极坐标图就是圆形的散点图(柱状图或折线图),代码如下: import random from pyecharts import options as opts from pyecharts.charts import Polar data = [(i,

  • Python绘制散点密度图的三种方式详解

    Python绘制散点密度图的三种方式详解

    目录 方式一 方式二 方式三 方式一 import matplotlib.pyplot as plt import numpy as np from scipy.stats import gaussian_kde from mpl_toolkits.axes_grid1 import make_axes_locatable from matplotlib import rcParams config = {"font.family":'Times New Roman',"fo

  • Python绘制交通流折线图详情

    Python绘制交通流折线图详情

    目录 一.数据集下载 二.折线图绘制 1.解压npz文件 2.折线图绘制 一.数据集下载 加州高速公路PEMS数据集 这里绘制PEMS04中的交通流量数据.该数据集中包含旧金山2018年1月1日至2月28日的29条道路上307个探测器每五分钟收集的数据. 二.折线图绘制 1.解压npz文件 npz是一种numpy文件存储的压缩格式,可使用numpy进行读取. allow_pickle=True用于防止numpy版本过高带来的错误. data.files查看压缩文件下的所有文件. import n

随机推荐