Python和Matlab实现蝙蝠算法的示例代码

目录

• 1前言
• 2 蝙蝠算法原理细讲
• 3 详细步骤
• 4Python实现
• 4.1代码
• 4.2结果
• 5Matlab实现
• 5.1 代码
• 5.2 结果
• 5.3 展望

1 前言

蝙蝠算法是2010年杨教授基于群体智能提出的启发式搜索算法，是一种搜索全局最优解的有效方法。该算法基于迭代优化，初始化为一组随机解，然后迭代搜寻最优解，且在最优解周围通过随机飞行产生局部新解，加强局部搜索速度。该算法具有实现简单、参数少等特点。

该算法主要用于目标函数寻优，基于蝙蝠种群利用产生的声波搜索猎物和控制飞行方向的特征来实现函数的寻优。以一只蝙蝠作为基本单元，且每只蝙蝠都有一个适应值来对函数解空间进行优化。每只蝙蝠可以调整自身发射声波的响度、频率等对空间进行搜索，使整个种群的活动逐步由无序变为有序。但蝙蝠算法在寻优末段容易陷入局部的极值，本文引入变速度权重因子修正系数(和粒子群参数调整的自适应过程相似)，尽可能避免局部极值的困境，从而达到全局寻优的效果。

2 蝙蝠算法原理细讲

首先在自变量范围内产生蝙蝠的随机位置；

然后每个蝙蝠向周围某处移动，飞行靠声波反馈来更变方向，又向周围移动是随机的，蝙蝠下一时刻移动到某一位置有一定的出现频率，所以本文在运动公式中加了声波和频率两个因素。每一时刻的位移看作是一次飞行，每次飞行的距离很短（距离长短反映出搜素精度）。

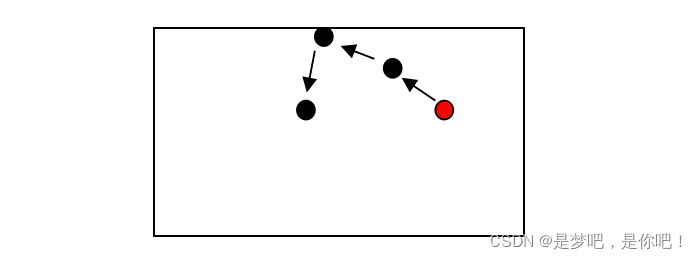
每只蝙蝠初始位置是随机的，在初始位置时刻其中一只蝙蝠对应的函数最值，算法开始会记录该位置，然后所有蝙蝠逐渐向该位置靠近，飞行方向大致向当前最值方向（即该方向的位置该蝙蝠的出现频率更高），但是在飞行方向也是随机飞行的，相当于逐步搜索过去。蝙蝠飞行过程中不会因为当前飞行出现的最大值位置而改变种群的飞行趋势，这样可以尽量避免算法陷入局部极值。

算法每飞行一次就记录一次种群所处位置的最值，最后找出记录中的最值。

算法有两个参数可以影响最终的结果：种群数量和飞行次数。其中种群数量的影响是最大的。 

3 详细步骤

3.1 初始化相关参数

蝙蝠的位置为Xi，飞行速度Vi，声音响度为Ai，频率yi范围，设有目标函数为 ：

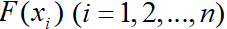
3.2 更改脉冲频率产生的解并更变蝙蝠位置与飞行速度

蝙蝠i在t-1时的位置和飞行速度分别表示为和，群体当前找到的最优位置为。接着根据自身发出不同的音响搜寻猎物，通过接受反馈信息来调整位置xi和飞行速度v(i)。其飞行的速度更变公式如下：

w(t)其中为时刻变速惯性权重因子，作用是使蝙蝠的前期搜索对后期搜索提供参照，wmax为w(t)的最大值、wmin为w(t)的最小值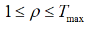；，一般取2，Tmax为最大迭代次数；为当前位置最优解；y(i)为频率满足正态均匀分布的一个随机数，β是一个随机变量，且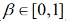。开始运行时，蝙蝠在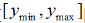随机进行频率分配。

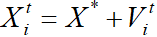
为控制蝙蝠所处位置在自变量范围内，本文针对该情况设置了边界规则：如果下次运动的位置超出了自变量范围，那么下次飞行的位置为投影在的边界上的位置。

3.3 搜寻局部最优解

3.4 通过蝙蝠多次飞行产生多个新解，进行全局搜索，若得到的新解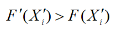

那么接受该解。

3.5 排列所有蝙蝠的位置，并找出当前最优值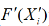及对应的位置

3.6 设当前最优解为，然后使所有蝙蝠继续向下一时刻运动，并返回步骤2重新计算。

3.7 时刻结束，输出:最优解

4 Python实现

4.1 代码

#=========导入相关库===============
import numpy as np
from numpy.random import random as rand

#========参数设置==============
# objfun:目标函数
# N_pop: 种群规模，通常为10到40
# N_gen: 迭代数
# A: 响度（恒定或降低）
# r: 脉冲率（恒定或减小）
# 此频率范围决定范围
# 如有必要，应更改这些值
# Qmin: 频率最小值
# Qmax: 频率最大值
# d: 维度
# lower: 下界
# upper: 上界

def bat_algorithm(objfun, N_pop=20, N_gen=1000, A=0.5, r=0.5,
    Qmin=0, Qmax=2, d=10, lower=-2, upper=2):

    N_iter = 0 # Total number of function evaluations

    #=====速度上下限================
    Lower_bound = lower * np.ones((1,d))
    Upper_bound = upper * np.ones((1,d))

    Q = np.zeros((N_pop, 1)) # 频率
    v = np.zeros((N_pop, d)) # 速度
    S = np.zeros((N_pop, d))

    #=====初始化种群、初始解=======
    # Sol = np.random.uniform(Lower_bound, Upper_bound, (N_pop, d))
    # Fitness = objfun(Sol)
    Sol = np.zeros((N_pop, d))
    Fitness = np.zeros((N_pop, 1))
    for i in range(N_pop):
        Sol[i] = np.random.uniform(Lower_bound, Upper_bound, (1, d))
        Fitness[i] = objfun(Sol[i])

    #====找出初始最优解===========
    fmin = min(Fitness)
    Index = list(Fitness).index(fmin)
    best = Sol[Index]

    #======开始迭代=======
    for t in range(N_gen):

        #====对所有蝙蝠/解决方案进行循环 ======
        for i in range(N_pop):
            # Q[i] = Qmin + (Qmin - Qmax) * np.random.rand
            Q[i] = np.random.uniform(Qmin, Qmax)
            v[i] = v[i] + (Sol[i] - best) * Q[i]
            S[i] = Sol[i] + v[i]

            #===应用简单的界限/限制====
            Sol[i] = simplebounds(Sol[i], Lower_bound, Upper_bound)
            # Pulse rate
            if rand() > r:
                # The factor 0.001 limits the step sizes of random walks
                S[i] = best + 0.001*np.random.randn(1, d)

            #====评估新的解决方案 ===========
            # print(i)
            Fnew = objfun(S[i])
            #====如果解决方案有所改进，或者声音不太大，请更新====
            if (Fnew <= Fitness[i]) and (rand() < A):
                Sol[i] = S[i]
                Fitness[i] = Fnew

            #====更新当前的最佳解决方案======
            if Fnew <= fmin:
                best = S[i]
                fmin = Fnew

        N_iter = N_iter + N_pop

    print('Number of evaluations: ', N_iter)
    print("Best = ", best, '\n fmin = ', fmin)

    return best

def simplebounds(s, Lower_bound, Upper_bound):

    Index = s > Lower_bound
    s = Index * s + ~Index * Lower_bound
    Index = s < Upper_bound
    s = Index * s + ~Index * Upper_bound

    return s

#====目标函数=============
def test_function(u):
    a = u ** 2
    return a.sum(axis=0)

if __name__ == '__main__':
    # print(bat_algorithm(test_function))
    bat_algorithm(test_function)

4.2 结果

5 Matlab实现

5.1 代码

clear
wmax=0.9;%惯性权重最大值
wmin=0.4;%惯性权重最小值
n=10000; % 群体大小
A=rand(1,n); % 声音响度 (不变或者减小)
%% 频率范围
Qmin=0; % 最低频率
Qmax=1; % 最高频率
d=2;% 搜索变量的维数（即频率和速度）
%% 初始矩阵
Q=zeros(n,1); % 频率矩阵初始化
v=zeros(n,d); % 速度矩阵初始化，初始化意义就是产生一个初始矩阵
%% x自变量范围
u=-3;
o=12.1;
% y自变量范围
p=4.1;
l=5.8;
%% 初始化群体/解
for i=1:n
    Sol(i,1)=-3+(12.1+3)*rand(1,1);%x自变量范围【-3，12.1】
    Sol(i,2)=4.1+(5.8-4.1)*rand(1,1);%y自变量【4.1，5.8范围】
    %将随机生成的两个自变量带入函数式
    Fitness(i)=Fun(Sol(i,:));%函数值
end
%% 寻找当前最优解
[fmax,I]=max(Fitness);
best=Sol(I,:);
T=100;%飞行次数
%% 开始飞行
for t=1:T
    for i=1:n,
        Q(i)=Qmin+(Qmin-Qmax)*rand;%rand均匀分布的随机数
        %v(i,:)=v(i,:)+(Sol(i,:)-best)*Q(i);（原速度）
        w=(wmax-wmin)*exp(-2*(t/T)^2)+wmin;%惯性权重因子
        v(i,:)=w*v(i,:)+(Sol(i,:)-best)*A(i)*Q(i);%更改后的速度
        S(i,:)=Sol(i,:)+v(i,:);%位置移动
       %% 边界问题，如果下次飞行超出自变量范围外了，那么下次飞行的位置为投影在的边界上的位置
        %x轴
        if S(i,1)>o
            S(i,1)=o;
        end
        if S(i,1)<u
            S(i,1)=u;
        end
        %y轴
        if S(i,2)>l
            S(i,2)=l;
        end
        if S(i,2)<p
            S(i,2)=p;
        end
        %% 评估该次飞行后产生的新解
        Fnew(i)=Fun(S(i,:));
    end
    [Fmax,Z]=max(Fnew);%找出该次飞行后产生的最大值
    C(t,:)=S(Z,:);
    FFnew(t)=Fmax;
end
[Ffmax,N]=max(FFnew);%找出整个飞行过程中的最大值
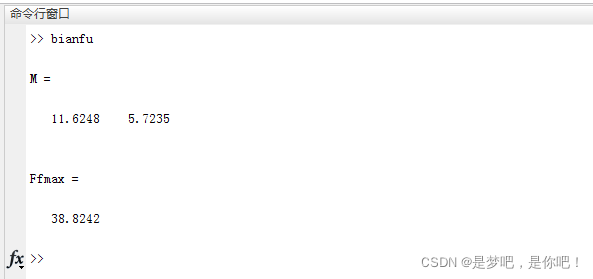
M=C(N,:)
Ffmax

%目标函数
function z=Fun(u)
   z=21.5+u(1)*sin(4*pi*u(1))+u(2)*sin(20*pi*u(2));

5.2 结果

5.3 展望

如果是其他函数怎么办呢？

函数z=21.5+u(1)*sin(4*pi*u(1))+u(2)*sin(20*pi*u(2))中的两个自变量对应程序中的是Sol(i,1)=-3+(12.1+3)*rand(1,1);%x自变量范围【-3，12.1】和Sol(i,2)=4.1+(5.8-4.1)*rand(1,1);%y自变量【4.1，5.8范围】，两自变量产生的是列矩阵，而程序中Sol(i,:) 提取的是矩阵中的行，所以如果对该函数增减自变量，或者想求其他含有多个自变量的函数，程序中只用修改以下程序部分，其他参数也可以自行更改（注：自变量的范围和个数增加了，那么种群个数和飞行次数务必要增加）：

Sol(i,1)=-3+(12.1+3)*rand(1,1);%x自变量范围【-3，12.1】

Sol(i,2)=4.1+(5.8-4.1)*rand(1,1);%y自变量【4.1，5.8范围】

和

% x自变量范围

u=-3;

o=12.1;

% y自变量范围

p=4.1;

l=5.8;

到此这篇关于Python和Matlab实现蝙蝠算法的示例代码的文章就介绍到这了,更多相关Python和Matlab蝙蝠算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！