java词法分析器DDL递归应用详解

目录

• 前言
• intellij plugin
• 词法解析
• 状态迁移
• DDL 解析
• 递归解析
• 总结

前言

最近大部分时间都在撸Python，其中也会涉及到将数据库表转换为Python中ORM框架的Model，但我们并没有找到一个合适的工具来做这个意义不大的”体力活“，所以每次新建表后大家都是根据自己的表结构手写一遍Model。

一两张表还好，一旦 10 几张表都要写一遍时那痛苦只有自己知道；这时程序员的 slogan 再次印证：一切毫无意义的体力劳动终将被计算机取代。

intellij plugin

既然没有现成的工具那就自己写一个吧，演示效果如下：

考虑到我们主要是用PyCharm开发，正好jetbrains也提供了SDK用于开发插件，所以UI层面可以不用额外考虑了。

使用流程很简单，只需要导入DDL语句就可以生成Python所需要的Model代码。

例如导入以下 DDL：

CREATE TABLE `user` (
  `id` int(11) NOT NULL AUTO_INCREMENT,
  `userName` varchar(20) DEFAULT NULL COMMENT '用户名',
  `password` varchar(100) DEFAULT NULL COMMENT '密码',
  `roleId` int(11) DEFAULT NULL COMMENT '角色ID',
  PRIMARY KEY (`id`),
) ENGINE=InnoDB AUTO_INCREMENT=7 DEFAULT CHARSET=utf8

便会生成对应的 Python 代码：

class User(db.Model):
    __tablename__ = 'user'
    id = db.Column(db.Integer, primary_key=True, autoincrement=True)
    userName = db.Column(db.String)  # 用户名
    password = db.Column(db.String)  # 密码
    roleId = db.Column(db.Integer)  # 角色ID

词法解析

仔细对比源文件及目标代码会很容易找出规律，无非就是解析出表名、字段、及字段的属性（是否为主键、类型、长度），最后再转换为Python所需要的模板即可。

在我动手之前我认为是非常简单的，无非就是解析字符串，但实际上手后发现不是那么回事；主要是有以下几个问题：

• 如何识别出表名称？
• 同样的如何识别出字段名称，同时还得关联上该字段的类型、长度、注释。
• 如何识别出主键？

总结一句话，如何通过一系列规则识别出一段字符串中的关键信息，这同样也是 MySQL Server 所做的事情。

在开始真正解析 DDL 之前，先来看下一段简单的脚本如何解析：

x = 20

按照我们平时开发的经验，这条语句分为以下几部分：

• x表示变量
• =表示赋值符号
• 20表示赋值结果

所以我们对这段脚本的解析结果应当为：

VAR x

GE =

VAL 100

这个解析过程在编译原理中称为”词法解析“，可能大家听到编译原理这几个字就头大（我也是）；对于刚才那段脚本我们可以编写一个非常简单的词法解析器生成这样的结果。

状态迁移

再开始之前先捋一下思路，可以看到上文的结果中通过VAR表示变量、GE表示赋值符号 ”=“、VAL表示赋值结果，现在需要重点记住这三个状态。

在依次读取字符解析时，程序就是在这几个状态中来回切换，如下图：

• 默认为初始状态。
• 当字符为字母时进入VAR状态。
• 当字符为 ”=“ 符号时进入GE状态。

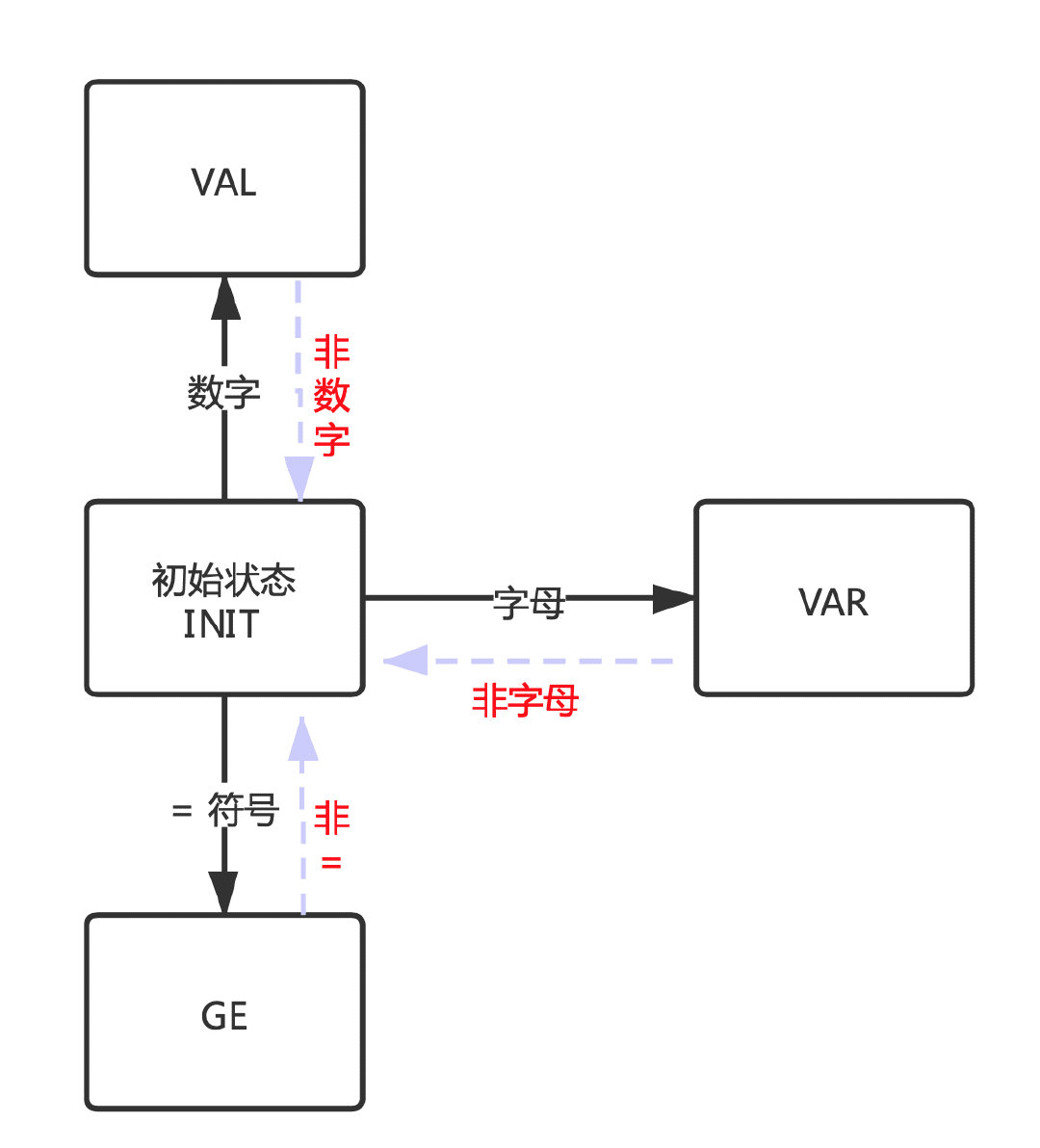
同理，当不满足这几个状态时候又会回到初始从而再次确认新的状态。

光看图有点抽象，直接来看核心代码：

public class Result{
    public TokenType tokenType ;
    public StringBuilder text = new StringBuilder();
}

首先定义了一个结果类，收集最终的解析结果；其中的TokenType就对应了图中的三种状态，简单的用枚举值来表示。

public enum TokenType {
    INIT,
    VAR,
    GE,
    VAL
}

首先对应到第一张图：初始化状态。

需要对当前解析的字符定义一个TokenType：

和图中描述的流程一致，判断当前字符给定一个状态即可。

接着对应到第二张图：状态之间的转换。

会根据不同的状态进入不同的case，在不同的case中判断是否应当跳转到其他状态（进入INIT状态后会重新生成状态）。

举个例子：x = 20:

首选会进入VAR状态，接着下一个字符为空格，自然在 38 行中重新进入初始状态，导致再次确定下一个字符=进入GE状态。

当脚本为ab = 30:
第一个字符为 a 也是进入VAR状态，第二个字符为 b，依然为字母，所以进入 36 行，状态不会改变，同时将 b 这个字符追加进来；后续步骤就和上一个例子一致了。

多说无益，建议大家自己跑一下单测就会明白：

https://github.com/crossoverJie/sqlalchemy-transfer/blob/master/src/test/java/top/crossoverjie/plugin/core/lab/TestLexerTest.java

DDL 解析

简单的解析完成后来看看DDL这样的脚本应当如何解析：

CREATE TABLE `user` (
  `id` int(11) NOT NULL AUTO_INCREMENT,
  `userName` varchar(20) DEFAULT NULL COMMENT '用户名',
  `password` varchar(100) DEFAULT NULL COMMENT '密码',
  `roleId` int(11) DEFAULT NULL COMMENT '角色ID',
  PRIMARY KEY (`id`),
) ENGINE=InnoDB AUTO_INCREMENT=7 DEFAULT CHARSET=utf8

原理类似，首先还是要看出规律（也就是语法）：

• 表名是第一行语句，同时以CREATE TABLE开头。
• 每一个字段的信息（名称、类型、长度、备注）都是以 “`” 符号开头 “,” 结尾。
• 主键是以 PRIMART 字符串开头的字段，以)结尾。

根据我们需要解析的数据种类，我这里定义了这个枚举：

然后在初始化类型时进行判断赋值：

由于需要解析的数据不少，所以这里的判断条件自然也就多了。

递归解析

针对于DDL的语法规则，我们这里还有需要有特殊处理的地方；比如解析具体字段信息时如何关联起来？

举个例子：

`userName` varchar(20) DEFAULT NULL COMMENT '用户名',
`password` varchar(100) DEFAULT NULL COMMENT '密码',

这里我们解析出来的数据得有一个映射关系：

所以我们只能一个字段的全部信息解析完成并且关联好之后才能解析下一个字段。

于是这里我采用了递归的方式进行解析（不一定是最好的，欢迎大家提出更优的方案）。

} else if (value == '`' && pStatus == Status.BASE_INIT) {
    result.tokenType = DDLTokenType.FI;
    result.text.append(value);
}

当当前字符为 ”`“ 符号时，将状态置为 “FI”(FieldInfo)，同时当解析到为 “,” 符号时便进入递归处理。

可以理解为将这一段字符串单独提取出来处理：

`userName` varchar(20) DEFAULT NULL COMMENT '用户名',

接着再将这段字符递归调用当前方法再次进行解析，这时便按照字段名称、类型、长度、注释的规则解析即可。

同时既然存在递归，还需要将子递归的数据关联起来，所以我在返回结果中新增了一个pid的字段，这个也容易理解。

默认值为 0，一旦递归后便自增 +1，保证每次递归的数据都是唯一的。

用同样的方法在解析主键时也是先将整个字符串提取出来:

PRIMARY KEY (`id`)

只不过是 “P” 打头 “)” 结尾。

} else if (value == 'P' && pStatus == Status.BASE_INIT) {
    result.tokenType = DDLTokenType.P_K;
    result.text.append(value);
}

也是将整段字符串递归解析，再递归的过程中进行状态切换P_K ---> P_K_V最终获取到主键。

所以通过对刚才那段DDL解析得到的结果如下：

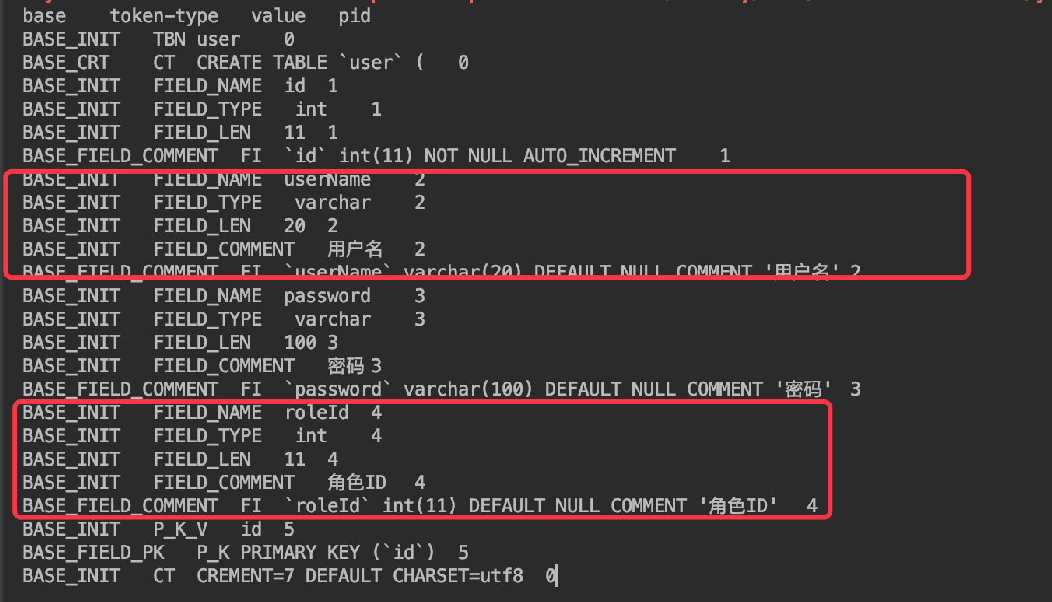
这样每个字段也通过了pid进行了区分关联。

所以现在只需要对这个词法解析器进行封装，便可以提供一个简单的API来获取表中的数据了。

总结

到此整个词法解析器的全部内容都已经完成了，虽然实现的是一个小功能，但我自己花的时间可不少，其中光复习编译原理就让人头疼。

但这还只是整个编译语言知识点的冰山一角，后续还有语法、语义、中间、目标代码等一系列内容，都是一个比一个难啃。

本文所有源码及插件地址：

https://github.com/crossoverJie/sqlalchemy-transfer

以上就是java词法分析器DDL递归应用详解的详细内容，更多关于java DDL递归词法分析器的资料请关注我们其它相关文章！