C++实例分析组合数的计算与排列组合的产生

目录
  • 组合数的计算
    • 使用加法递推—O(n^2)
    • 使用乘法递推—O(n)
  • 排列和组合的产生(无重集元素)
    • 全排列
    • 一般组合
    • 全组合
    • 由上一排列产生下一排列
    • 由上一组合产生下一组合

组合数的计算

使用加法递推—O(n^2)

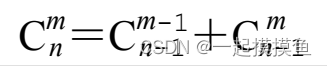
边界条件

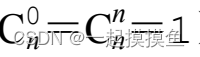
int C[1001][1001]; // 根据实际需要开数组，必要时采用高精度类型
//……
memset(C,0,sizeof(C));
for (int i=0;i<=n;i++)
{
C[i][0]=1;
for (int j=0;j<=i;j++)
C[i][j]=C[i-1][j-1] + C[i-1][j];
}

使用乘法递推—O(n)

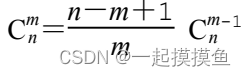
边界条件

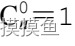
必须先乘后除，否则除不开

一个小优化：

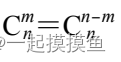
（m＞n/2时用）

int C[1001]; // C[m]其实表示C[n][m]，必要时采用高精度类型
……
C[0]=1;
if (m>n-m) m=n-m;
for (int i=1;i<=m;i++)
C[i] = (n-i+1) * C[i-1] / i; // 如果怕溢出，可以把中间结果转化成long long。

排列和组合的产生(无重集元素)

int item[N]; // 第i位要放置的数字
bool used[N];
int n,m;

全排列

将 n 个数字 1～n 进行排序，有多少种排序方法？

使用深度优先搜索，对 n 个位置逐个进行试探。时间复杂度为 O(n!)。

void full_ permutation(int depth)
{
if (depth==n)
{
// print(); // 输出结果
return;
}
for (int i=0; i<n; i++)
if (!used[i])
{
used[i]=true;
item[depth]=i+1;
try(depth+1);
used[i]=false; // 别忘记清除”使用”标记
}
}

一般组合

从 n 个元素 1～n 中任取 m 个元素，有多少种取法？

一个合法的组合有这样一个特点：排在右面的数字一定严格大于左面的数字。比如说某一位上取了 3，那么从 4 开始搜索下一位就可以了。

void combination(int depth, int p)
{
if (depth==m)
{
// print(); // 输出结果
return;
}
for (int i=p+1 ; i<n-(m-depth) ; i++)
{
// 由于后面的元素一定前面的大，所以不需要标记used了。
item[depth]=i;
try(depth+1);
}
}
combination(0,0);

全组合

输入 n 个数，求这 n 个数构成的集合的所有非空子集。

和一般组合不同，这次只要产生一个解，就马上输出。

void full_combination(int l, int p)
{
for (int i=0; i<l; i++) // 每次进入递归函数都输出
cout<<item[i]<<" ";
cout<<endl;
for (int i=p; i<n; i++)
{
item[l] = i; // 在l位置放上该数
full_combination(l+1, i+1); // 填下一个位置
}
}
full_combination(0, 0);

注意：对于一个整数，每一位不是 0 就是 1，所以可以用整数来表示一个集合。具体实例可参见 “2.8Healthy Holsteins”。

由上一排列产生下一排列

① 从右往左寻找第一个小于右边的数，位置为 j。

② 在 j 位置的右边寻找大于 aj的最小数字 ak（位置 k）

③ 将 aj 与 ak的值进行交换

④ 将数列的 j+1 位到 n 位倒转。

int a[N]; // 初始化：a[i]是字典序最小的排列, 0≤i＜N
int j,k, p,q, temp;
j=(n-1) - 1;
while ((j>=0)&&(a[j]>a[j+1])) j--; // 从右往左寻找第一个小于右边的数，位置为j。
if (j>=0) // 如果j<0说明已经排完了。
{
k=n-1;
while (a[k]<a[j]) k--; // 在j位置的右边寻找大于aj的最小数字ak（位置k）
swap(a[j], a[k]); // 将aj与ak的值进行交换
for (p=j+1,q=n-1; p<q; p++,q--) // 将数列的j+1位到n位倒转
swap(a[p], a[q]);
}

STL 中有与此相同的算法。头文件为<algorithm>。

next_permutation(序列第一项的地址, 序列最后一项的地址+1)：产生下一排列。

prev_permutation(序列第一项的地址, 序列最后一项的地址+1)：产生上一排列。

这两个函数能够用于可重集的排列。

由上一组合产生下一组合

① 从右向左寻找可以往下取一个元素的数，位置为 j。

（举个例子：从 7 个数中取 4 个数，有一个组合为 1367，那么 6、7 就不能再往下取了）

② 数列的 j 位到 n 位重新取元素。

注意：

① 从 N 个连续元素中取 M 个元素。如果元素序号不连续，就需要修改下面的“+1”。

② 右侧的数字一定严格大于左侧的数字。

int a[M]; // 初始化：a[i]是字典序最小的排序, 0≤i＜M，1≤a[i]≤N
//……
int j=m-1;
while ((j>=0)&&(a[j]==n-(m-1 -j))) j--;
if (i>=0)
{
a[j]++;
for (int k=j+1; k<m; k++) a[k]=a[k-1]+1;
}

到此这篇关于C++实例分析组合数的计算与排列组合的产生的文章就介绍到这了,更多相关C++组合数的计算内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • C/C++中组合详解及其作用介绍

    C/C++中组合详解及其作用介绍

    目录 概述 案例 总结 概述 组合 (Composition) 指在一个类中另一类的对象作为数据成员. 案例 在平面上两点连成一条直线, 求直线的长度和直线中点的坐标. 要求: 基类: Dot 派生类: Line (同时组合) 派生类 Line 从基类 Dot 继承的 Dot 数据, 存放直线的中点坐标 Line 类再增加两个 Dot 对象, 分别存放两个端点的坐标 Dot 类: #ifndef PROJECT5_DOT_H #define PROJECT5_DOT_H #include <io

  • C++实现数组中元素组合出最大值

    C++实现数组中元素组合出最大值

    目录 数组中元素组合出最大值 如题:这可以算是一个算法类 数组或vector求最大值最小值 1.求数组的最大值或最小值 2.求数组最大值最小值对应的下标 数组中元素组合出最大值 如题:这可以算是一个算法类 class Solution { public: string largestNumber(vector<int>& nums) { string res; sort(nums.begin(), nums.end(), [](const int& x, const int&a

  • C++中求组合数的各种方法总结详解

    [问题]      组合问题 问题描述:找出从自然数1.2.... .n中任取r个数的所有组合.例如n=5,r=3的所有组合为: 1,2,31,2,4 1,3,4 2,3,4 1,2,5 1,3,5 2,3,5 1,4,5 2,4,5 3,4,5 用程序实现有几种方法: 1)穷举法 程序如下[程序]#include<stdio.h>const int n=5,r=3;int    i,j,k,counts=0; int main(){     for(i=1;i<=r ;i++)    

  • C++实现LeetCode(179.最大组合数)

    [LeetCode] 179. Largest Number 最大组合数 Given a list of non negative integers, arrange them such that they form the largest number. Example 1: Input: [10,2] Output: "210" Example 2: Input: [3,30,34,5,9] Output: "9534330" Note: The result

  • C++实现LeetCode(46.全排列)

    [LeetCode] 46. Permutations 全排列 Given a collection of distinct integers, return all possible permutations. Example: Input: [1,2,3] Output: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] 这道题是求全排列问题,给的输入数组没有重复项,这跟之前的那道 Combinations 和类似,解法基本相同

  • C++实现LeetCode(47.全排列之二)

    [LeetCode] 47. Permutations II 全排列之二 Given a collection of numbers that might contain duplicates, return all possible unique permutations. Example: Input: [1,1,2] Output: [ [1,1,2], [1,2,1], [2,1,1] ] 这道题是之前那道 Permutations 的延伸,由于输入数组有可能出现重复数字,如果按照之前的

  • 使用C++实现全排列算法的方法详解

    使用C++实现全排列算法的方法详解

    复制代码 代码如下: <P>不论是哪种全排列生成算法,都遵循着"原排列"→"原中介数"→"新中介数"→"新排列"的过程.</P><P>其中中介数依据算法的不同会的到递增进位制数和递减进位制数.</P><P>关于排列和中介数的一一对应性的证明我们不做讨论,这里仅仅给出了排列和中介数的详细映射方法.</P> · 递增进位制和递减进位制数  所谓递增进位制和递减

  • C++简单实现的全排列算法示例

    本文实例讲述了C++简单实现的全排列算法.分享给大家供大家参考,具体如下: #include "stdafx.h" #include <string> #include <algorithm> #include <iostream> void func(const char *str_in) { std::string str(str_in); std::sort(str.begin(),str.end()); do { std::cout<&

  • C++实例分析组合数的计算与排列组合的产生

    C++实例分析组合数的计算与排列组合的产生

    目录 组合数的计算 使用加法递推—O(n^2) 使用乘法递推—O(n) 排列和组合的产生(无重集元素) 全排列 一般组合 全组合 由上一排列产生下一排列 由上一组合产生下一组合 组合数的计算 使用加法递推—O(n^2) 边界条件 int C[1001][1001]; // 根据实际需要开数组,必要时采用高精度类型 //-- memset(C,0,sizeof(C)); for (int i=0;i<=n;i++) { C[i][0]=1; for (int j=0;j<=i;j++) C[i]

  • PHP计算日期相差天数实例分析

    本文实例分析了PHP计算日期相差天数的方法.分享给大家供大家参考,具体如下: <?PHP //今天与2016年10月27日相差多少天 $Date_1=date("Y-m-d"); $Date_2="2016-10-27"; $d1=strtotime($Date_1); $d2=strtotime($Date_2); $Days=round(($d1-$d2)/3600/24); echo "今天与2016年10月27日相差".$Days.

  • Python实现的排列组合计算操作示例

    Python实现的排列组合计算操作示例

    本文实例讲述了Python实现的排列组合计算操作.分享给大家供大家参考,具体如下: 1. 调用 scipy 计算排列组合的具体数值 >> from scipy.special import comb, perm >> perm(3, 2) 6.0 >> comb(3, 2) 3.0 2. 调用 itertools 获取排列组合的全部情况数 >> from itertools import combinations, permutations >>

  • C#实现排列组合算法完整实例

    排列组合是常见的数学问题,本文就以完整实例形式讲述了C#实现排列组合算法的方法.分享给大家供大家参考之用.具体方法如下: 首先,数学中排列组合,可表示为:排列P(N,R) 其实排列实现了,组合也就实现了,组合C(N,R)就是P(N,R)/P(R,R) ,实现这一功能比较简单的是递归算法,但考虑到递归的性能,下面采用了2种非递归的方法,具体代码如下 using System; using System.Collections.Generic; namespace Test { class Prog

  • JS实现的排列组合算法示例

    JS实现的排列组合算法示例

    本文实例讲述了JS实现的排列组合算法.分享给大家供大家参考,具体如下: 在数学中有排列组合,用来计算概率. 比如:从4个数字中,任意选择两个的情况.从5个数字中任意选择3个数字的情况.(这里我们只考虑没有顺序的情况). 公式:C(n,m)=n!/[m!(n-m)!]=n*(n-1)*...*(n-m+1)/[1*2*...*m],如C(5,2)=[5*4]/[1*2]=10. 举例说明:有 1,2,3,4 四个数字,从这四个数字中,任意选择两个数字一共有多少种情况:[1,2], [1,3], [

  • js实现简单排列组合的方法

    js实现简单排列组合的方法

    本文实例讲述了js实现简单排列组合的方法.分享给大家供大家参考,具体如下: 运行效果截图如下: 具体代码如下: <!DOCTYPE html> <html> <head> <title>demo</title> <script type="text/javascript"> var str = [1,2,3,4,5]; var count = 0; function arrange(s){ for(var i=0,

  • Python列表list排列组合操作示例

    本文实例讲述了Python列表list排列组合操作.分享给大家供大家参考,具体如下: 排列 例如: 输入为 ['1','2','3']和3 输出为 ['111','112','113','121','122','123','131','132','133','211','212','213','221','222','223','231','232','233','311','312','313','321','322','323','331','332','333'] 实现代码: # -*-

  • Python实现的排列组合、破解密码算法示例

    本文实例讲述了Python实现的排列组合.破解密码算法.分享给大家供大家参考,具体如下: 排列组合(破解密码) 1.排列 itertools.permutations(iterable,n) 参数一:要排列的序列, 参数二:要选取的个数 返回的是一个迭代对象,迭代器中的每一个元素都是一个元组 import itertools #概念:从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(Arrangement).特别地,当m=n时,这个排列被称作

  • 高效的java版排列组合算法

    本文实例为大家分享了java排列组合算法的具体代码,供大家参考,具体内容如下 package BeanUtil; import java.util.ArrayList; import java.util.List; import com.work.core.exception.OurException; /** * 统计任三出现的最多的几率的组合 * * @author wangmingjie * @date 2009-1-1下午01:22:19 */ public class Copy_2_o

  • Python计算斗牛游戏概率算法实例分析

    本文实例讲述了Python计算斗牛游戏概率算法.分享给大家供大家参考,具体如下: 过年回家,都会约上亲朋好友聚聚会,会上经常会打麻将,斗地主,斗牛.在这些游戏中,斗牛是最受欢迎的,因为可以很多人一起玩,而且没有技术含量,都是看运气(专业术语是概率). 斗牛的玩法是: 1. 把牌中的JQK都拿出来 2. 每个人发5张牌 3. 如果5张牌中任意三张加在一起是10的 倍数,就是有牛.剩下两张牌的和的10的余数就是牛数. 牌的大小: 4条 > 3条 > 牛十 > 牛九 > -- >

随机推荐