最短时间学会基于C++实现DFS深度优先搜索

目录

• 前言
• 1.迷宫找出口,区分dfs,bfs：
• 一、DFS经典放牌可能组合
• 二、leetcode 员工的重要性
• 三、leetcode 图像渲染
• 四、leetcode 被围绕的区域
• 五、岛屿数量
• 六、 小练习：岛屿的最大面积
• 总结

前言

同学们肯定或多或少的听到过别人提起过DFS，BFS，却一直都不太了解是什么，其实两个各为搜索算法，常见使用 深度优先搜索（DFS） 以及 广度优先搜索（BFS） ，今天我们就来讲讲什么是深度优先搜索，深度优先就是撞到了南墙才知道回头，才会往上一层返回。

1.迷宫找出口,区分dfs,bfs：

dfs: 深度优先我们可以看出他一次只往一个方向走,直到撞到了才会返回上一层去尝试其他结果,图片为上左下右的去走

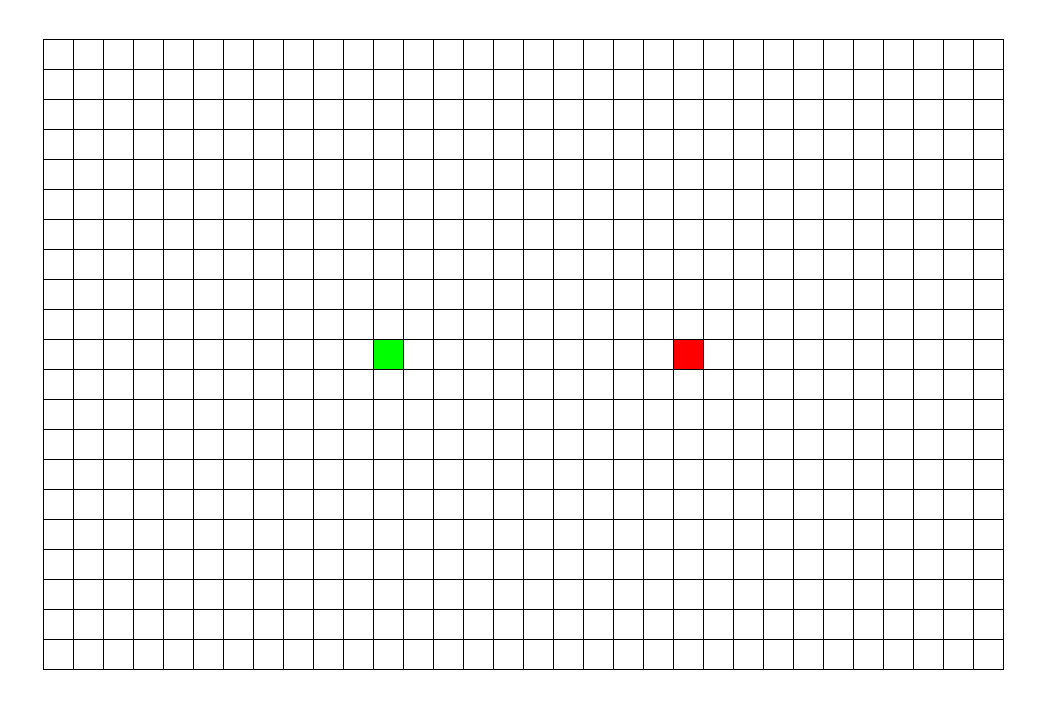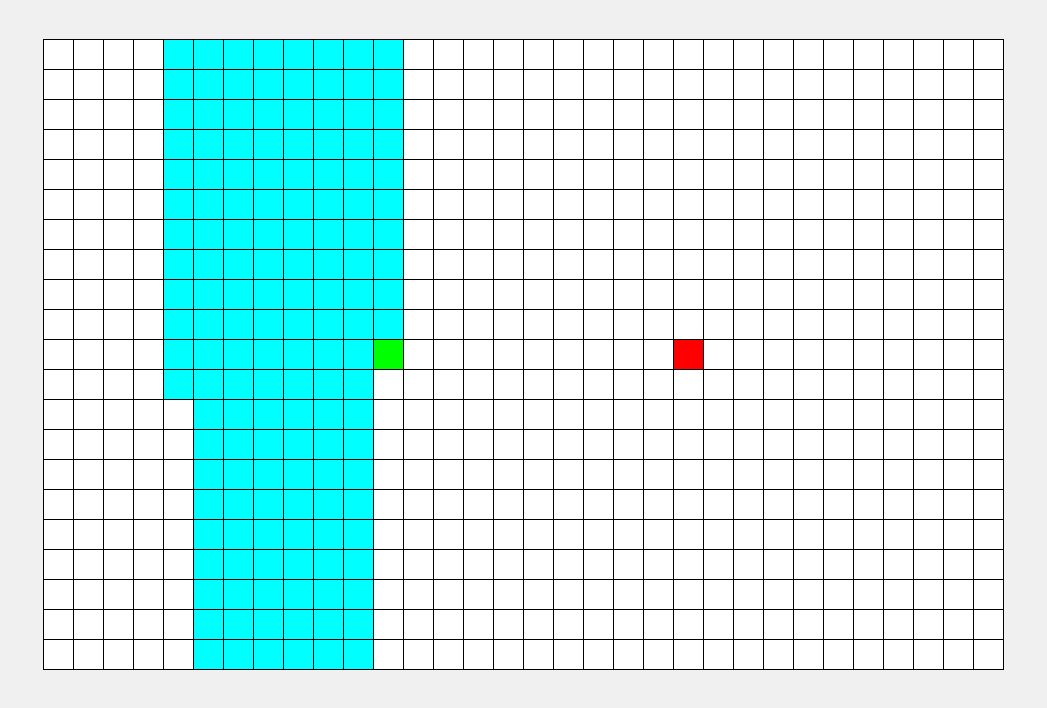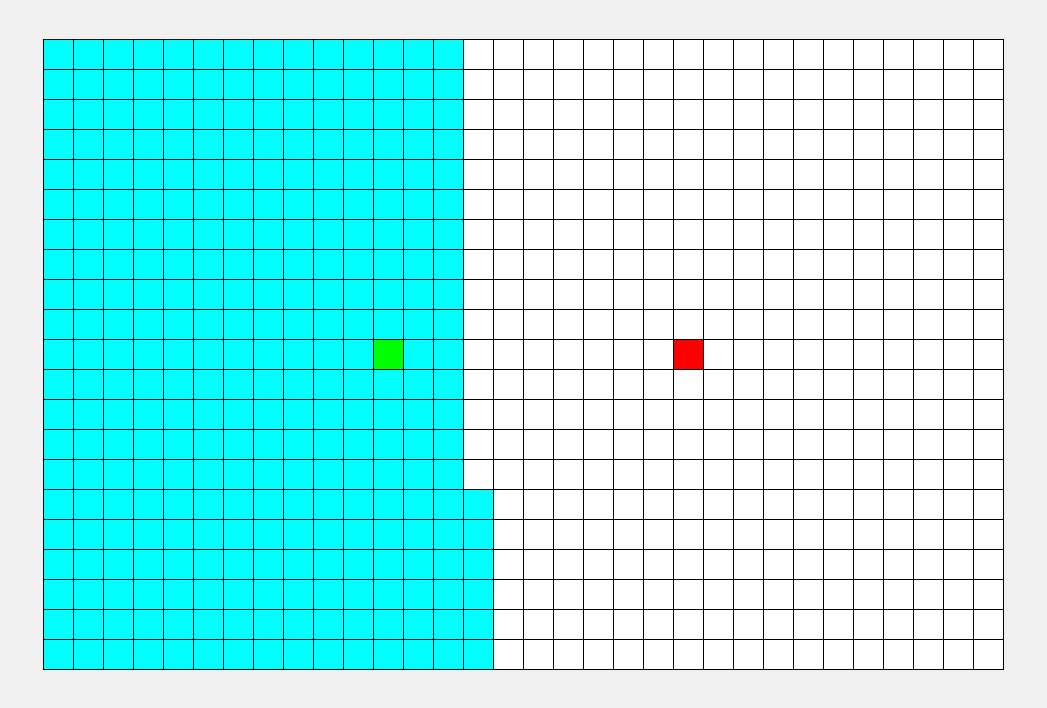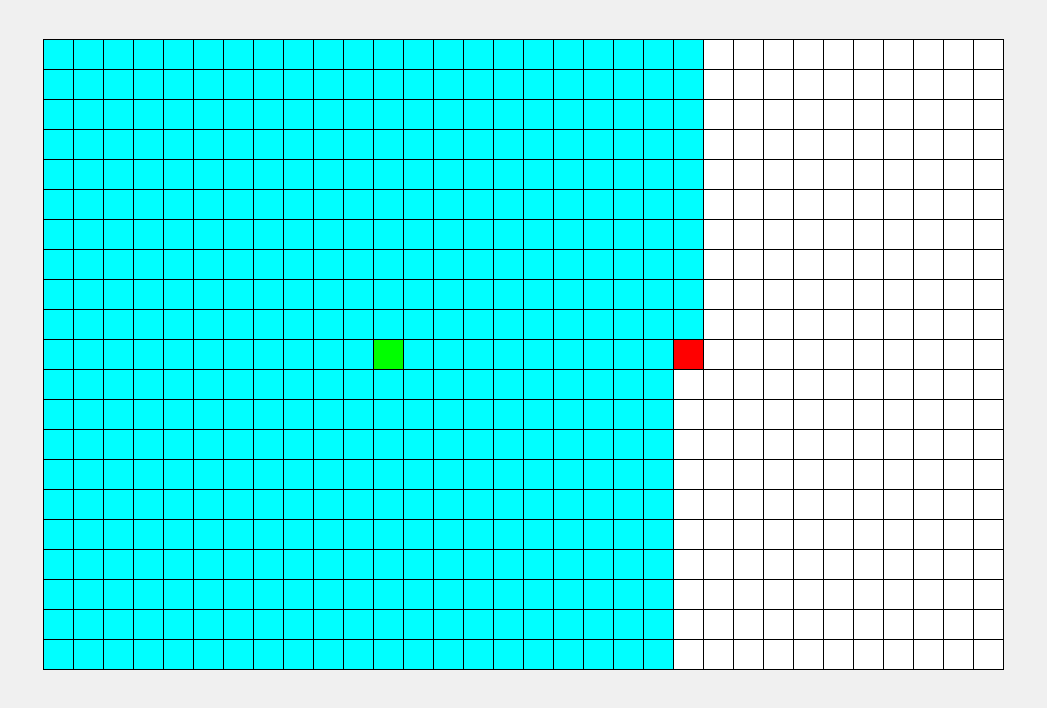
BFS:广度优先就是尝试该位置的旁边的所有可能,再把所有可能的能走到的所有可能继续走.撞到了就停止,如果全部可能都'碰壁'表示从该位置无法走到终点

对比两个遍历方式,相信大家有了初步的认识,让我们接下来看看这道题

一、DFS经典放牌可能组合

题目：我们手上有编号为1~3的三个扑克牌，我们要放到编号为1 ~ 3的盒子当中，并且每个盒子中只放一张牌，问我们有多少种方法。

聪明的同学可能想一想就知道是6种了，但是当我们的要用计算机表达时我们要如何处理呢？题目虽简单,所以我们借这道题来看看DFS如何解题.

方法一： 暴力循环，三层循环嵌套，判断每张牌只用一次,这种方法简单粗暴.

方法二： 深度搜索，我们选择把按照从小到大的依次尝试，在第一个盒子先开始放1，这时我们剩下两张牌，对第二个盒子来说，我们从小到大放，放2，第三个盒子只有3了，第一种放法就出来了 1 2 3。
此时我们全部牌都放完了，然后我们这时候就是撞到了南墙了，我们就开始回收3，回收3的时候如果我们重复放3到第三个盒子就和之前重复了，所以我们再回收2，这时我们就可以把3放到第二个盒子，把2放在第三个盒子，第二种放法就出来了，1 3 2。

这时我们放完了之后再回收，我们回收了2，3后，1的所有可能我们就已经遍历完了，这个时候我们就回收1，这时我们就可以开始把2放到第一个盒子，这时我们还有1 ，3 ，我们按之前的从小到大的原则，把1放入第二个盒子，剩一个3放在第三个盒子，这时的第三种放法 2 1 3出来了

同理我们收两张牌就有组合2 3 1 ，同理3 1 2 ，2 31 ，这样我们的6种出来了，即：我们站在一个盒子，我们按照我们手中的牌，从小到大依次尝试，即我们有一个循环，从第一张牌开始

//处理第index个盒子 _ - - 并行递归，n有多大我们就调用多少次
DFS(vector<int>& box,int index,vector<int>& visited,int n)
{//box为盒子，index为当前盒子，visited为标记哪张牌用了的数组，n为处理几张牌
	if(index == n+1)//每一个盒子都有牌了
	{
		return;
	}
	for(int i =1;i<n;++i)
	{
		if(visited[i]==0)
		{
			//表示没有用过的牌就可以放在当前的盒子当中
			box[index] = i;//当前的盒子放这张牌
			visited[i] =1 ;
			//这里的逻辑就是我们站在一个盒子，我们按照我们手中的牌，从小到大依次尝试
			//到这里我们就处理下一个盒子
			DFS(box,index+1,visited,n);
			//一种方法完成，我们就回收牌
			visited[i]=0;//标记成0就可以再次使用啦！
		}
	}
}

下面这个是测试n张牌，n个盒子的时候，我们所有的可能，可以自行粘贴复制到编辑器当中测试，请自行输入n

void DFS(int index, int n, vector<int>& box, vector<int>& visited)
{
	//处理当前的盒子

	//我们这里打印看看每个盒子装的都是什么
	if (index == n + 1)
	{
		for (int i=1;i<box.size();++i)
			cout << box[i] << " ";
		cout << endl;

		//表示每个盒子我们都已经放满了东西，我们就可以返回上一层
		return;
	}

	//每个盒子都要用n张牌来看看是否能够使用，按照我们从小到大使用的规定原则
	for (int i = 1; i <= n; ++i)
	{
		//表示牌没有被用过，可以使用
		if (visited[i] == 0)
		{
			box[index] = i;//表示在看到index个盒子的时候，我们用第i张牌放入

			visited[i] = 1;//标记当前牌已经被使用
			//走到这里我们当前这个盒子该干的事情已经干完了，我们就可以处理下一个盒子

			DFS(index + 1, n, box, visited);
			//表示所有的牌都已经放入并且返回，这时我们回收牌
			visited[i] = 0;
		}
	}
}
int main()
{
	int n;
	vector<int> box;
	vector<int> vistied;
	cin >> n;
	box.resize(n + 1, 0);
	vistied.resize(n + 1, 0);
	//这里的1是我们当前走到盒子，n是我们有多少牌，boxs是我们用来存放的盒子，
	//visited是用来确定是否访问过的标记矩阵
	DFS(1, n, box, vistied);
	return 0;
}

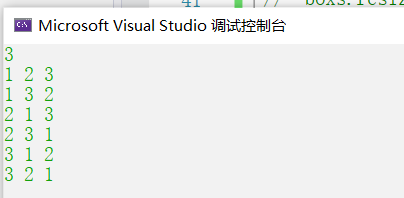
刚开始接触DFS有时候会思考一些奇奇怪怪的问题,这个时候大家应该都去调试调试,一开始的问题一定是要解决的!!!

总结归纳：
深度优先搜索的关键是解决当下应该怎么做，下一步的做法和当下的做法是一样的。当下的做法如何做到尝试每一种可能，我们用for循环遍历，对于每一种可能的确定后，我们继续下一步，当前的可能等到从下一步会退之后再处理
DFS常见的模型:
DFS(当前这一步的逻辑)
{
1.判断边界,是否已经撞到墙了:向上回退
2.尝试当下的每一种可能
3.确定一种可能之后,继续下一步,DFS(下一步)
}

二、leetcode 员工的重要性

员工的重要性

/*
// Definition for Employee.
class Employee {
public:
    int id;
    int importance;
    vector<int> subordinates;
};
*/

class Solution {
public:
    int getImportance(vector<Employee*> employees, int id) {

    }
};

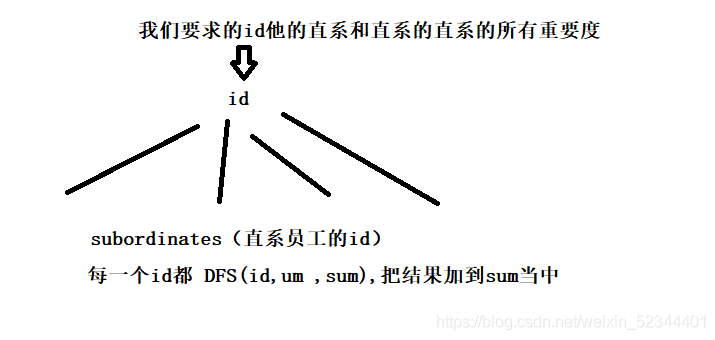
题目的分析,题目给我们的信息就是给到一个id,要求他的直系下属和直系下属的直系下属的importance(重要度),并且vector<Employee*> employees,给我们一个保存员工的数据结构,我们可以先将id和他的重要度绑定起来(哈希表um),这样我们用DFS遍历的时候,就可以先处理当前id,每一个id都要处理他的vector subordinates(这个是他的直系员工的id),再去遍历当前id的直系下属.

for(int id: um[id]->subordinates)
        {
            //对于当前我们需要sum加上加上当前id的重要度
            sum += um[id]->importance;
            //遍历当前id的所有直系下属
            DFS(id,um,sum);
        }

// 题目答案:
class Solution {
public:
    void DFS(int id,unordered_map<int,Employee*>& um,int& sum)
    {
        //对于每一个id，下属的id都会有属于他们的vector<int> subordinates;
        //所以我们都要去遍历当前id的subordinates
        for(int id: um[id]->subordinates)
        {
            //对于当前我们需要sum加上加上当前id的重要度
            sum += um[id]->importance;
            //遍历当前id的直系下属(**一路走到黑**),统计完的结果放到sum当中
            DFS(id,um,sum);
        }
    }

    int getImportance(vector<Employee*> employees, int id) {
        //单个员工 id ，返回这个员工和他所有下属的重要度之和。
        //DFS:深度遍历这个员工的旗下所有重要度之和，这题适合一条路走到黑
        //因为在vector中的查找都是O（N）的时间复杂度，我们选择用哈希表，并且将id与员工的指针建立映射,因为我们在DFS中要使用到用id找到员工
        unordered_map<int,Employee*> um;
        for(Employee* e : employees)
        {
            //将employees的数据导入us（哈希表中）
            um[e->id] = e;
        }
        int sum = um[id]->importance;//提前加上当前id的重要度
        //dfs是遍历当前id的subordinates的重要度
        DFS(id, um,sum);
        return sum;
    }
};

这道题之后实际上后面的题目也都是类似的，大家从这道题开始可以尝试自己写一写，再看看我的代码解析，这样帮助理解！

三、leetcode 图像渲染

733. 图像渲染

这题实际上用bfs,dfs都可以,这里我们讲的是dfs,所以我们用dfs的方式解决,一开始我的想法是,遍历每一个位置的上下左右,将合法的位置并且是旧颜色的改成新颜色.

注：方向矩阵的概念：

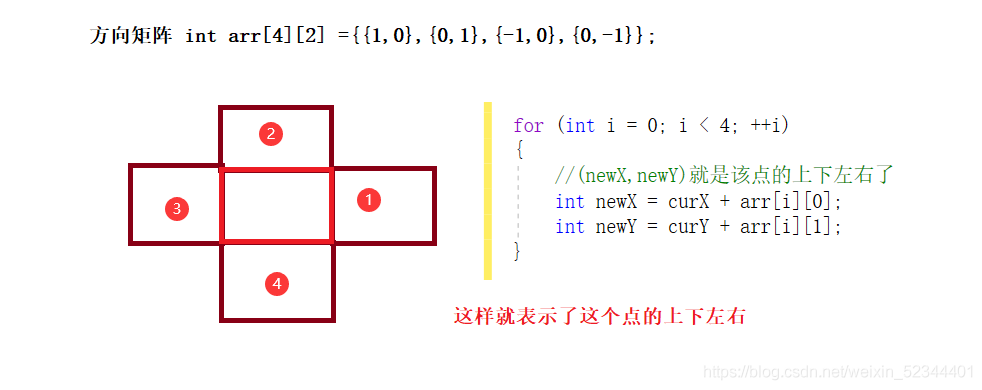
int arr[4][2] ={{1,0},{0,1},{-1,0},{0,-1}};//方向矩阵
    void DFS(vector<vector<int>>& image, int curX, int curY, int newColor,int row ,int col,int oldcolor)
    {
        image[curX][curY] = newColor;//上色
        //遍历 (sr，sc)的上下左右 -- 我们可以设置一个全局的方向矩阵
        for(int i=0;i<4;++i)
        {
            //(newX,newY)就是该点的上下左右了
            int newX = curX+arr[i][0];
            int newY = curY+arr[i][1];
            if(newX<0||newX>=row
            ||newY<0||newY>=col)
            continue;//表示新的坐标越界了不符合要求，跳过

            //走到这里表示新的坐标没有问题,如果是就颜色我们就上色
            if(image[newX][newY] == oldcolor)
            {
                //当前的点处理完，我们处理下一个点
                DFS(image,newX,newY,newColor,row,col,oldcolor);
            }
            else
            continue;
        }
    }

但是这样子会有一个问题,当测试用例为新颜色和旧颜色相同的时候就会变成了死递归,所以我们少不了用标记矩阵,将我们走过的位置标记了他就不会重复走了。

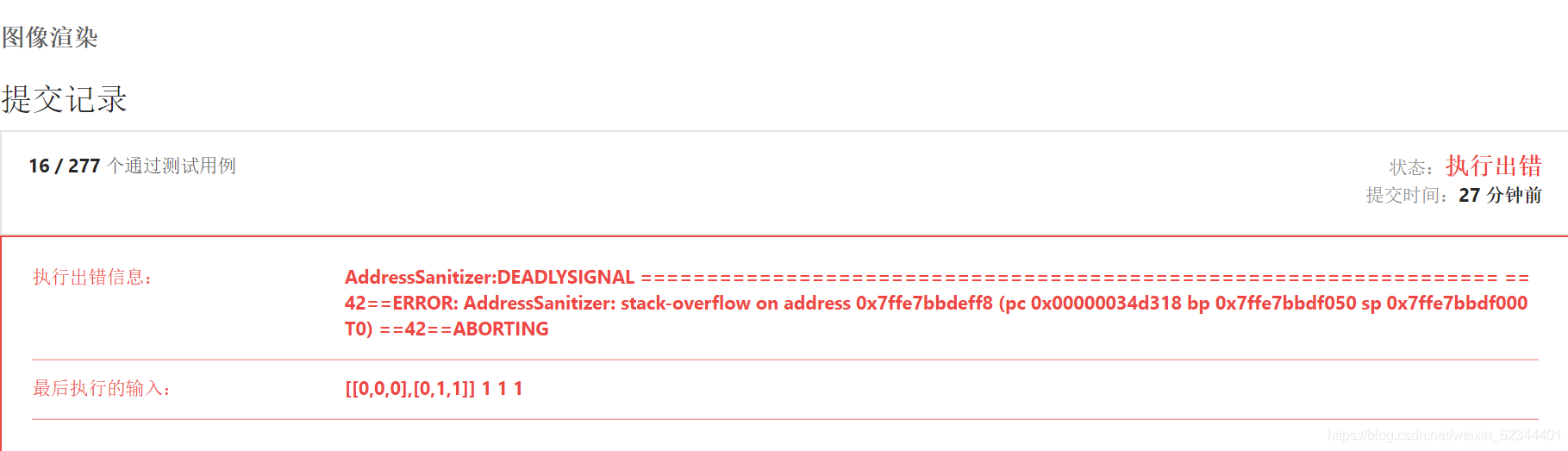
以下为本道题的全部代码

int arr[4][2] ={ { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
class Solution {
public:
    void DFS(vector<vector<int>>& image, int curX, int curY, int newColor,vector<vector<int>>& visited,int row ,int col,int oldColor)
    {
        //给当前位置染色
         image[curX][curY] = newColor;
         //标记当前位置已经使用了
         visited[curX][curY]=1;

        //遍历 (sr，sc)的上右下左 -- 我们可以设置一个全局的方向矩阵
        for(int i=0;i<4;++i)
        {
            //(newX,newY)就是该点的上下左右了
            int newX = curX+arr[i][0];
            int newY = curY+arr[i][1];
            //判断新坐标是否合法
            if(newX<0 || newX>=row
            || newY<0 || newY>=col)
            continue;

            //如果是没有访问过的并且是旧颜色就递归这个点的周围
            if(visited[newX][newY] == 0 &&
               image[newX][newY] == oldColor)
                 DFS(image,newX,newY,newColor,visited,row,col,oldColor) ; 

        }
    }
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
    //我们这道题也可以用BFS，DFS做都没问题，我们这里讲到DFS，所以就用DFS的思路解决
        int row = image.size();
        int col = image[0].size();
        int oldColor =image[sr][sc];
        //初始化标记矩阵，没访问过的置成0
        vector<vector<int>> visited(row,vector<int>(col,0));
        DFS(image,sr,sc,newColor,visited,row,col,oldColor);
        return image;
    }
};

四、leetcode 被围绕的区域

130. 被围绕的区域

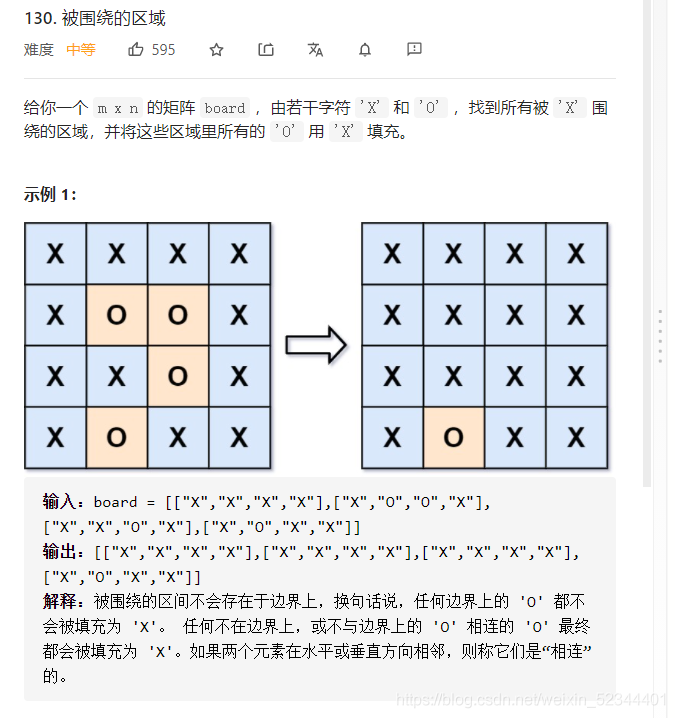
本题就是想将全部没有与外围一圈O联通的O换成X，与外界连通的O不做改变
思路：拿到这样一道题，我们要将与外界O相连的O全部遍历到，所以会用到深度优先搜索，那么我们就可以从矩阵的外围一圈（第一行，最后一行，第一列，最后一列）出发，将外围的每一个O都深度搜索，将搜索到的O（即与外界相连的先换成#）
最后再将O换成#，将#换回O。当然也可以用标记矩阵来写，都是可以的，这里两种方法都写出来看看

1.不使用标记矩阵

int arr[4][2] ={ { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
class Solution {
public:
    void DFS(vector<vector<char>>& board,int row,int col,int curX,int curY)
    {
        //当前点就是联通的‘O'
        board[curX][curY] ='#';
        for(int i =0;i<4;++i)
        {
            int newX = curX+arr[i][0];
            int newY = curY+arr[i][1];
            if(newX<0||newX>=row
            ||newY<0||newY>=col)
            continue;
            if(board[newX][newY]=='O')
            DFS(board,row,col,newX,newY);
        }
    }
    void solve(vector<vector<char>>& board) {
        //我们可以从每一个边界的O出发，链接的O就是不用改的，其他的都是要改成‘X'的
        //但是我们可以通过修改与外面相连的O暂时修改#，就不需要标记矩阵了
        int row =board.size();
        int col=board[0].size();
        for(int i=0;i<row;++i)
        {
            if(board[i][0] =='O')
            DFS(board,row,col,i,0);
            if(board[i][col-1] =='O')
            DFS(board,row,col,i,col-1);
        }
        for(int j =0;j<col;++j)
        {
            if(board[0][j]=='O')
            DFS(board,row,col,0,j);
            if(board[row-1][j]=='O')
            DFS(board,row,col,row-1,j);
        }
        for(int i =0;i<row;++i)
        {
            for(int j =0;j<col;++j)
            {
                if(board[i][j]=='O')
                board[i][j]='X';
                if(board[i][j]=='#')
                board[i][j]='O';
            }
        }
        return ;
    }
};

2.使用标记矩阵

int arr[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
class Solution {
public:
    void DFS(vector<vector<int>>& visited,vector<vector<char>>& board,int row,int col,int curX ,int curY)
    {
        //与外界联通的还是O，我们标记为1
        visited[curX][curY] = 1;

        for(int i =0;i<4;++i)
        {
            int newx = curX+arr[i][0];
            int newy = curY+arr[i][1];
            if(newx<0||newx>=row||
            newy<0||newy>=col)
            continue;
            //没有被访问过的位置（防止重复递归）&& 为O的位置我们才递归
            if(visited[newx][newy]==0&&
            board[newx][newy]=='O')
            {
                DFS(visited,board,row,col,newx,newy);
            }
        }
    }
    void solve(vector<vector<char>>& board) {
        //思路：我们从周围的O出发，与边界O DFS都能获取到的位置我们都可以做个标记
        //最后将标记的不动，没标记的换成'X'(内陆)。
        int row = board.size();
        int col=board[0].size();
        vector<vector<int>> visited(row,vector<int>(col,0));
        //遍历周围为O的位置
        //两列
        for(int i =0;i<row;++i)
        {
            if(board[i][0]=='O')
            DFS(visited,board,row,col,i,0);
            if(board[i][col-1]=='O')
            DFS(visited,board,row,col,i,col-1);
        }
        //两行
        for(int j =0;j<col;++j)
        {
            if(board[0][j]=='O')
            DFS(visited,board,row,col,0,j);
            if(board[row-1][j]=='O')
            DFS(visited,board,row,col,row-1,j);
        }
        //最后将没有标记的O换成X，标记了的不变
        for(int i =0;i<row;++i)
        {
            for(int j =0;j<col;++j)
            {
                if(visited[i][j]==0)
                board[i][j] = 'X';
                cout<<visited[i][j];
            }
        }
    }
};

五、岛屿数量

200. 岛屿数量

有了前面题的基础，对于这道题可谓是信手拈来，详情请看注释：

int arr[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
class Solution {
public:
    void DFS(vector<vector<int>>& visited,vector<vector<char>>& grid,int row,int col,int curx,int cury)
    {
        //将当前位置标记为走过
        visited[curx][cury]=1;
        for(int i =0;i<4;++i)
        {
            int newx = curx+arr[i][0];
            int newy = cury+arr[i][1];
            if(newx<0||newx>=row||newy<0||newy>=col)
                continue;
            if(grid[newx][newy]=='1'&&visited[newx][newy]==0)
            DFS(visited,grid,row,col,newx,newy);
        }
    }
    int numIslands(vector<vector<char>>& grid) {
        //这道题其实也是用BFS，DFS都可以解，用DFS的话我的思路是从第一个开始遍历，遇到一个visited没有访问过的1就去遍历他的上下左右，将他周围的1都遍历，在将次数加一
        int row =grid.size();
        int col=grid[0].size();
        int count =0;
        vector<vector<int>> visited(row,vector<int>(col,0));
        for(int i =0;i<row;++i)
        {
            for(int j =0;j<col;++j)
            {
                if(visited[i][j]==0&&grid[i][j]=='1')
                {
                    DFS(visited,grid,row,col,i,j);
                    count++;
                }
            }
        }
        return count;
    }
};

六、 小练习：岛屿的最大面积

695. 岛屿的最大面积

这道题留给大家作为一个小练习，有了前面的基础，相信这道题想必不是问题！！

总结

回溯思想DFS一些难度较大的题一起讲！！DFS的学习时要注意多调试，想清楚了再下手写，这样往往能够事半功倍

到此这篇关于最短时间学会基于C++实现DFS深度优先搜索的文章就介绍到这了,更多相关C++ DFS深度优先搜索内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！