C++的最短路径的弗洛伊德算法案例讲解

现在我们有这么一张图：

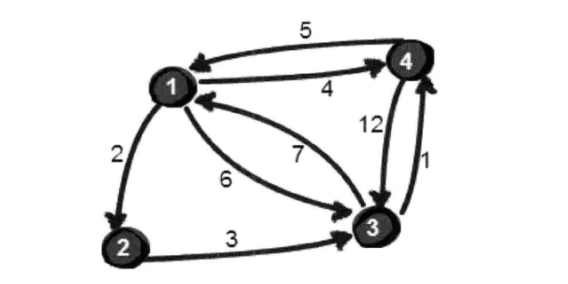
我们要做的是求出从某一点到达任意一点的最短距离，我们先用邻接矩阵来建图，map[i][j]表示从i点到j点的距离，把自己到自己设为0，把自己到不了的边初始化为无穷大，代码为：

//初始化
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=inf;
    //读入边
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d%d",&t1,&t2,&t3);
        map[t1][t2]=t3;
    }

最后，建好的图可以用表格来表示：

现在，我们来思考，假设我们来找一个中转的点，看他们的路程会不会改变，我们先以1号顶点作为中转点最为例子，制图：

我们发现，图有了变化，我们怎么判断以1号顶点作为中转点图的路程是不是更短呢，我们只需要判断map[i][1]+map[1][j]的路程是不是比map[i][j]的路程更短，就可以判断，

代码为：

for(int i=1; i<=n; i++)
    for(int j=1; j<=n; j++)
        if(map[i][1]+map[1][j]<map[i][j])
            map[i][j]=map[i][1]+map[1][j];

现在该怎么办呢，我们接着以2号顶点作为中转点，很简单代码修改一句就就可以：

for(int i=1; i<=n; i++)
    for(int j=1; j<=n; j++)
        if(map[i][2]+map[2][j]<map[i][j])
            map[i][j]=map[i][2]+map[2][j];

现在我们是不是发现了一个规律，只要不断的遍历每一个点，并且以每一个点作为中转点看看它的值会不会改变，就可以得到从一个点到任意一个点的最短路径，也就是多源最短路，这就是弗洛伊德算法，代码为：

for(int k=1; k<=n; k++)
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(map[i][k]+map[k][j]<map[i][j])
                map[i][j]=map[i][k]+map[k][j];

这样就可以遍历每个顶点，找出所有的最短路，算法的复杂度为O(n^3).

对于我一开始提出的问题，完整的代码为：

#include <stdio.h>
#include <string.h>
#include <string>
#include <iostream>
#include <stack>
#include <queue>
#include <vector>
#include <algorithm>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int inf=1<<29;
int main()
{
    int map[10][10],n,m,t1,t2,t3;
    scanf("%d%d",&n,&m);//n表示顶点个数，m表示边的条数
    //初始化
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            if(i==j)
                map[i][j]=0;
            else
                map[i][j]=inf;
    //读入边
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d%d",&t1,&t2,&t3);
        map[t1][t2]=t3;
    }
    //弗洛伊德(Floyd)核心语句
    for(int k=1; k<=n; k++)
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                if(map[i][k]+map[k][j]<map[i][j])
                    map[i][j]=map[i][k]+map[k][j];
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=n; j++)
            printf("%10d",map[i][j]);
        printf("\n");
    }
    return 0;
}

给出样例：

输入：

4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12

输出：

         0         2         5         4
         9         0         3         4
         6         8         0         1
         5         7        10         0

输出的就是我建图的时候用的表格，可以表示任意一点到任意一点的最短距离。
如果有什么不对的地方，欢迎指正~~

到此这篇关于C++的最短路径的弗洛伊德算法案例讲解的文章就介绍到这了,更多相关C++的最短路径的弗洛伊德算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • c++查询最短路径示例

    c++查询最短路径示例

    复制代码 代码如下: //shortest_path.c#include<stdio.h>#include<stdlib.h>//用file#include<string.h>//可用gets(),puts()#include"shortest_path.h"#define MAX 32767#define MENU "欢迎进入导航系统!\n==========菜单===========\n0.载入北外地图\n1.建立地图\n2.查询最短路

  • C++用Dijkstra(迪杰斯特拉)算法求最短路径

    C++用Dijkstra(迪杰斯特拉)算法求最短路径

    算法介绍 迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法.是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题.迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止.Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低. 算法思想 按路径长度递增次序产生算法: 把顶点集合V分成两组: (1)S:已求出的顶点的集合(初始时只含有源点V0) (2)V-S=T:尚未确定的顶点集合 将T中顶点按递增

  • Dijkstra算法最短路径的C++实现与输出路径

    Dijkstra算法最短路径的C++实现与输出路径

    某个源点到其余各顶点的最短路径 这个算法最开始心里怕怕的,不知道为什么,花了好长时间弄懂了,也写了一遍,又遇到时还是出错了,今天再次写它,心里没那么怕了,耐心研究,懂了之后会好开心的,哈哈 Dijkstra算法: 图G 如图:若要求从顶点1到其余各顶点的最短路径,该咋求: 迪杰斯特拉提出"按最短路径长度递增的次序"产生最短路径. 首先,在所有的这些最短路径中,长度最短的这条路径必定只有一条弧,且它的权值是从源点出发的所有弧上权的最小值,例如:在图G中,从源点1出发有3条弧,其中以弧(1

  • C++实现多源最短路径之Floyd算法示例

    本文实例讲述了C++实现多源最短路径之Floyd算法.分享给大家供大家参考,具体如下: #include<cstdio> #include<cstring> #include<iostream> #define MAX 999 using namespace std; int n,m; int e[MAX][MAX]; void Init() { for(int i=1; i<=n; ++i) for(int j=1; j<=n; ++j) { if(i==

  • C++求所有顶点之间的最短路径（用Dijkstra算法）

    本文实例为大家分享了C++求所有顶点之间最短路径的具体代码,供大家参考,具体内容如下 一.思路: 不能出现负权值的边 (1)轮流以每一个顶点为源点,重复执行Dijkstra算法n次,就可以求得每一对顶点之间的最短路径及最短路径长度,总的执行时间为O(n的3次方) (2)另一种方法:用Floyd算法,总的执行时间为O(n的3次方)(另一文章会写) 二.实现程序: 1.Graph.h:有向图 #ifndef Graph_h #define Graph_h #include <iostream> u

  • C++所有顶点之间的最短路径

    本文实例为大家分享了C++所有顶点之间最短路径的具体代码,供大家参考,具体内容如下 一.思路: 不能出现负权值的边 用Floyd算法,总的执行时间为O(n的3次方) k从顶点0一直到顶点n-1, 如果,有顶点i到顶点j之间绕过k,使得两顶点间的路径更短,即dist[i][k] + dist[k][j] < dist[i][j],则修改:dist[i][j] 如:(1)当k=0时, 顶点2绕过顶点0到达顶点1,使得路径为:3+1 < dist[2][1],所以,要修改dist[2][1]=4,同

  • C++计算任意权值的单源最短路径（Bellman-Ford）

    本文实例为大家分享了C++计算任意权值单源最短路径的具体代码,供大家参考,具体内容如下 一.有Dijkstra算法求最短路径了,为什么还要用Bellman-Ford算法 Dijkstra算法不适合用于带有负权值的有向图. 如下图: 用Dijkstra算法求顶点0到各个顶点的最短路径: (1)首先,把顶点0添加到已访问顶点集合S中,选取权值最小的邻边<0, 2>,权值为5 记录顶点2的最短路径为:dist[2]=5, path[2]=0,把顶点2添加到集合S中. 顶点2,没有邻边(从顶点2出发,

  • C++的最短路径的弗洛伊德算法案例讲解

    C++的最短路径的弗洛伊德算法案例讲解

    现在我们有这么一张图: 我们要做的是求出从某一点到达任意一点的最短距离,我们先用邻接矩阵来建图,map[i][j]表示从i点到j点的距离,把自己到自己设为0,把自己到不了的边初始化为无穷大,代码为: //初始化 for(int i=1; i<=n; i++) for(int j=1; j<=n; j++) if(i==j) map[i][j]=0; else map[i][j]=inf; //读入边 for(int i=1; i<=m; i++) { scanf("%d%d%d

  • Java之理解Redis回收算法LRU案例讲解

    如何通俗易懂的理解LRU算法? 1.LRU是什么? LRU全称Least Recently Used,也就是最近最少使用的意思,是一种内存管理算法,最早应用于Linux操作系统. LRU算法基于一种假设:长期不被使用的数据,在未来被用到的几率也不大.因此,当数据所占内存达到一定阈值时,我们要移除掉最近最少被使用的数据. LRU算法应用:可以在内存不够时,从哈希表移除一部分很少访问的用户. LRU是什么?按照英文的直接原义就是Least Recently Used,最近最久未使用法,它是按照一个非

  • SPFA 算法实例讲解

    SPFA 算法实例讲解

    适用范围:给定的图存在负权边,这时类似Dijkstra等算法便没有了用武之地,而Bellman-Ford算法的复杂度又过高,SPFA算法便 派上用场了. 我们约定有向加权图G不存在负权回路,即最短路径一定存在.当然,我们可以在执行该算法前做一次拓扑排序,以判断是否存在负权回路,但这不是我们讨论的重 点. 算法思想:我们用数组d记录每个结点的最短路径估计值,用邻接表来存储图G.我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的 结点,优化时每次取出队首结点u,并且用u点当前的最短路

  • NetworkX之Prim算法(实例讲解)

    NetworkX之Prim算法(实例讲解)

    引言 Prim算法与Dijkstra的最短路径算法类似,它采用贪心策略.算法开始先把图中权值最小的边添加到树T中,然后不断把权值最小的边E(E的一个端点在T中,另一个在G-T中).当没有符合条件的E时算法结束,此时T就是G的一个最小生成树. NetworkX是一款Python的软件包,用于创造.操作复杂网络,以及学习复杂网络的结构.动力学及其功能. 本文借助networkx.Graph类实现Prim算法. 正文 Prim算法的代码 Prim def prim(G, s): dist = {} #

  • 基于Python实现迪杰斯特拉和弗洛伊德算法

    图搜索之基于Python的迪杰斯特拉算法和弗洛伊德算法,供大家参考,具体内容如下 Djstela算法 #encoding=UTF-8 MAX=9 ''' Created on 2016年9月28日 @author: sx ''' b=999 G=[[0,1,5,b,b,b,b,b,b],\ [1,0,3,7,5,b,b,b,b],\ [5,3,0,b,1,7,b,b,b],\ [b,7,b,0,2,b,3,b,b],\ [b,5,1,2,0,3,6,9,b],\ [b,b,7,b,3,0,b,5

  • Java之哈夫曼压缩原理案例讲解

    Java之哈夫曼压缩原理案例讲解

    1. 哈夫曼压缩原理 首先要明确一点,计算机里面所有的文件都是以二进制的方式存储的. 在计算机的存储单元中,一个ASCII码值占一个字节,1个字节等于8位(1Byte = 8bit) 可以参考这个网站: ASCII码在线转换计算器 以"JavaJavaJavaJavaJavaJava"这个字符串为例,它在计算机内部是这样存储的(每一个字符的ASCII码转换为二进制存储起来): public static void main(String[] args) { String beforeS

  • python实现CTC以及案例讲解

    python实现CTC以及案例讲解

    在大多数语音识别任务中,我们都缺少文本和音频特征的alignment,Connectionist Temporal Classification作为一个损失函数,用于在序列数据上进行监督式学习,可以不需要对齐输入数据及标签. 对于输入序列 X = [ x 1 , x 2 , . . , x T ] X=[x_1, x_2, .., x_T] X=[x1​,x2​,..,xT​] 和 输出序列 Y = [ y 1 , y 2 , . . . , y U ] Y = [y_1, y_2, ...,

  • Java快速排序案例讲解

    Java快速排序案例讲解

    交换类排序主要是通过两两比较待排元素的关键字,若发现与排序要求相逆,则"交换"之.在这类排序方法中最常见的是冒泡排序和快速排序.上一篇简单写了冒泡排序,这次简单写一写快速排序. 快速排序的思想: 快速排序是将分治法运用到排序问题中的一个典型例子,其基本思想是:通过一个枢轴(pivot)元素将 n 个元素的序列分为左.右两个子序列 Ll 和 Lr,其中子序列 Ll中的元素均比枢轴元素小,而子序列 Lr 中的元素均比枢轴元素大,然后对左.右子序列分别进行快速排序,在将左.右子序列排好序后,

  • Java之api网关断言及过滤器案例讲解

    Java之api网关断言及过滤器案例讲解

    目录 一.什么是api网关? 二.常见的api网关 三.使用步骤 1.Spring Cloud Gateway 2.优缺点 3.传统的过滤器 4.使用gateway 4.1module 4.2添加pom依赖 4.3yaml配置 4.4主程序开启注解@EnableDiscoveryClient 四.执行流程 五.断言 5.1: 自定义断言 5.2: 过滤器 一.什么是api网关? 所谓的API网关,就是指后台系统的统一入口,它封装了应用程序的内部结构,为客户端提供统一 路由服务,一些与业务本身功能

  • C语言深入探究直接插入排序与希尔排序使用案例讲解

    C语言深入探究直接插入排序与希尔排序使用案例讲解

    目录 一.直接插入排序 1.1直接插入排序引入 1.2直接插入排序的核心思想与算法分析 1.3实例说明 1.4直接插入排序代码实现 1.5直接插入排序性能分析 二.希尔排序 2.1希尔排序引入 2.2希尔排序的核心思想与算法分析 2.3实例说明 2.4希尔排序代码实现 2.5希尔排序性能分析 一.直接插入排序 1.1直接插入排序引入 排序是我们生活中经常会面对的问题,以打扑克牌为例,你摸的手牌肯定是杂乱的,你一定会将小牌移动到大牌的左面,大牌移动到小牌的右面,这样顺序就算理好了.这里我们的理牌方

随机推荐