C++二叉树的直径与合并详解

目录

• 二叉树的直径
• 给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
• 思路
• 合并二叉树
• 给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。
• 思路
• 1.确定递归函数的参数和返回值：
• 2.确定终止条件：
• 3.确定单层递归的逻辑：
• 总结

二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :

给定二叉树

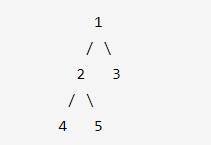
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

思路

求左右孩子深度的和的最大值

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res=0; //定义一个全局变量
    int depth(TreeNode* root){  //求深度
        if(root==nullptr)  return 0;
        int L=depth(root->left);
        int R=depth(root->right);
        res=max(res,L+R);
        return max(L,R)+1;
    }
    int diameterOfBinaryTree(TreeNode* root) {
        depth(root);
        return res;
    }
};

合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

思路

1.确定递归函数的参数和返回值：

首先那么要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。

代码如下：

TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2)

2.确定终止条件：

因为是传入了两个树，那么就有两个树遍历的节点t1 和 t2，如果t1 == NULL 了，两个树合并就应该是 t2 了啊（如果t2也为NULL也无所谓，合并之后就是NULL）。

反过来如果t2 == NULL，那么两个数合并就是t1（如果t1也为NULL也无所谓，合并之后就是NULL）。

代码如下：

if (t1 == NULL) return t2; // 如果t1为空，合并之后就应该是t2
if (t2 == NULL) return t1; // 如果t2为空，合并之后就应该是t1

3.确定单层递归的逻辑：

单层递归的逻辑就比较好些了，这里我们用重复利用一下t1这个树，t1就是合并之后树的根节点（就是修改了原来树的结构）。
那么单层递归中，就要把两棵树的元素加到一起。

t1->val += t2->val;

接下来t1 的左子树是：合并 t1左子树 t2左子树之后的左子树。

t1 的右子树：是 合并 t1右子树 t2右子树之后的右子树。

最终t1就是合并之后的根节点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        // 判空
        if(root1==nullptr) return root2;
        if(root2==nullptr) return root1;
        // 修改了t1的数值和结构
        root1->val+=root2->val;
        root1->left=mergeTrees(root1->left,root2->left);
        root1->right=mergeTrees(root1->right,root2->right);
        return root1;
    }
};

总结

本篇文章就到这里了，希望能给你带来帮助，也希望您能够多多关注我们的更多内容!