带你了解Java数据结构和算法之2-3-4树

目录

• 1、2-3-4 树介绍
• 2、搜索2-3-4树
• 3、插入
• 1、节点分裂
• 2、根的分裂
• 4、完整源码实现
• 5、2-3-4树和红黑树　　
• ①、对应规则
• ②、操作等价
• 6、2-3-4 树的效率
• 总结

1、2-3-4 树介绍

2-3-4树每个节点最多有四个字节点和三个数据项，名字中 2,3,4 的数字含义是指一个节点可能含有的子节点的个数。对于非叶节点有三种可能的情况：

①、有一个数据项的节点总是有两个子节点；

②、有二个数据项的节点总是有三个子节点；

③、有三个数据项的节点总是有四个子节点；

简而言之，非叶节点的子节点数总是比它含有的数据项多1。如果子节点个数为L，数据项个数为D，那么：L = D + 1

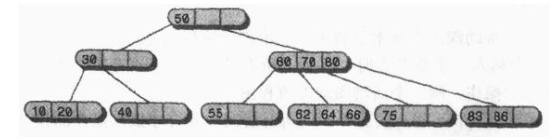
叶节点（上图最下面的一排）是没有子节点的，然而它可能含有一个、两个或三个数据项。空节点是不会存在的。

树结构中很重要的一点就是节点之间关键字值大小的关系。在二叉树中，所有关键字值比某个节点值小的节点都在这个节点左子节点为根的子树上；所有关键字值比某个节点值大的节点都在这个节点右子节点为根的子树上。2-3-4 树规则也是一样，并且还加上以下几点：

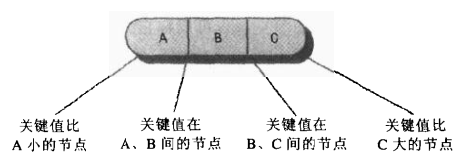
为了方便描述，用从0到2的数字给数据项编号，用0到3的数字给子节点编号，如下图：

①、根是child0的子树的所有子节点的关键字值小于key0；

②、根是child1的子树的所有子节点的关键字值大于key0并且小于key1；

③、根是child2的子树的所有子节点的关键字值大于key1并且小于key2；

④、根是child3的子树的所有子节点的关键字值大于key2。

简化关系如下图，由于2-3-4树中一般不允许出现重复关键值，所以不用考虑比较关键值相同的情况。

2、搜索2-3-4树

查找特定关键字值的数据项和在二叉树中的搜索类似。从根节点开始搜索，除非查找的关键字值就是根，否则选择关键字值所在的合适范围，转向那个方向，直到找到为止。

比如对于下面这幅图，我们需要查找关键字值为 64 的数据项。

首先从根节点开始，根节点只有一个数据项50，没有找到，而且因为64比50大，那么转到根节点的子节点child1。60|70|80 也没有找到，而且60<64<70，所以我们还是找该节点的child1,62|64|66，我们发现其第二个数据项正好是64，于是找到了。

3、插入

新的数据项一般要插在叶节点里，在树的最底层。如果你插入到有子节点的节点里，那么子节点的编号就要发生变化来维持树的结构，因为在2-3-4树中节点的子节点要比数据项多1。

插入操作有时比较简单，有时却很复杂。

①、当插入没有满数据项的节点时是很简单的，找到合适的位置，只需要把新数据项插入就可以了，插入可能会涉及到在一个节点中移动一个或其他两个数据项，这样在新的数据项插入后关键字值仍保持正确的顺序。如下图：

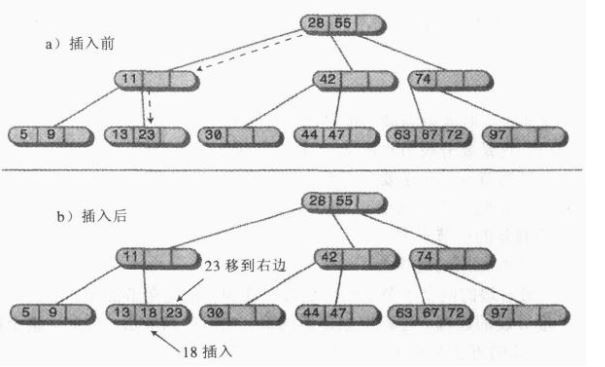
②、如果往下寻找插入位置的途中，节点已经满了，那么插入就变得复杂了。发生这种情况时，节点必须分裂，分裂能保证2-3-4树的平衡。

ps：这里讨论的是自顶向下的2-3-4树，因为是在向下找到插入点的路途中节点发生了分裂。把要分裂的数据项设为A,B,C，下面是节点分裂的情况（假设分裂的节点不是根节点）：

1、节点分裂

一、创建一个新的空节点，它是要分裂节点的兄弟，在要分裂节点的右边；

二、数据项C移到新节点中；

三、数据项B移到要分裂节点的父节点中；

四、数据项A保留在原来的位置；

五、最右边的两个子节点从要分裂处断开，连到新节点上。

上图描述了节点分裂的例子，另一种描述节点分裂的说法是4-节点变成了两个 2- 节点。节点分裂是把数据向上和向右移动，从而保持了数的平衡。一般插入只需要分裂一个节点，除非插入路径上存在不止一个满节点时，这种情况就需要多重分裂。

2、根的分裂

如果一开始查找插入节点时就碰到满的根节点，那么插入过程更复杂：

①、创建新的根节点，它是要分裂节点的父节点。

②、创建第二个新的节点，它是要分裂节点的兄弟节点；

③、数据项C移到新的兄弟节点中；

④、数据项B移到新的根节点中；

⑤、数据项A保留在原来的位置；

⑥、要分裂节点最右边的两个子节点断开连接，连到新的兄弟节点中。

上图便是根分裂的情况，分裂完成之后，整个树的高度加1。另外一种描述根分裂的方法是说4-节点变成三个2-节点。

注意：插入时，碰到没有满的节点时，要继续向下寻找其子节点进行插入。如果直接插入该节点，那么还要进行子节点的增加，因为在2-3-4树中节点的子节点个数要比数据项多1；如果插入的节点满了，那么就要进行节点分裂。下图是一系列插入过程，有4个节点分裂了，两个是根，两个是叶节点：

4、完整源码实现

分为节点类Node,表示每个节点的数据项类DataItem,以及最后的2-3-4树类Tree234.class

package com.ys.tree.twothreefour;
public class Tree234 {
    private Node root = new Node() ;
    /*public Tree234(){
        root = new Node();
    }*/
    //查找关键字值
    public int find(long key){
        Node curNode = root;
        int childNumber ;
        while(true){
            if((childNumber = curNode.findItem(key))!=-1){
                return childNumber;
            }else if(curNode.isLeaf()){//节点是叶节点
                return -1;
            }else{
                curNode = getNextChild(curNode,key);
            }
        }
    }
    public Node getNextChild(Node theNode,long theValue){
        int j;
        int numItems = theNode.getNumItems();
        for(j = 0 ; j < numItems ; j++){
            if(theValue < theNode.getItem(j).dData){
                return theNode.getChild(j);
            }
        }
        return theNode.getChild(j);
    }
    //插入数据项
    public void insert(long dValue){
        Node curNode = root;
        DataItem tempItem = new DataItem(dValue);
        while(true){
            if(curNode.isFull()){//如果节点满数据项了，则分裂节点
                split(curNode);
                curNode = curNode.getParent();
                curNode = getNextChild(curNode, dValue);
            }else if(curNode.isLeaf()){//当前节点是叶节点
                break;
            }else{
                curNode = getNextChild(curNode, dValue);
            }
        }//end while
        curNode.insertItem(tempItem);
    }
    public void split(Node thisNode){
        DataItem itemB,itemC;
        Node parent,child2,child3;
        int itemIndex;
        itemC = thisNode.removeItem();
        itemB = thisNode.removeItem();
        child2 = thisNode.disconnectChild(2);
        child3 = thisNode.disconnectChild(3);
        Node newRight = new Node();
        if(thisNode == root){//如果当前节点是根节点，执行根分裂
            root = new Node();
            parent = root;
            root.connectChild(0, thisNode);
        }else{
            parent = thisNode.getParent();
        }
        //处理父节点
        itemIndex = parent.insertItem(itemB);
        int n = parent.getNumItems();
        for(int j = n-1; j > itemIndex ; j--){
            Node temp = parent.disconnectChild(j);
            parent.connectChild(j+1, temp);
        }
        parent.connectChild(itemIndex+1, newRight);
        //处理新建的右节点
        newRight.insertItem(itemC);
        newRight.connectChild(0, child2);
        newRight.connectChild(1, child3);
    }
    //打印树节点
    public void displayTree(){
        recDisplayTree(root,0,0);
    }
    private void recDisplayTree(Node thisNode,int level,int childNumber){
        System.out.println("levle="+level+" child="+childNumber+" ");
        thisNode.displayNode();
        int numItems = thisNode.getNumItems();
        for(int j = 0; j < numItems+1 ; j++){
            Node nextNode = thisNode.getChild(j);
            if(nextNode != null){
                recDisplayTree(nextNode, level+1, j);
            }else{
                return;
            }
        }
    }
    //数据项
    class DataItem{
        public long dData;
        public DataItem(long dData){
            this.dData = dData;
        }
        public void displayItem(){
            System.out.println("/"+dData);
        }
    }
    //节点
    class Node{
        private static final int ORDER = 4;
        private int numItems;//表示该节点有多少个数据项
        private Node parent;//父节点
        private Node childArray[] = new Node[ORDER];//存储子节点的数组，最多有4个子节点
        private DataItem itemArray[] = new DataItem[ORDER-1];//存放数据项的数组，一个节点最多有三个数据项
        //连接子节点
        public void connectChild(int childNum,Node child){
            childArray[childNum] = child;
            if(child != null){
                child.parent = this;
            }
        }
        //断开与子节点的连接，并返回该子节点
        public Node disconnectChild(int childNum){
            Node tempNode = childArray[childNum];
            childArray[childNum] = null;
            return tempNode;
        }
        //得到节点的某个子节点
        public Node getChild(int childNum){
            return childArray[childNum];
        }
        //得到父节点
        public Node getParent(){
            return parent;
        }
        //判断是否是叶节点
        public boolean isLeaf(){
            return (childArray[0] == null)?true:false;
        }
        //得到节点数据项的个数
        public int getNumItems(){
            return numItems;
        }
        //得到节点的某个数据项
        public DataItem getItem(int index){
            return itemArray[index];
        }
        //判断节点的数据项是否满了（最多3个）
        public boolean isFull(){
            return (numItems == ORDER-1) ? true:false;
        }
        //找到数据项在节点中的位置
        public int findItem(long key){
            for(int j = 0 ; j < ORDER-1 ; j++){
                if(itemArray[j]==null){
                    break;
                }else if(itemArray[j].dData == key){
                    return j;
                }
            }
            return -1;
        }
        //将数据项插入到节点
        public int insertItem(DataItem newItem){
            numItems++;
            long newKey = newItem.dData;
            for(int j = ORDER-2 ; j >= 0 ; j--){
                if(itemArray[j] == null){//如果为空，继续向前循环
                    continue;
                }else{
                    long itsKey = itemArray[j].dData;//保存节点某个位置的数据项
                    if(newKey < itsKey){//如果比新插入的数据项大
                        itemArray[j+1] = itemArray[j];//将大数据项向后移动一位
                    }else{
                        itemArray[j+1] = newItem;//如果比新插入的数据项小，则直接插入
                        return j+1;
                    }
                }
            }
            //如果都为空，或者都比待插入的数据项大，则将待插入的数据项放在节点第一个位置
            itemArray[0] = newItem;
            return 0;
        }
        //移除节点的数据项
        public DataItem removeItem(){
            DataItem temp = itemArray[numItems-1];
            itemArray[numItems-1] = null;
            numItems--;
            return temp;
        }
        //打印节点的所有数据项
        public void displayNode(){
            for(int j = 0 ; j < numItems ; j++){
                itemArray[j].displayItem();
            }
            System.out.println("/");
        }
    }
}

5、2-3-4树和红黑树　　

2-3-4树是多叉树，而红黑树是二叉树，看上去可能完全不同，但是，在某种意义上它们又是完全相同的，一个可以通过应用一些简单的规则变成另一个，而且使他们保持平衡的操作也是一样，数学上称他们为同构。

①、对应规则

应用如下三条规则可以将2-3-4树转化为红黑树：

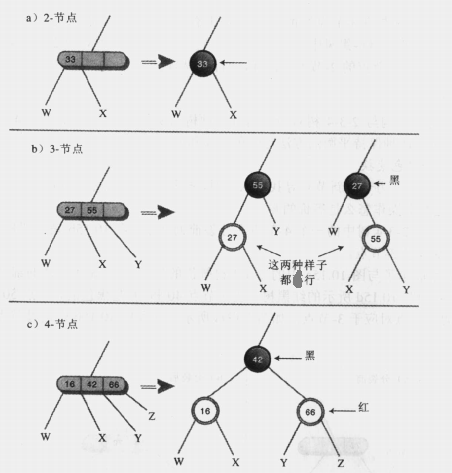
一、把2-3-4树中的每个2-节点转化为红-黑树的黑色节点。

二、把每个3-节点转化为一个子节点和一个父节点，子节点有两个自己的子节点：W和X或X和Y。父节点有另一个子节点：Y或W。哪个节点变成子节点或父节点都无所谓。子节点涂成红色，父节点涂成黑色。

三、把每个4-节点转化为一个父节点和两个子节点。第一个子节点有它自己的子节点W和X；第二个子节点拥有子节点Y和Z。和前面一样，子节点涂成红色，父节点涂成黑色。

下图是一颗2-3-4树转化成对应的红-黑树。虚线环绕的子树是由3-节点和4-节点变成的。转化后符合红-黑树的规则，根节点为红色，两个红色节点不会相连，每条从根到叶节点的路径上的黑节点个数是一样的。　　

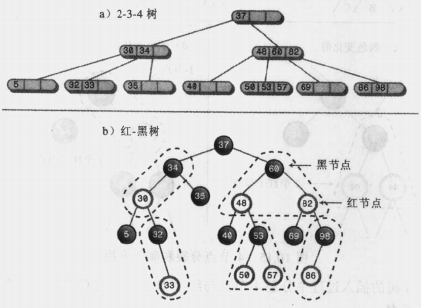
②、操作等价

不仅红-黑树的结构与2-3-4树对应，而且两种树操作也一样。2-3-4树用节点分裂保持平衡，红-黑树用颜色变换和旋转保持平衡。

上图是4-节点分裂。虚线环绕的部分等价于4-节点。颜色变换之后，40,60节点都为黑色的，50节点是红色的。因此，节点 50 和它的父节点70 对于3-节点，如上图虚线所示。

6、2-3-4 树的效率

分析2-3-4树我们可以和红黑树作比较分析。红-黑树的层数（平衡二叉树）大约是log2(N+1)，而2-3-4树每个节点可以最多有4个数据项，如果节点都是满的，那么高度和log4N。因此在所有节点都满的情况下，2-3-4树的高度大致是红-黑树的一半。不过他们不可能都是满的，所以2-3-4树的高度大致在log2(N+1)和log2(N+1)/2。减少2-3-4树的高度可以使它的查找时间比红-黑树的短一些。

但是另一方面，每个节点要查看的数据项就多了，这会增加查找时间。因为节点中用线性搜索来查看数据项，使得查找时间的倍数和M成正比，即每个节点数据项的平均数量。总的查找时间和M*log4N成正比。

总结

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容!