C++栈实现逆波兰式的应用

目录

• 一.定义
• 二.逆波兰式的意义
• 三.逆波兰式的实现
• 1.方法
• 2.代码实现

一.定义

逆波兰式，又称后缀表达式，指的是操作符在其所控制的操作数后面的表达式。
举个例子，1 + 2 * 3 - 4这个表达式是我们熟悉的中缀表达式，那么其所对应的后缀表达式为：1 2 3 * + 4 -。
再来个复杂的例子：1 * (2 + 3) / 5 - 4 / 2其对应的后缀表达式为：1 2 3 + * 5 / 4 2 / -（其中括号由于只是提升表达式优先级的作用，因此不放入后缀表达式中）。

二.逆波兰式的意义

为什么要将看似简单的中缀表达式转换为复杂的逆波兰式，原因就在于这个简单是相对我们人类的思维结构来说的，对计算机而言中序表达式是非常复杂的结构。相对的，逆波兰式在计算机看来却是比较简单易懂的结构。因为计算机普遍采用的内存结构是栈式结构，它执行先进后出的顺序。

三.逆波兰式的实现

1.方法

（1）中缀表达式转化为后缀表达式

对于给出的中缀表达式，如何将其转化为后缀表达式呢？
第一，若遇到操作数则直接输出/存储。
第二，遇到操作符，若此时栈为空或者操作符优先级高于栈顶，则入栈。
第三，若操作符的优先级低于或者等于栈顶，则出栈直至栈空或者优先级低于该操作符。
第四，遇到'(',其后的所有操作符（直至遇到')'）按上述操作入栈或出栈；当遇到')‘时，将'('顶上的所有操作符出栈。

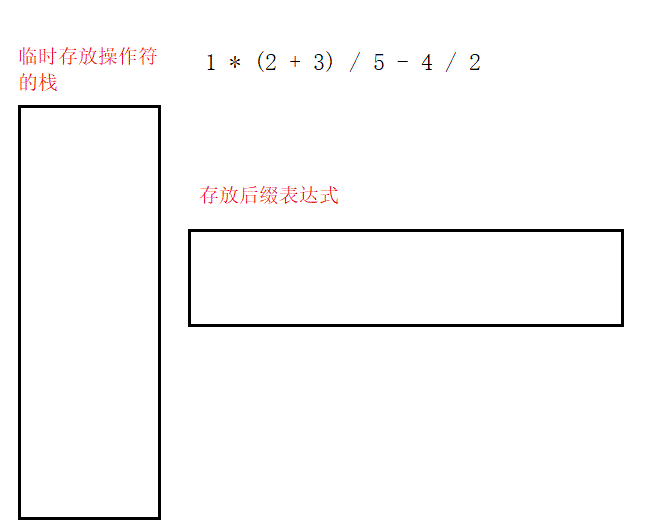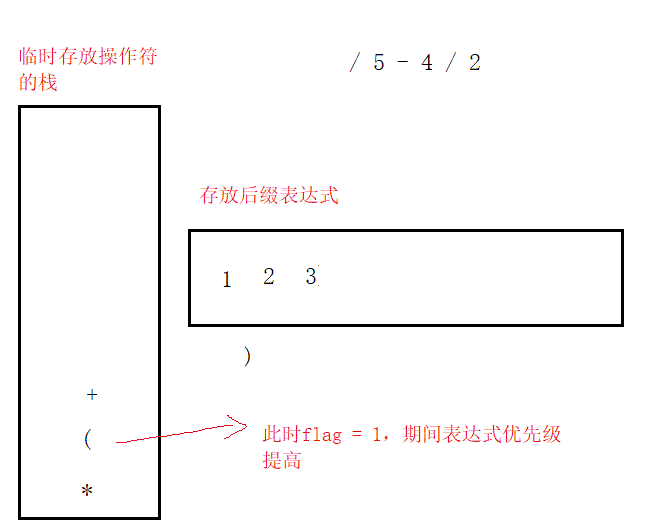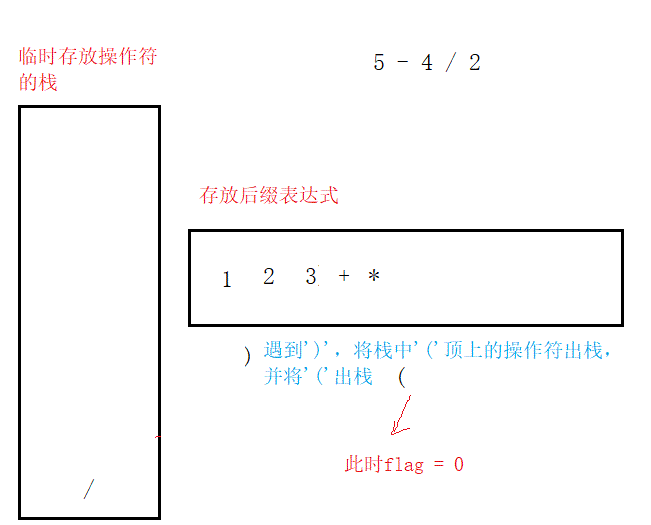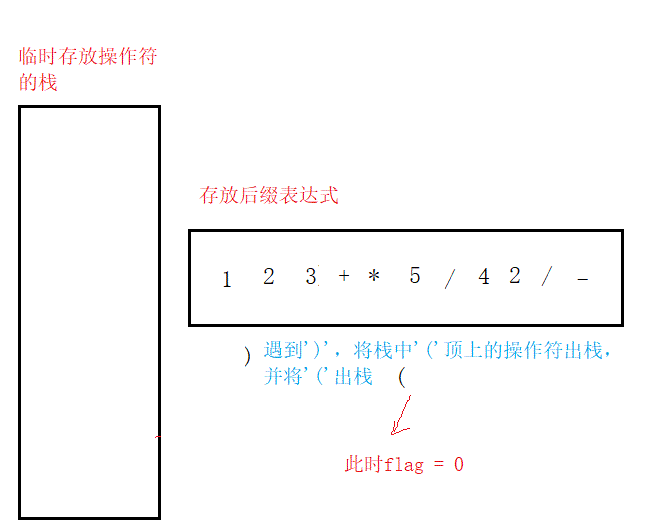
（2）由后缀表达式计算结果

第一，遇到操作数则入栈。
第二，遇到操作符则将栈顶的两个操作数出栈，其中第一个数为右操作数，第二个数为左操作数。
第三，计算结果并将计算的结果入栈。
第四，最后栈顶的结果即为所计算的结果。

2.代码实现

#include <iostream>
#include <string>
#include <stack>
#include <vector>
using namespace std;

string trans(string& s)
{
	string operand;
	stack<char> Operator;
	int flag = 0;//记录括号优先级
	for (const auto& e : s)
	{
		if (e == '(')
		{
			Operator.push(e);
			flag = 1;
			continue;
		}
		if (e == ')')
		{
			flag = 0;
			while (Operator.top() != '(')
			{
				operand.push_back(Operator.top());
				Operator.pop();
			}
			Operator.pop();
			continue;
		}
		//操作符
		if (e == '+' || e == '-' || e == '*' || e == '/')
		{
			if (flag == 1)
			{
				if (Operator.top() == '(')
				{
					Operator.push(e);

				}
				else if ((e == '*' || e == '/') && (Operator.top() == '+' || Operator.top() == '-'))
				{
					Operator.push(e);
				}
				else//操作符的优先级低于或等于栈顶操作符则出栈，直至遇到'('
				{
					while (Operator.top() != '(')
					{
						operand.push_back(Operator.top());
						Operator.pop();
					}
					Operator.push(e);
				}
			}
			else if (Operator.empty())//栈空就入栈
			{
				Operator.push(e);
			}
			//操作符的优先级高于栈顶操作符，入栈
			else if ((e == '*' || e == '/') && (Operator.top() == '+' || Operator.top() == '-'))
			{
				Operator.push(e);
			}
			else//操作符的优先级低于或等于栈顶操作符则出栈，直至栈空或者优先级高于栈顶操作符
			{
				while (!Operator.empty())
				{
					operand.push_back(Operator.top());
					Operator.pop();
				}
				Operator.push(e);
			}
		}
		//操作数
		else
		{
			operand.push_back(e);
		}
	}
	while (!Operator.empty())
	{
		operand.push_back(Operator.top());
		Operator.pop();
	}
	return operand;
}

int evalRPN(const string& s)
{
	stack<char> operand;
	int left = 0, right = 0;
	for (const auto& e : s)
	{
		if (e == '+' || e == '-' || e == '*' || e == '/')
		{
			switch (e)
			{
			case '+':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left + right);
				break;
			case '-':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left - right);
				break;
			case '*':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left * right);
				break;
			case '/':
				right = operand.top();
				operand.pop();
				left = operand.top();
				operand.pop();
				operand.push(left / right);
				break;
			}
		}
		else//操作数
		{
			operand.push(e - '0');
		}
	}
	return operand.top();
}

int RPN(const string& str)
{
	//1.中缀表达式转化为后缀表达式
	string s(str);
	s = trans(s);
	//2.后缀表达式计算答案
	return evalRPN(s);
}

int main()
{
	string s("1*(2*3+5)/5-4/2");
	int ret = RPN(s);
	cout << "ret:" << ret << endl;
	return 0;
}

结果:

到此这篇关于C++栈实现逆波兰式的应用的文章就介绍到这了,更多相关C++ 逆波兰式内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！