漫画讲解C语言中最近公共祖先的三种类型

最近公共祖先定义

查找最近公共祖先

三叉链

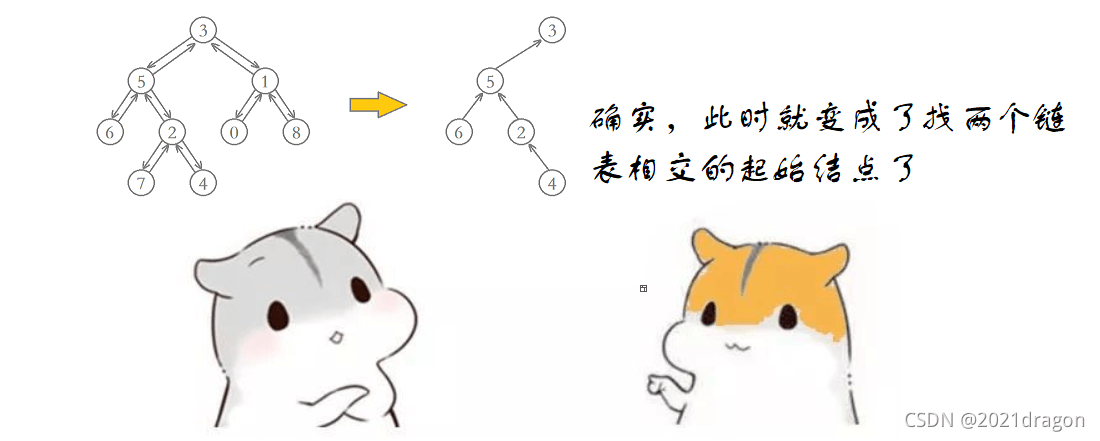
代码如下：

//三叉链
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
	TreeNode *parent;
    TreeNode(int x) : val(x), left(NULL), right(NULL), parent(NULL) {}
};
class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		TreeNode* curp = p, *curq = q; //用于遍历p、q结点的祖先结点
		int lenp = 0, lenq = 0; //分别记录p、q结点各自的祖先结点个数
		//统计p结点的祖先结点个数
		while (curp != root)
		{
			lenp++;
			curp = curp->parent;
		}
		//统计q结点的祖先结点个数
		while (curq != root)
		{
			lenq++;
			curq = curq->parent;
		}
		//longpath和shortpath分别标记祖先路径较长和较短的结点
		TreeNode* longpath = p, *shortpath = q;
		if (lenp < lenq)
		{
			longpath = q;
			shortpath = p;
		}
		//p、q结点祖先结点个数的差值
		int count = abs(lenp - lenq);
		//先让longpath往上走count个结点
		while (count--)
		{
			longpath = longpath->parent;
		}
		//再让longpath和shortpath同时往上走，此时第一个相同的结点便是最近公共祖先结点
		while (longpath != shortpath)
		{
			longpath = longpath->parent;
			shortpath = shortpath->parent;
		}
		return longpath; //返回最近公共祖先结点
	}
};

二叉搜索树

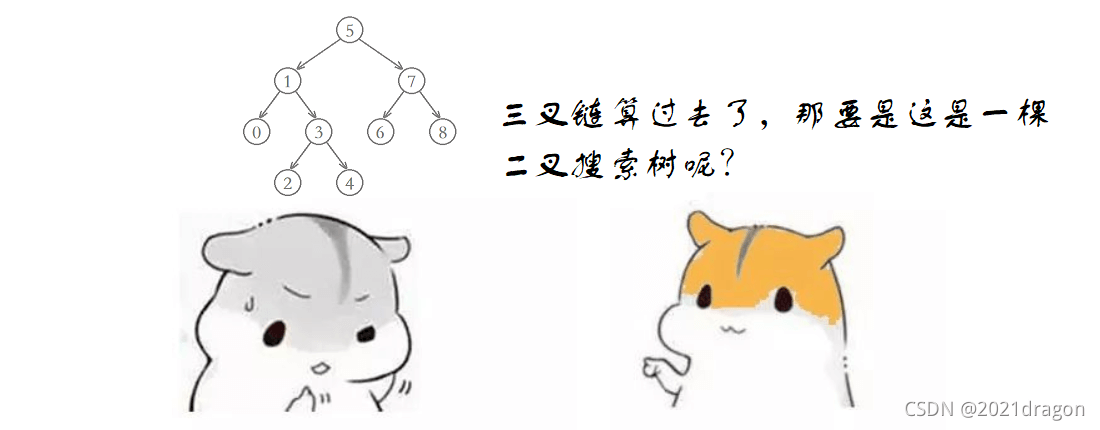
代码如下：

//搜索二叉树
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		if (p->val == root->val || q->val == root->val) //p、q结点中某一个结点的值等于根结点的值，则根结点就是这两个结点的最近公共祖先
			return root;
		if (p->val < root->val&&q->val < root->val) //p、q结点的值都小于根结点的值，说明这两个结点的最近公共祖先在该树的左子树当中
			return lowestCommonAncestor(root->left, p, q);
		else if (p->val > root->val&&q->val > root->val) //p、q结点的值都大于根结点的值，说明这两个结点的最近公共祖先在该树的右子树当中
			return lowestCommonAncestor(root->right, p, q);
		else //p、q结点的值一个比根小一个比根大，说明根就是这两个结点的最近公共祖先
			return root;
	}
};

普通二叉树

代码如下：

//普通二叉树
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
	bool Find(TreeNode* root, TreeNode* x)
	{
		if (root == nullptr) //空树，查找失败
			return false;
		if (root == x) //查找成功
			return true;

		return Find(root->left, x) || Find(root->right, x); //在左子树找到了或是右子树找到了，都说明该结点在该树当中
	}
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		if (p == root || q == root) //p、q结点中某一个结点为根结点，则根结点就是这两个结点的最近公共祖先
			return root;
		//判断p、q结点是否在左右子树
		bool IspInLeft, IspInRight, IsqInLeft, IsqInRight;
		IspInLeft = Find(root->left, p);
		IspInRight = !IspInLeft;
		IsqInLeft = Find(root->left, q);
		IsqInRight = !IsqInLeft;

		if (IspInLeft&&IsqInLeft) //p、q结点都在左子树，说明这两个结点的最近公共祖先也在左子树当中
			return lowestCommonAncestor(root->left, p, q);
		else if (IspInRight&&IsqInRight) //p、q结点都在右子树，说明这两个结点的最近公共祖先也在右子树当中
			return lowestCommonAncestor(root->right, p, q);
		else //p、q结点一个在左子树一个在右子树，说明根就是这两个结点的最近公共祖先
			return root;
	}
};

看着似乎不太好理解，来看看下面的动图演示：

代码如下：

//普通二叉树
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
	bool FindPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
	{
		if (root == nullptr)
			return false;
		path.push(root); //该结点可能是路径当中的结点，先入栈

		if (root == x) //该结点是最终结点，查找结束
			return true;

		if (FindPath(root->left, x, path)) //在该结点的左子树找到了最终结点，查找结束
			return true;
		if (FindPath(root->right, x, path)) //在该结点的右子树找到了最终结点，查找结束
			return true;

		path.pop(); //在该结点的左右子树均没有找到最终结点，该结点不可能是路径当中的结点，该结点出栈
		return false; //在该结点处查找失败
	}
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		stack<TreeNode*> pPath, qPath;
		FindPath(root, p, pPath); //将从根到p结点的路径存放到pPath当中
		FindPath(root, q, qPath); //将从根到q结点的路径存放到qPath当中
		//longpath和shortpath分别标记长路径和短路径
		stack<TreeNode*>* longPath = &pPath, *shortPath = &qPath;
		if (pPath.size() < qPath.size())
		{
			longPath = &qPath;
			shortPath = &pPath;
		}
		//让longPath先弹出差值个数据
		int count = longPath->size() - shortPath->size();
		while (count--)
		{
			longPath->pop();
		}
		//longPath和shortPath一起弹数据，直到两个栈顶的结点相同
		while (longPath->top() != shortPath->top())
		{
			longPath->pop();
			shortPath->pop();
		}
		return longPath->top(); //返回这个相同的结点，即最近公共祖先
	}
};

到此这篇关于漫画讲解C语言中最近公共祖先的三种类型的文章就介绍到这了,更多相关C语言 公共祖先内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！