浅谈numpy 中dot()函数的计算方式

如下所示：

a = np.arange(1, 5).reshape(2, 2)
b = np.arange(2, 6).reshape(2, 2)
c = a * b
dot = np.dot(a, b)
print(a)
print(b)
print(c)
print(dot)

打印出a

[[1 2]

[3 4]]

打印出b

[[2 3]

[4 5]]

a * b 每个相对位置的数值相乘1*2=2,2*3=6,3*4=12,4*5=20.比较简单,自己脑补一下

[[ 2 6]

[12 20]]

a.dot(b)也可以下成下面的那种形式,看你喜欢了.关键是算法

np.dot(a,b)

[[10 13]

[22 29]]

10=1*2+2*4 a[1][1]*b[1][1]+a[1][2]*b[2][1]

13=1*3+2*5

22=3*2+4*4

29=3*3+4*5 a[2][1]*b[1][2]+a[2][2]*b[2][2]

就这样了，规律自己找~

补充：Numpy矩阵乘积函数（dot）运算规则解析

np.dot(A, B)

A为二维m*n的举证，B必须为n*l的矩阵，l两个矩阵的n必须一致，也就是说A有多少列，B就必须有多少行，否则无法运算。结果得到m*l的矩阵

m*l = np.dot(m*n,n*l),m n l指维度，得到m*l的矩阵

运算顺序如下图：

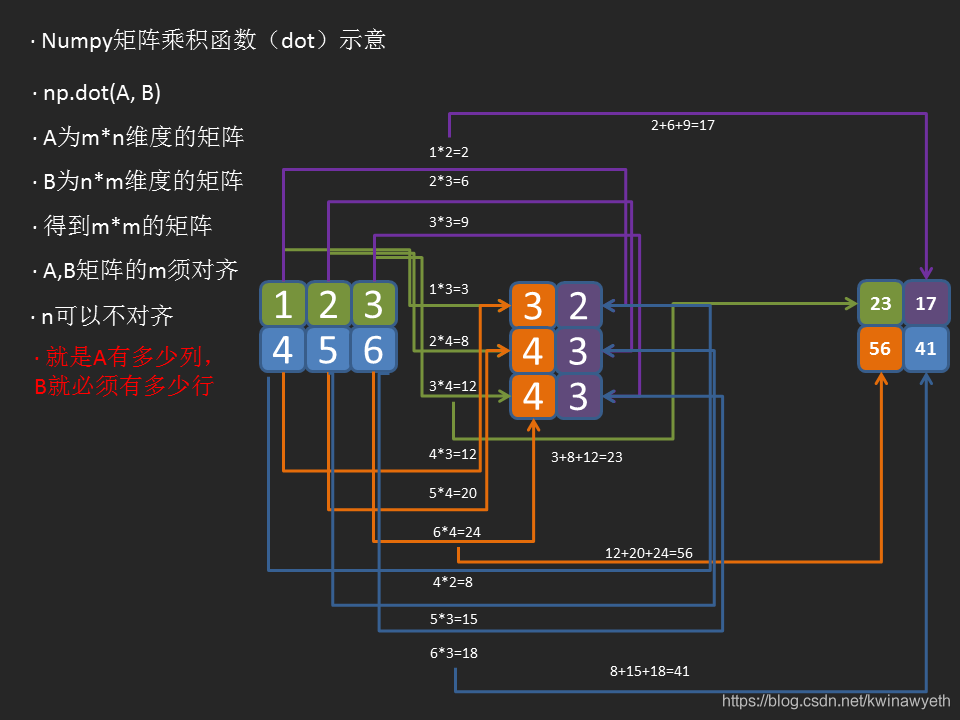
程序演示如下：

import numpy as np
A = [[1, 2, 3], [4, 5, 6]]
B = [[3, 2], [4, 3], [4, 3]]
print(np.dot(A, B))

结果：

[[23 17]

[56 41]]

如果A和B的形状交换会怎么样呢？

import numpy as np
A = [[1, 2, 3], [4, 5, 6]]
B = [[3, 2], [4, 3], [4, 3]]
print(np.dot(B, A))

结果是这样哟！不是说形状一定是变小哟

[[11 16 21]

[16 23 30]

[16 23 30]]

这是A和B的形状不一样：

import numpy as np
A = [[1, 2, 3], [4, 5, 6]]
B = [[3], [4], [4]]
print(np.dot(A, B))

结果如下：

[[23]

[56]]

以上为个人经验，希望能给大家一个参考，也希望大家多多支持我们。如有错误或未考虑完全的地方，望不吝赐教。

赞 (0)

相关推荐

  • python3 numpy中数组相乘np.dot(a,b)运算的规则说明

    python3 numpy中数组相乘np.dot(a,b)运算的规则说明

    python np.dot(a,b)运算规则解析 首先我们知道dot运算时不满足交换律的,np.dot(a, b)与np.dot(b, a)是不一样的 另外np.dot(a,b)和a.dot(b)果是一样的 1.numpy中数组相乘np.dot(a,b)运算条件: 对于两数组a和b : 示例一: a = np.array([[3], [3], [3]]) # (3,1) b = np.array([2, 2, 1]) # (3,) print(a, "\na的shape", a.sha

  • numpy中np.nditer、flags=[''multi_index''] 的用法说明

    numpy中np.nditer、flags=[''multi_index''] 的用法说明

    在看CS231n的时候,有这么一行代码 it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite']) 查了查np.nditer原来是numpy array自带的迭代器.这里简单写个demo解释一下np.nditer的用法. 先构建一个3x4的矩阵 然后输入命令 flags=['multi_index']表示对a进行多重索引,具体解释看下面的代码. op_flags=['readwrite']表示不仅可以对a进行read(读取),

  • Python基础之Numpy的基本用法详解

    一.数据生成 1.1 手写数组 a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) # 一维数组 b = np.array([[1, 2], [3, 4]]) #二维数组 1.2 序列数组 numpy.arange(start, stop, step, dtype),start默认0,step默认1 c = np.arange(0, 10, 1, dtype=int) # =np.arange(10) [0 1 2 3 4 5 6 7 8 9] d

  • nditer—numpy.ndarray 多维数组的迭代操作

    nditer—numpy.ndarray 多维数组的迭代操作

    1. Single array iteration >>> a = np.arange(6).reshape(2,3) >>> for x in np.nditer(a): ... print x, ... 0 1 2 3 4 5 也即默认是行序优先(row-major order,或者说是 C-order),这样迭代遍历的目的在于,实现和内存分布格局的一致性,以提升访问的便捷性: >>> for x in np.nditer(a.T): ... pr

  • numpy 实现返回指定行的指定元素的位置索引

    numpy 实现返回指定行的指定元素的位置索引

    先上代码,主要语句为np.where(b[c]==1), 详细解释如下: import numpy as np b = np.array([[-2,-3,0,0,0,6,4,1],[88,1,0,0,0,6,4,2],[99,6,0,0,1,6,4,2]]) # 三行八列的数组b print('b\n',b) c = np.array([2,0]) # c表示指定行 print('b[c]\n',b[c]) # b[c]返回 数组b的指定行 这里依次返回了b的下标为2和0的行 print('\n

  • Python利用numpy实现三层神经网络的示例代码

    Python利用numpy实现三层神经网络的示例代码

    本文主要介绍了Python利用numpy实现三层神经网络的示例代码,分享给大家,具体如下: 其实神经网络很好实现,稍微有点基础的基本都可以实现出来.主要都是利用上面这个公式来做的. 这是神经网络的整体框架,一共是三层,分为输入层,隐藏层,输出层.现在我们先来讲解下从输出层到到第一个隐藏层. 使用的编译器是jupyter notebook import numpy as np #定义X,W1,B1 X = np.array([1.0, 0.5]) w1 = np.array([[0.1, 0.3,

  • Python基础之numpy库的使用

    numpy库概述 numpy库处理的最基础数据类型是由同种元素构成的多维数组,简称为"数组" 数组的特点: 数组中所有元素的类型必须相同 数组中元素可以用整数索引 序号从0开始 ndarray类型的维度叫做轴,轴的个数叫做秩 numpy库的解析 由于numpy库中函数较多而且容易与常用命名混淆,建议采用如下方法引用numpy库 import numpy as np numpy库中常用的创建数组函数 函数 描述 np.array([x,y,z],dtype=int) 从Python列表和

  • 浅谈numpy 中dot()函数的计算方式

    浅谈numpy 中dot()函数的计算方式

    如下所示: a = np.arange(1, 5).reshape(2, 2) b = np.arange(2, 6).reshape(2, 2) c = a * b dot = np.dot(a, b) print(a) print(b) print(c) print(dot) 打印出a [[1 2] [3 4]] 打印出b [[2 3] [4 5]] a * b 每个相对位置的数值相乘1*2=2,2*3=6,3*4=12,4*5=20.比较简单,自己脑补一下 [[ 2 6] [12 20]]

  • 浅谈numpy中linspace的用法 (等差数列创建函数)

    浅谈numpy中linspace的用法 (等差数列创建函数)

    linspace 函数 是创建等差数列的函数, 最好是在 Matlab 语言中见到这个函数的,近期在学习Python 中的 Numpy, 发现也有这个函数,以下给出自己在学习过程中的一些总结. (1)指定起始点 和 结束点. 默认 等差数列个数为 50. (2)指定等差数列个数 (3)如果数列的元素个数指定, 可以设置 结束点 状态. endpoint : bool, optional If True, stop is the last sample. Otherwise, it is not

  • 浅谈numpy中函数resize与reshape,ravel与flatten的区别

    这两组函数中区别很是类似,都是一个不改变之前的数组,一个改变数组本身 resize和reshape >>> import numpy as np >>> a = np.arange(20).reshape(4,5) >>> a array([[ 0, 1, 2, 3, 4], [ 5, 6, 7, 8, 9], [10, 11, 12, 13, 14], [15, 16, 17, 18, 19]]) >>> a.reshape(2,1

  • 浅谈Shell中的函数

    函数可以让我们将一个复杂功能划分成若干模块,让程序结构更加清晰,代码重复利用率更高.像其他编程语言一样,Shell也支持函数.Shell函数必须先定义后使用. 1.Shell函数的定义格式 可以带function关键字使用function fun_name()来定义,也可以直接给出函数名fun_name()定义.不能带任何参数,函数名必须唯一,使时可以传递参数,使用$1,$2,...,$* ,$@来获取参数.建议使用function关键字来定义函数,便于代码阅读.定义格式如下: function

  • 浅谈Javascript中的函数、this以及原型

    关于函数 在Javascript中函数实际上就是一个对象,具有引用类型的特征,所以你可以将函数直接传递给变量,这个变量将表示指向函数"对象"的指针,例如: function test(message){ alert(message); } var f = test; f('hello world'); 你也可以直接将函数申明赋值给变量: var f = function(message){ alert(message); }; f('hello world'); 在这种情况下,函数申明

  • 浅谈js中test()函数在正则中的使用

    test() 方法用于检测一个字符串是否匹配某个模式. 返回一个 Boolean 值,它指出在被查找的字符串中是否匹配给出的正则表达式. regexp.test(str) 参数 regexp 必选项.包含正则表达式模式或可用标志的正则表达式对象. str    必选项.要在其上测试查找的字符串. 说明 test 方法检查字符串是否与给出的正则表达式模式相匹配,如果是则返回 true,否则就返回 false. 每个正则表达式都有一个 lastIndex 属性,用于记录上一次匹配结束的位置. var

  • 浅谈C++中虚函数实现原理揭秘

    编译器到底做了什么实现的虚函数的晚绑定呢?我们来探个究竟. 编译器对每个包含虚函数的类创建一个表(称为V TA B L E).在V TA B L E中,编译器放置特定类的虚函数地址.在每个带有虚函数的类 中,编译器秘密地置一指针,称为v p o i n t e r(缩写为V P T R),指向这个对象的V TA B L E.通过基类指针做虚函数调 用时(也就是做多态调用时),编译器静态地插入取得这个V P T R,并在V TA B L E表中查找函数地址的代码,这样就能调用正确的函数使晚捆绑发生

  • 浅谈MySQL中group_concat()函数的排序方法

    浅谈MySQL中group_concat()函数的排序方法

    group_concat()函数的参数是可以直接使用order by排序的.666.. 下面通过例子来说明,首先看下面的t1表. 比如,我们要查看每个人的多个分数,将该人对应的多个分数显示在一起,分数要从高到底排序. 可以这样写: SELECT username,GROUP_CONCAT(score ORDER BY score DESC) AS myScore FROM t1 GROUP BY username; 效果如下: 以上这篇浅谈MySQL中group_concat()函数的排序方法就

  • 浅谈js中startsWith 函数不能在任何浏览器兼容的问题

    在做js测试的时候用到了startsWith函数,但是他并不是每个浏览器都有的,所以我们一般要重写一下这个函数,具体的用法可以稍微总结一下 在有些浏览器中他是undefined 所以我们可以这样的处理一下. if (typeof String.prototype.startsWith != 'function') { String.prototype.startsWith = function (prefix){ return this.slice(0, prefix.length) === p

  • 浅谈mysql中concat函数,mysql在字段前/后增加字符串

    MySQL中concat函数 使用方法: CONCAT(str1,str2,-) 返回结果为连接参数产生的字符串.如有任何一个参数为NULL ,则返回值为 NULL. 注意: 如果所有参数均为非二进制字符串,则结果为非二进制字符串. 如果自变量中含有任一二进制字符串,则结果为一个二进制字符串. 一个数字参数被转化为与之相等的二进制字符串格式:若要避免这种情况,可使用显式类型 cast, 例如: SELECT CONCAT(CAST(int_col AS CHAR), char_col) MySQ

随机推荐