Python Numpy库的超详细教程

2024-10-29 16:25:15

1、Numpy概述

1.1 概念

Python本身含有列表和数组，但对于大数据来说，这些结构是有很多不足的。由于列表的元素可以是任何对象，因此列表中所保存的是对象的指针。对于数值运算来说这种结构比较浪费内存和CPU资源。至于数组对象，它可以直接保存数值，和C语言的一维数组比较类似。但是由于它不支持多维，在上面的函数也不多，因此也不适合做数值运算。Numpy提供了两种基本的对象：ndarray(N-dimensional Array Object)和 ufunc(Universal Function Object)。ndarray是存储单一数据类型的多维数组，而ufunc则是能够对数组进行处理的函数。

1.2 功能

创建n维数组(矩阵)
对数组进行函数运算，使用函数计算十分快速，节省了大量的时间，且不需要编写循环，十分方便
数值积分、线性代数运算、傅里叶变换
ndarray快速节省空间的多维数组，提供数组化的算术运算和高级的广播功能。

1.3 对象

NumPy中的核心对象是ndarray
ndarray可以看成数组，存放同类元素
NumPy里面所有的函数都是围绕ndarray展开的

ndarray 内部由以下内容组成：
• 一个指向数据(内存或内存映射文件中的一块数据)的指针。
• 数据类型或 dtype，描述在数组中的固定大小值的格子。
• 一个表示数组形状(shape)的元组，表示各维度大小的元组。形状为(row×col)

1.4 数据类型

numpy 支持的数据类型比 Python 内置的类型要多很多，基本上可以和C语言的数据类型对应上主要包括int8、int16、int32、int64、uint8、uint16、uint32、uint64、float16、float32、float64

1.5 数组属性

属性	说明
ndarray.ndim	秩，即轴的数量或维度的数量
ndarray.shape	数组的维度(n×m)，对于矩阵，n 行 m 列
ndarray.size	数组元素的总个数，相当于 .shape 中 n*m 的值
ndarray.dtype	ndarray 对象的元素类型
ndarray.itemsize	ndarray 对象中每个元素的大小，以字节为单位
ndarray.flags	ndarray 对象的内存信息
ndarray.real	ndarray元素的实部
ndarray.imag	ndarray元素的虚部
ndarray.data	包含实际数组元素的缓冲区，由于一般通过数组的索引获取元素，所以通常不需要使用这个属性。

2、Numpy数组操作

2.1 Numpy创建

2.1.1 利用列表生成数组

import numpy as np

lst = [1, 2, 3, 4]
nd1 = np.array(lst)
print(nd1, type(nd1))
#[1 2 3 4] <class 'numpy.ndarray'>

2.1.2 利用random模块生成数组

下面是random模块的一些常用函数
::: hljs-center

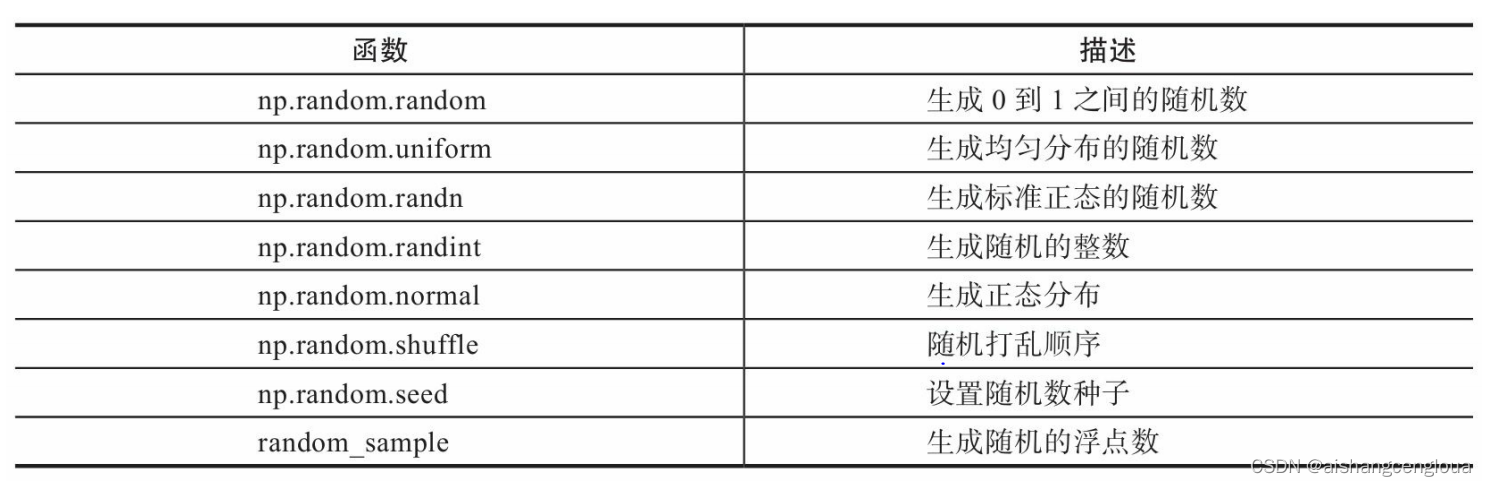
使用如下：

import numpy as np
#0到1标准正态分布
arr1 = np.random.randn(3, 3)
#0到1均匀分布
arr2 = np.random.rand(3, 3)
#均匀分布的随机数（浮点数），前两个参数表示随机数的范围，第三个表示生成随机数的个数
arr3 = np.random.uniform(0, 10, 2)
#均匀分布的随机数（整数），前两个参数表示随机数的范围，第三个表示生成随机数的个数
arr4 = np.random.randint(0, 10, 3)
print(f'arr1 : {arr1}\narr2 : {arr2}\narr3 : {arr3}\narr4 : {arr4}')
out :
# arr1 : [[-0.31637952 -0.08258995  1.43866984]
#  [-0.11216775  0.43881134  0.11745847]
#  [-1.1770306  -0.97657465  2.2368878 ]]
# arr2 : [[0.16350611 0.4467384  0.9465067 ]
#  [0.1882318  0.40261184 0.93577701]
#  [0.56243911 0.69179631 0.83407725]]
# arr3 : [4.41402883 6.03259052]
# arr4 : [9 7 7]

如果想使每次生成的数据相同，可以指定一个随机种子

import numpy as np
np.random.seed(123)
arr = np.random.rand(2, 3)#[[0.69646919 0.28613933 0.22685145] [0.55131477 0.71946897 0.42310646]]
#打乱数组
np.random.shuffle(arr)#[[0.55131477 0.71946897 0.42310646] [0.69646919 0.28613933 0.22685145]]

2.1.3 创建特定形状数组

主要有如下几种：

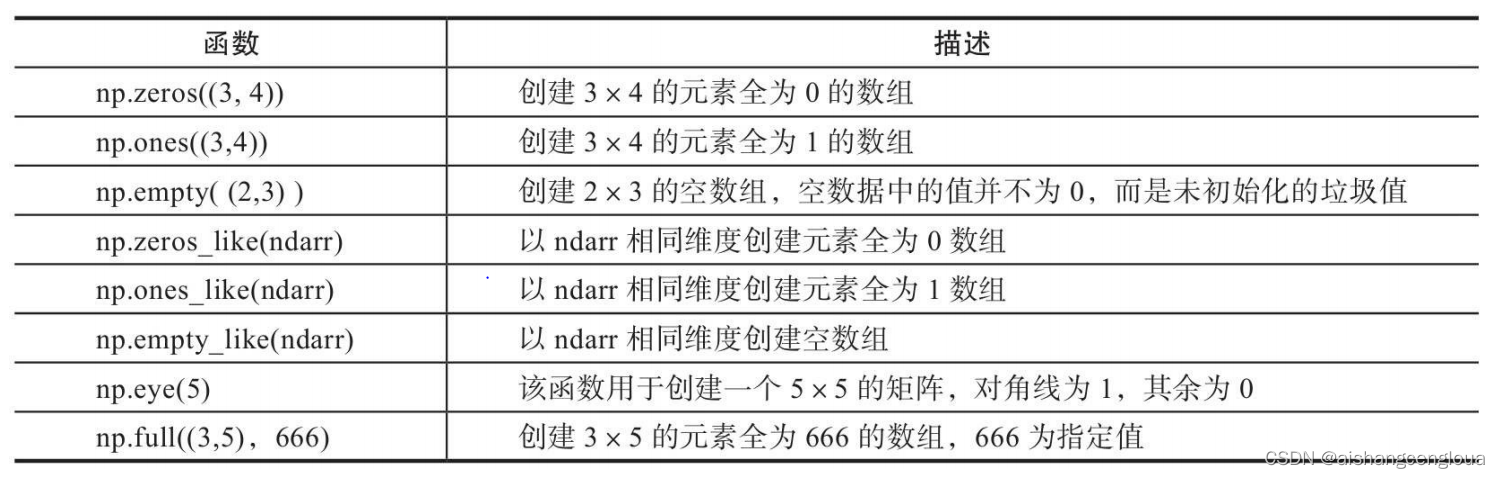
import numpy as np

#未初始化的数组
arr1 = np.empty((2,3))
#数组元素以 0 来填充
arr2 = np.zeros((2, 3))
#数组元素以 1 来填充
arr3 = np.ones((2, 3))
#数组以指定的数来进行填充，这里举例3
arr4 = np.full((2, 3), 3)
#生成单位，对角线上元素为 1，其他为0
arr5 = np.eye(2)
#二维矩阵输出矩阵对角线的元素，一维矩阵形成一个以一维数组为对角线元素的矩阵
arr6 = np.diag(np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]))

在创建给定长度的等差数列时，要注意的是np.linspace形成的数组一定包括范围的首位两个元素，则步长为(end - start) / (length - 1)。而np.arange是自己指定的步长(默认为1)也就意味着形成的数组不一定包括末尾数

arr7 = np.linspace(0, 1, 4) #out : array([0.        , 0.33333333, 0.66666667, 1.        ])
arr8 = np.arange(0, 9, 2) #out : array([0, 2, 4, 6, 8])

2.2 索引和切片

Numpy可以通过索引或切片来访问和修改，与 Python 中 list 的切片操作一样，设置start, stop 及 step 参数。

2.2.1 元素表示

Numpy数组的下标表示与list是一样的，对于矩阵来说，要注意中括号里要用逗号将行和列的表示进行分隔。基本的表示方法如下图，左边为表达式，右边为表达式获取的元素。注意，不同的边界，表示不同的表达式。

例子：
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
a[0] : 指的是第一行
a[1, 2] 或者 a[1][2] : 全下标定位单个元素，在a中表示7这个元素

2.2.2 切片表示

若a = np.arange(10)，b = a[2 : 7 : 2]则表示从索引 2 开始到索引 7 停止，间隔为 2，即b为[2, 4, 6]。此外也可以通过切片操作来对元素进行修改，如：

a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
a[0 , 1 : 3] = 100, 101#a[0 , 1 : 3]表示第一行的第二列和第二列即[2, 3]
a #out : array([[  1, 100, 101], [  4,   5,   6], [  7,   8,   9]])

2.2.3 多维数组的切片

NumPy的多维数组和一维数组类似。多维数组有多个轴。从内到外分别是第0轴，第1轴，第2轴......切片后的数据与切片前的数据共享原数组的储存空间

当然，切片操作是针对我们想要获取的数据是连续的，如果我们想要获取离散数据就不能使用切片的方法，再者就是我们不能一个一个来进行提取，Numpy有一种很方便的方法可以获得离散数据。即下面

x = np.array([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])
rows = np.array( [ [0,0],[3,3] ] ) #表示第1、4行
cols = np.array( [ [0,2],[0,2] ] ) #表示第1、3列
y = x[rows,cols]
y # out : array([[ 0,  2], [ 9, 11]])

2.2.4 布尔索引

顾名思义，通过布尔运算（如：比较运算符）来获取符合指定条件的元素的数组。

x = np.array([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])
print(x[x > 5]) # out : [ 6  7  8  9 10 11]
b = x > 5
b # 打印布尔运算的结果

2.2.5 元素查找定位

Numpy库中提供了where函数来查找满足条件元素的索引，表示如下：

np.where(condition, x, y): 满足条件(condition)，输出x，不满足输出y
np.where(condition): 输出满足条件 (即非0) 元素的坐标

a = np.array([2,4,6,8,10,3]).reshape(2,3)
c = np.where(a > 5) # 返回索引 out : (array([0, 1, 1], dtype=int64), array([2, 0, 1], dtype=int64))
a[c] # 获得元素

2.2.6 元素删除

np.delete(arr, obj, axis=None)

第一个参数：要处理的矩阵，
第二个参数，处理的位置，下标
第三个参数，0表示按照行删除，1表示按照列删除，默认为0
返回值为删除后的剩余元素构成的矩阵

arr = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
np.delete(arr, [1], 0) # 表示删除第二行

2.3 Numpy数组的拼接和分割

2.3.1 拼接

下面的图列举了常见的用于数组或向量合并的方法。

说明：

append、concatenate以及stack都有一个axis参数，用于控制数组的合并方式是按行还是按列。
对于append和concatenate，待合并的数组必须有相同的行数或列数
stack、hstack、dstack，要求待合并的数组必须具有相同的形状

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
np.hstack((a,b)) #等效于 np.concatenate((a,b),axis = 1)
# out : array([[1, 2, 5, 6], [3, 4, 7, 8]])

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
np.vstack((a,b)) #等价于 np.concatenate((a,b),axis = 0)
# out : array([[1, 2], [3, 4], [5, 6], [7, 8]])

2.3.2 分割

水平分割：np.split(arr,n,axis=1) 或 np.hsplit(arr,n)：按列分成n份。返回一个list
垂直分割：np.split(arr,n,axis=0) 或 np.vsplit(arr,n)：按行分成n份，返回一个list

x = np.arange(12).reshape(3, 4)
np.split(x, 3) # out : [array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8,  9, 10, 11]])]

y = np.arange(9).reshape(1, 9)
np.split(y, 3, axis = 1) # out : [array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])]

2.4 维度变换

在机器学习以及深度学习的任务中，通常需要将处理好的数据以模型能接收的格式输入给模型，然后由模型通过一系列的运算，最终返回一个处理结果。然而，由于不同模型所接收的输入格式不一样，往往需要先对其进行一系列的变形和运算，从而将数据处理成符合模型要求的格式。在矩阵或者数组的运算中，经常会遇到需要把多个向量或矩阵按某轴方向合并，或展平 (如在卷积或循环神经网络中，在全连接层之前，需要把矩阵展平)的情况。下面介绍几种常用的数据变形方法。

1) reshape 不改变原数组元素，返回一个新的shape维度的数组(维度变换)

x = np.arange(12).reshape(3, 4)
x # out : array([[ 0,  1,  2,  3], [ 4,  5,  6,  7], [ 8,  9, 10, 11]])

# 指定维度时可以只指定行数或列数, 其他用 -1 代替
x.reshape(3, -1) # out : array([[ 0,  1,  2,  3], [ 4,  5,  6,  7], [ 8,  9, 10, 11]])

2) resize 改变向量的维度(修改向量本身)：

arr =np.arange(10)
print(arr) # out : [0 1 2 3 4 5 6 7 8 9]

arr.resize(2, 5) # 将向量 arr 维度变换为2行5列
print(arr) # out : [[0 1 2 3 4], [5 6 7 8 9]]

3) T 转置

arr = np.arange(8).reshape(2, 4)
arr.shape # out : (2, 4)
arr.T.shape # out : (4, 2)

4) ravel 向量展平

arr = np.arange(8).reshape(2, 4)
arr.ravel() # out : array([0, 1, 2, 3, 4, 5, 6, 7])

5) flatten 把矩阵转换为向量，这种需求经常出现在卷积网络与全连接层之间。

arr = np.arange(8).reshape(2, 4)
arr.flatten() # out : array([0, 1, 2, 3, 4, 5, 6, 7])

6) squeeze 这是一个主要用来降维的函数，把矩阵中含1的维度去掉

arr = np.arange(8).reshape(2, 4, 1)
arr.shape # out : (2, 4, 1)
arr.squeeze().shape # out : (2, 4)

7) transpose 对高维矩阵进行轴对换，这个在深度学习中经常使用，比如把图片中表示颜色顺序的RGB改为GBR。

arr = np.arange(12).reshape(2, 6, 1)
arr.shape # out : (2, 6, 1)
arr.transpose(1, 2, 0).shape # out : (6, 1, 2)

拓展8) swapaxes 将两个维度调换, 就是把对应的下标换个位置，类似于transpose

arr = np.arange(20).reshape(4, 5)
arr.swapaxes(1, 0)

2.5 Numpy数值计算

2.5.1 通用函数对象(ufunc)

ufunc是universal function的简称，种能对数组每个元素进行运算的函数。NumPy的许多ufunc函数都是用C语言实现的，因此它们的运算速度非常快。下图是在数据批量处过程中较为常用的几个函数

使用的格式基本如下：np.函数名(数组，指定计算的维度(默认为0))，如：

a = np.array([[6, 3, 7, 4, 6], [9, 2, 6, 7, 4], [3, 7, 7, 2, 5], [4, 1, 7, 5, 1]])
np.sum(a, axis = 0) # out : array([22, 13, 27, 18, 16])
np.sum(a, axis = 1)# out : array([26, 28, 24, 18]

其余函数使用过程均可参考上述求和过程。下面继续介绍一下数组的排序问题。主要使用函数有np.min，np.max，np.median。

arr = np.array([[10, 11, 12], [13, 14, 15]])
np.min(arr, axis = 0) # out : array([10, 11, 12]) 按行求最小值，即列不变，行变
np.min(arr, axis = 1) # out : array([10, 13]) 按列求最小值，即行不变，列变

我们可以通过np.argmin，np.argmax获得相对应的最小值、最大值的下标

arr = np.array([[10, 14, 12], [13, 11, 15]])
np.argmin(arr, axis = 0) # out : array([0, 1, 0], dtype=int64) 按行求最小值，即列不变，行变
np.argmin(arr, axis = 1) # out : array([0, 1], dtype=int64) 按列求最小值，即行不变，列变

使用np.sort和np.argsor进行排序并排序后的下标

arr = np.array([1, 3, 5, 2, 4])
np.sort(arr) # out : array([1, 2, 3, 4, 5])
np.argsort(arr) # out : array([0, 3, 1, 4, 2], dtype=int64)

2.5.2 矩阵运算

1) 对应元素相乘 对应元素相乘（Element-Wise Product）是两个矩阵中对应元素乘积。 np.multiply函数用于数组或矩阵对应元素相乘，输出与相乘数组或矩阵的大小一致。

a = np.array([[1,0],[0,1]])
b = np.array([[4,1],[2,2]])
np.multiply(a, b) # 等效于a * b，out : array([[4, 0], [0, 2]])

计算过程如下图：

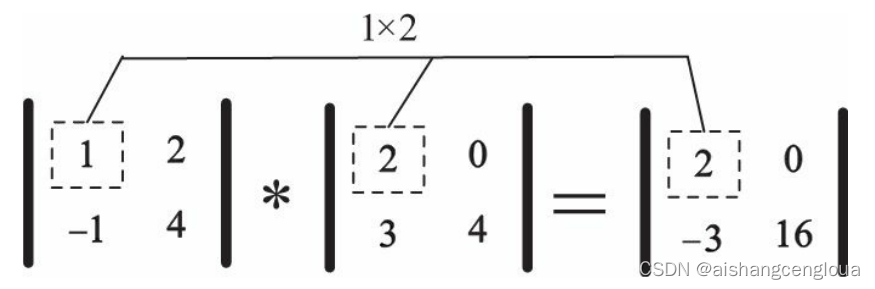
2) 点积 点积运算(Dot Product)又称为内积，在Numpy用np.dot或者np.matmul表示

a = np.array([[1,0],[0,1]])
b = np.array([[4,1],[2,2]])
np.dot(a, b) # 等效于np.matmul(a, b) out : array([[4, 1], [2, 2]])

计算过程如下图：

3) 行列式 计算行列式的值

arr = np.array([[1,2], [3,4]])
np.linalg.det(arr) # out : -2.0000000000000004

4) 求逆

arr = np.array([[1,2], [3,4]])
np.linalg.inv(arr) # out : array([[-2. ,  1. ], [ 1.5, -0.5]])

5) 特征值和特征向量

A = np.random.randint(-10,10,(4,4))
C = np.dot(A.T, A)
vals, vecs = np.linalg.eig(C)
print(f'特征值 : {vals}, 特征向量 : {vecs}')
out :
特征值 : [395.26566729 358.52489695  44.41465068  52.79478508]
特征向量 : [[ 0.30221599  0.64309202 -0.64757004 -0.27522935]
             [ 0.87819925 -0.03518532  0.18871425  0.43808105]
             [-0.35779498  0.26192443 -0.27010759  0.85464626]
             [ 0.09702746 -0.71874212 -0.68708214  0.04374437]]

2.6 插值运算

这个过程其实就是我们在数学中已知一个函数，然后给出x值，让你根据这个函数求对应的y值，一般在曲线平滑处理中有较多的使用在Numpy中由numpy.interp(x, xp, fp, left=None, right=None, period=None)表示

x - 表示将要计算的插值点x坐标
xp - 表示已有的xp数组
fp - 表示对应于已有的xp数组的值

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 2 * np.pi, 10)
y = np.sin(x)

xvals = np.linspace(0, 2 * np.pi, 10000)
yinterp = np.interp(xvals, x, y)

plt.plot(x, y, 'r-', xvals, yinterp, 'b-')
plt.show()

::: hljs-center

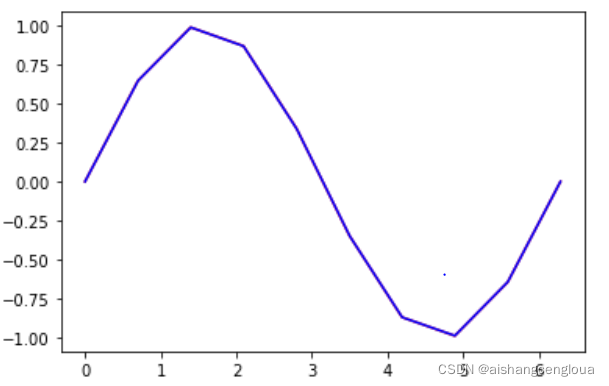
2.7 曲线拟合

我们在数学建模过程中得到我们的数据之后，如果我们想要使用某个函数去描述数据的规律，这个过程其实就在曲线拟合的过程，这里只介绍最简单的一种拟合方式。Numpy中由numpy.polyfit(x, y, deg)表示

x为待拟合的x坐标
y为待拟合的y坐标
deg为拟合自由度，即多项式的最高次幂

import matplotlib.pyplot as plt
import numpy as np

x = np.array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0])
y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0])
#得到多项式的系数
z = np.polyfit(x, y, 3)
z2 = np.polyfit(x, y, 5)
#得到多项式函数
f = np.poly1d(z)
f2 = np.poly1d(z2)
#用两个函数进行拟合
xval = np.linspace(0, 10, 50)
yval1 = f(xval)
yval2 = f2(xval)
#作图
plt.plot(xval, yval1, 'r--o', xval, yval2, 'b-o')
plt.legend(['The deg is 3', 'The deg is 5'])
plt.show()

print(f) # out :  0.08704 x^3 - 0.8135 x^2 + 1.693 x - 0.03968
print(f2) # out : -0.008333 x^5 + 0.125 x^4 - 0.575 x^3 + 0.625 x^2 + 0.6333 x - 1.74e-14