Java数据结构之线段树详解

目录

• 介绍
• 代码实现
• 线段树构建
• 区间查询
• 更新
• 总结

介绍

线段树(又名区间树)也是一种二叉树，每个节点的值等于左右孩子节点值的和，线段树示例图如下

以求和为例，根节点表示区间0-5的和，左孩子表示区间0-2的和，右孩子表示区间3-5的和，依次类推。

代码实现

/**
 * 使用数组实现线段树
 */
public class SegmentTree<E> {

  private Node[] data;
  private int size;

  private Merger<E> merger;

  public SegmentTree(E[] source, Merger<E> merger) {
    this.merger = merger;
    this.size = source.length;
    this.data = new Node[size * 4];
    buildTree(0, source, 0, size - 1);
  }

  public E search(int queryLeft, int queryRight) {
    if (queryLeft < 0 || queryLeft > size || queryRight < 0 || queryRight > size
        || queryLeft > queryRight) {
      throw new IllegalArgumentException("index is illegal");
    }
    return search(0, queryLeft, queryRight);
  }

  /**
   * 查询区间queryLeft-queryRight的值
   */
  private E search(int treeIndex, int queryLeft, int queryRight) {
    Node treeNode = data[treeIndex];
    int left = treeNode.left;
    int right = treeNode.right;
    if (left == queryLeft && right == queryRight) {
      return elementData(treeIndex);
    }
    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    int middle = left + ((right - left) >> 1);
    if (queryLeft > middle) {
      return search(rightTreeIndex, queryLeft, queryRight);
    } else if (queryRight <= middle) {
      return search(leftTreeIndex, queryLeft, queryRight);
    }
    E leftEle = search(leftTreeIndex, queryLeft, middle);
    E rightEle = search(rightTreeIndex, middle + 1, queryRight);
    return merger.merge(leftEle, rightEle);
  }

  public void update(int index, E e) {
    update(0, index, e);
  }

  /**
   * 更新索引为index的值为e
   */
  private void update(int treeIndex, int index, E e) {
    Node treeNode = data[treeIndex];
    int left = treeNode.left;
    int right = treeNode.right;
    if (left == right) {
      treeNode.data = e;
      return;
    }
    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    int middle = left + ((right - left) >> 1);
    if (index > middle) {
      update(rightTreeIndex, index, e);
    } else {
      update(leftTreeIndex, index, e);
    }
    treeNode.data = merger.merge(elementData(leftTreeIndex), elementData(rightTreeIndex));
  }

  private void buildTree(int treeIndex, E[] source, int left, int right) {
    if (left == right) {
      data[treeIndex] = new Node<>(source[left], left, right);
      return;
    }
    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    int middle = left + ((right - left) >> 1);
    buildTree(leftTreeIndex, source, left, middle);
    buildTree(rightTreeIndex, source, middle + 1, right);
    E treeData = merger.merge(elementData(leftTreeIndex), elementData(rightTreeIndex));
    data[treeIndex] = new Node<>(treeData, left, right);
  }

  @Override
  public String toString() {
    return Arrays.toString(data);
  }

  private E elementData(int index) {
    return (E) data[index].data;
  }

  private int leftChild(int index) {
    return index * 2 + 1;
  }

  private int rightChild(int index) {
    return index * 2 + 2;
  }

  private static class Node<E> {

    E data;
    int left;
    int right;

    Node(E data, int left, int right) {
      this.data = data;
      this.left = left;
      this.right = right;
    }

    @Override
    public String toString() {
      return String.valueOf(data);
    }
  }

  public interface Merger<E> {

    E merge(E e1, E e2);
  }
}

我们以LeetCode上的一个问题来分析线段树的构建，查询和更新，LeetCode307问题如下：

给定一个整数数组，查询索引区间[i,j]的元素的总和。

线段树构建

private void buildTree(int treeIndex, E[] source, int left, int right) {
    if (left == right) {
      data[treeIndex] = new Node<>(source[left], left, right);
      return;
    }
    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    int middle = left + ((right - left) >> 1);
    buildTree(leftTreeIndex, source, left, middle);
    buildTree(rightTreeIndex, source, middle + 1, right);
    E treeData = merger.merge(elementData(leftTreeIndex), elementData(rightTreeIndex));
    data[treeIndex] = new Node<>(treeData, left, right);
  }

测试代码

public class Main {

  public static void main(String[] args) {
    Integer[] nums = {-2, 0, 3, -5, 2, -1};
    SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, Integer::sum);
    System.out.println(segmentTree);
  }

}

最后构造出的线段树如下，前面为元素值，括号中为包含的区间。

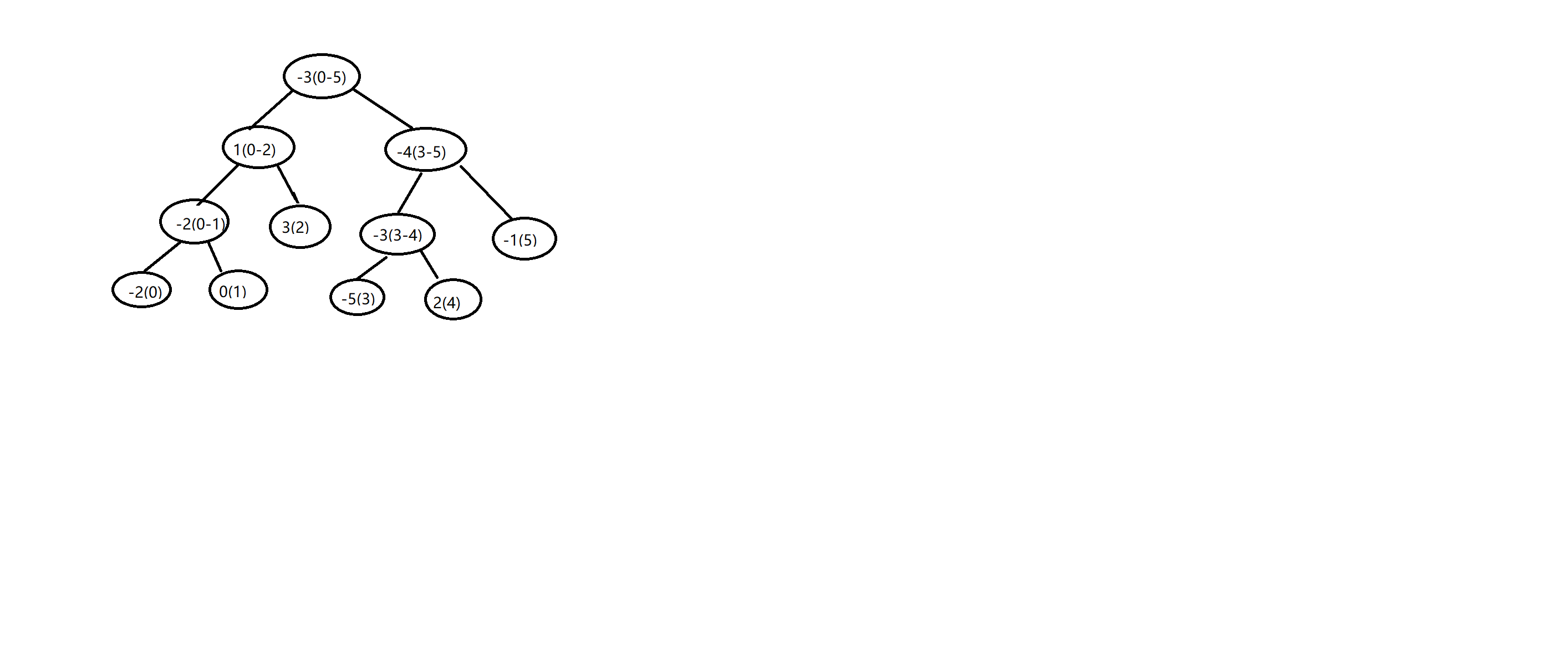
递归构造过程为

• 当左指针和右指针相等时，表示为叶子节点
• 将左孩子和右孩子值相加，构造当前节点，依次类推

区间查询

  /**
   * 查询区间queryLeft-queryRight的值
   */
  private E search(int treeIndex, int queryLeft, int queryRight) {
    Node treeNode = data[treeIndex];
    int left = treeNode.left;
    int right = treeNode.right;
    if (left == queryLeft && right == queryRight) {
      return elementData(treeIndex);
    }
    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    int middle = left + ((right - left) >> 1);
    if (queryLeft > middle) {
      return search(rightTreeIndex, queryLeft, queryRight);
    } else if (queryRight <= middle) {
      return search(leftTreeIndex, queryLeft, queryRight);
    }
    E leftEle = search(leftTreeIndex, queryLeft, middle);
    E rightEle = search(rightTreeIndex, middle + 1, queryRight);
    return merger.merge(leftEle, rightEle);
  }

查询区间2-5的和

public class Main {

  public static void main(String[] args) {
    Integer[] nums = {-2, 0, 3, -5, 2, -1};
    SegmentTree<Integer> segmentTree = new SegmentTree<>(nums, Integer::sum);
    System.out.println(segmentTree);
    System.out.println(segmentTree.search(2, 5)); // -1
  }

}

查询过程为

• 待查询的区间和当前节点的区间相等，返回当前节点值
• 待查询左区间大于中间区间值，查询右孩子
• 待查询右区间小于中间区间值，查询左孩子
• 待查询左区间在左孩子，右区间在右孩子，两边查询结果相加

更新

  /**
   * 更新索引为index的值为e
   */
  private void update(int treeIndex, int index, E e) {
    Node treeNode = data[treeIndex];
    int left = treeNode.left;
    int right = treeNode.right;
    if (left == right) {
      treeNode.data = e;
      return;
    }
    int leftTreeIndex = leftChild(treeIndex);
    int rightTreeIndex = rightChild(treeIndex);
    int middle = left + ((right - left) >> 1);
    if (index > middle) {
      update(rightTreeIndex, index, e);
    } else {
      update(leftTreeIndex, index, e);
    }
    treeNode.data = merger.merge(elementData(leftTreeIndex), elementData(rightTreeIndex));
  }

更新只影响元素值，不影响元素区间。

更新其实和构建的逻辑类似，找到待更新的实际索引，依次更新父节点的值。

总结

线段树可以很好地处理区间问题，如区间求和，求最大最小值等。

以上就是Java 数据结构之线段树详解的详细内容，更多关于Java 线段树的资料请关注我们其它相关文章！