Python光学仿真数值分析求解波动方程绘制波包变化图

波动方程数值解

波动方程是三大物理方程之一，也就是弦振动方程，其特点是时间与空间均为二阶偏导数。其自由空间解便是我们熟知的三角函数形式，也可以写成自然虚指数形式。

一般来说，既然有了精确的解析解，那也就没必要再去做不精确的数值模拟，但数值模拟的好处有两个，一是避免无穷小，从而在思维上更加直观；二是颇具启发性，对于一些解析无解的情况也有一定的处理能力。

对此，我们首先考虑一维波动方程

import numpy as np
import matplotlib.pyplot as plt
def set_y0(x,k,L):
    y = np.zeros_like(x)
    y[x<L] = np.sin(k*x[x<L])*np.sin(np.abs(x[x<L]*np.pi/L))
    return y

if __name__ == "__main__":
    x = np.linspace(0,10,1000)
    k = np.pi*2/1.064
    L = 5
    y = set_y0(x,k,L)

    plt.plot(x,y)
    plt.show()

其形状为

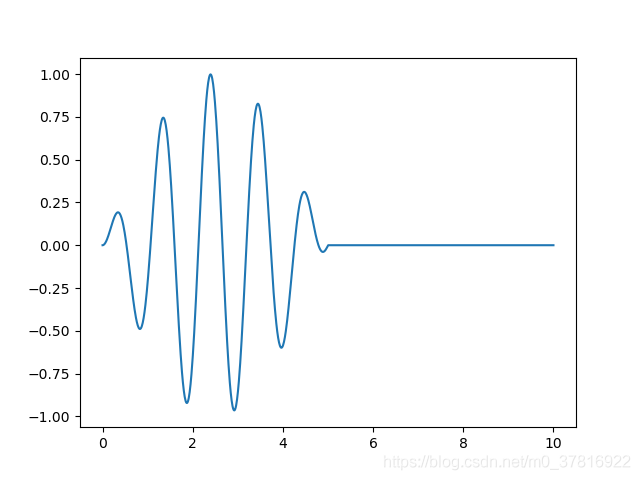
现考虑让这个光波在 [ 0 , L ] 范围内往返传播，在此采用Dirichlet边界条件，取

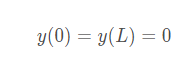
至此，我们得到了光场的所有信息，原则上可以预测这个波包的所有行为，其迭代过程为

def wave1d(x,t,k,L):
    dx = x[1]-x[0]
    dt = t[1]-t[0]
    d2 = (dt/dx)**2
    y = np.zeros([len(t),len(x)])
    y[0,:] = set_y0(x,k,L)
    y[1,:] = set_y0(x-dt,k,L)
    for n in range(2,len(t)):
        y[n] = 2*y[n-1] - y[n-2] - d2*2*y[n-1]
        y[n,1:] += d2*y[n-1,:-1]
        y[n,:-1] += d2*y[n-1,1:]
        #边界条件
        y[n,0] = 0
        y[n,-1] = 0
    return y

由于 y y y是随时间变化的参量，现有的matplotlib.pyplot已经无法满足我们绘制动态图片的需求，所以引入animation来进行绘制，其代码为

import matplotlib.animation as animation
#输入时间，自变量，因变量，图题标记
def drawGif(t,x,ys,mark="time="):
    tAxis = np.linspace(0,len(t)-1,100).astype(int)
    fig = plt.figure()
    ax = fig.add_subplot(111,xlim=(0,10),ylim=(-1.5,1.5))
    ax.grid()
    line, = ax.plot([],[],lw=0.2)
    time_text = ax.text(0.1,0.9,'',transform=ax.transAxes)
    def init():
        line.set_data([],[])
        time_text.set_text("")
        return line, time_text
    def animate(i):
        y = ys[i]
        line.set_data(x,y)
        time_text.set_text(mark+str(t[i]))
        return line, time_text
    # 动态图绘制命令
    # 输入分别为画图窗口，动画函数，动画函数输入变量，延时，初始函数
    ani = animation.FuncAnimation(fig, animate, tAxis,
        interval=200, init_func=init)
    #通过imagemagick引擎来保存gif
    ani.save('wave.gif',writer='imagemagick')
    plt.show()
if __name__ == "__main__":
    x = np.linspace(0,10,1000)
    t = np.linspace(0,12,2041)
    k = np.pi*2/1.064
    L = 5
    y = wave1d(x,t,k,L)
    drawGif(t,x,y)

得到结果为

这个图虽然很符合我们的预期，但有些物理过程并不清晰，我们不妨把初始波包设置为只有一个波峰的孤波

def set_y0(x,k,L):
    y = np.zeros_like(x)
    y[x<L] = np.sin(np.abs(x[x<L]*np.pi/L))
    return y

其图像为

我们可以清晰地看到，正弦波通过腔壁后，其震动方向发生了变化，此即半波损失。

以上就是Python光学仿真数值分析求解波动方程绘制波包变化图的详细内容，更多关于Python数值分析求解波动方程绘制波包变化图的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • Python线性方程组求解运算示例

    Python线性方程组求解运算示例

    本文实例讲述了Python线性方程组求解运算.分享给大家供大家参考,具体如下: 求解线性方程组比较简单,只需要用到一个函数(scipy.linalg.solve)就可以了.比如我们要求以下方程的解,这是一个非齐次线性方程组: 3x_1 + x_2 - 2x_3 = 5 x_1 - x_2 + 4x_3 = -2 2x_1 + 3x_3 = 2.5 代码如下: # coding=utf-8 import numpy as np from scipy.linalg import solve a =

  • Python光学仿真之对光的干涉理解学习

    Python光学仿真之对光的干涉理解学习

    光的干涉 干涉即两束光在叠加过程中出现的强度周期性变化情况,其最简单的案例即为杨氏双缝干涉. 如图所示,光从 S S S点发出,通过两个狭缝 S 1 , S 2 S_1,S_2 S1​,S2​,最终汇聚在右侧的干涉屏上,在不同位置处将会产生不同的相位差. import numpy as np import matplotlib.pyplot as plt #两束光叠加 waveAdd = lambda I1,I2,theta : I1+I2+2*np.sqrt(I1*I2)*np.cos(the

  • Python光学仿真光的偏振编程理解学习

    Python光学仿真光的偏振编程理解学习

    目录 光的偏振 光的偏振 由于光波是横波,所以对于任意一个光波,其振幅方向与传播方向在一个固定的平面内.换言之,一束光波可以存在振幅方向不同的一群光波,对于其中一个光波而言,其振幅方向即为偏振方向. 可以画出其示意图 #偏振光演示 import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D as axd def polarShow(): z = np.arange(0,5,0

  • Python光学仿真实现波长与颜色之间对应关系示例解析

    Python光学仿真实现波长与颜色之间对应关系示例解析

    目录 光的颜色 python实现为 绘制光谱 光的颜色 与其说颜色是光的一种属性,不如说是人眼对可见光频率范围内的一种感应,是人眼的一种属性.而人眼对光频的感应包括三个方面,即明度.色调和饱和度. 其中, 明度与光强有关 色调反应的是光的频率信息 饱和度表示图像上的颜色与光谱色的接近程度 当不考虑色调.饱和度为0的时候,只考虑明度,则色彩感消失,就是所谓的黑白图像,或者更严格地说是灰度图像. 色调与饱和度虽然反应色光的频率信息,但表现的是人眼对光的反馈特性,与光的频率是不同的物理量.其与光的频率

  • Python光学仿真学习衍射算法初步理解

    Python光学仿真学习衍射算法初步理解

    对衍射最经典的解释是Huygens-Fresnel原理,Huygens认为波阵面上每一点都会成为新的波源,这些子波源的相互干涉就形成了衍射.这显然是一种离散的观点,仿佛是专门为程序员准备的一样. 假设一束光打在一个方形孔上,这个方形孔被细分成 n×n个网格,那么每个网格都相当于是一个小孔,而这些小孔的互相干涉,即为衍射.随着网格不断被细分,最终可以逼近真实的衍射情形.那么,假设矩孔处为等相位面,其网格坐标为  (i,j),到衍射屏距离为 d d d,那么对于衍射屏上任意一点P(x,y),其光强为

  • Python光学仿真数值分析求解波动方程绘制波包变化图

    Python光学仿真数值分析求解波动方程绘制波包变化图

    波动方程数值解 波动方程是三大物理方程之一,也就是弦振动方程,其特点是时间与空间均为二阶偏导数.其自由空间解便是我们熟知的三角函数形式,也可以写成自然虚指数形式. 一般来说,既然有了精确的解析解,那也就没必要再去做不精确的数值模拟,但数值模拟的好处有两个,一是避免无穷小,从而在思维上更加直观:二是颇具启发性,对于一些解析无解的情况也有一定的处理能力. 对此,我们首先考虑一维波动方程 import numpy as np import matplotlib.pyplot as plt def se

  • Python光学仿真从Maxwell方程组到波动方程矢量算法理解学习

    Python光学仿真从Maxwell方程组到波动方程矢量算法理解学习

    Maxwell方程组是十九世纪最伟大的公式,代表了传统物理学人对公式美学的孜孜追求,也影响了无数后来者的物理美学品味. 回顾历史,当1864年,Maxwell发出那篇著名的<电磁场的动力学理论>时,实则列出了二十个公式,以总结前人的物理学成果,我们将分量公式合并为矢量,可以得到八个式子,即 以上符号分别表示 二十年后,Heaviside对这二十个公式进行重新编排,得到了我们熟悉的形式,并将其命名为麦克斯韦方程组: 对上式中左侧两个旋度公式再取旋度,得到 其中, ∇ E = 0,所以可得到波动方

  • Python光学仿真教程实现光线追踪

    Python光学仿真教程实现光线追踪

    目录 光线追迹 几何抽象 光线 线段与圆弧 光线追迹 得益于计算机的计算的能力,通过追踪具有代表性的光线的传播轨迹,可以更加精确地描述光学系统的性能,光线追迹方法也因此大展其能,诸如Zemax.tracepro等软件便都提供了相应的功能. 而建立在折射定律基础之上的光线追迹方法,对数学功底要求较低,所以比较适合作为python初学者的入门项目.在接下来的这一章,希望通过对光线追迹的实现,掌握python中的列表.元组.字典.集合等数据类型的基本概念,并且对面向对象与函数式编程有一个基本的了解.

  • python光学仿真通过菲涅耳公式实现波动模型

    python光学仿真通过菲涅耳公式实现波动模型

    从物理学的机制出发,波动模型相对于光线模型,显然更加接近光的本质:但是从物理学的发展来说,波动光学旨在解决几何光学无法解决的问题,可谓光线模型的一种升级.从编程的角度来说,波动光学在某些情况下可以简单地理解为在光线模型的基础上,引入一个相位项. 波动模型 一般来说,三个特征可以确定空间中的波场:频率.振幅和相位,故光波场可表示为: import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import

  • Python光学仿真wxpython透镜演示系统计算与绘图

    目录 计算与绘图 计算与绘图 这里的计算主要包括两个部分,分别是通过滚动条的参数得到光学器件的特征,这一点此前已经备述.其二则是光在传播过程中所产生的各种行为,反射折射函数也都已经讲过了,需要注意的就是确定边界. def getRay(self): self.rays,self.abcs,self.dots = [[],[],[]] sDot = self.source #光源为第一个点 sRay = rp.getABC(self.sourceDict['theta'],sDot) inPoin

  • Python光学仿真wxpython透镜演示系统初始化与参数调节

    Python光学仿真wxpython透镜演示系统初始化与参数调节

    初始化与参数调节面板 这一节将绘制出如下图所示的参数调节面板 对于上图来说,BoxSizer布局十分傻瓜,所以这里主要有两个方面需要注意,其一是opti和source这两个选项卡的实现,其二则是如何同时创建多个滚动条. 对于前者比较容易,无非是多用一个控件而已,即wx.NoteBook,使用方法乏善可陈,看代码即可学会. 对于后者当然也可以很容易,只要无脑罗列即可,只不过对于五个不同的参数就意味着要新建五组滚动条,要就要新建五个控制函数,而这五个控制函数的功能几乎是完全一样的.显然,这很愚蠢,所

  • Python光学仿真wxpython透镜演示系统框架

    透镜演示系统 框架 现在,我们可以做一个具备友好界面的透镜演示系统了.我们需要两个圆弧来表示透镜,一条线段表示主光轴,多条线段表示光线的传播路径.此外,还需要对光源和透镜的参数进行调节. 然而值得注意的一点是,我们在进行计算和画图过程中所用到的几何图形,在表达形式以及操作流程上可能并不相同.例如,对于光源发出的一条射线,它与透镜的作用流程为 寻找与透镜前表面的交点A 获取反射和透射直线 寻找透射直线与透镜后表面的交点B 计算透过透镜的直线 然而对于画图程序来说,光源S和A之间有一条线段,A和B之

  • python光学仿真实现光线追迹之空间关系

    python光学仿真实现光线追迹之空间关系

    目录 空间关系 相交判定 射线排序 线弧关系 点弧关系 空间关系 变化始于相遇,所以交点是一切的核心. 相交判定 首先考察一束光线能否打在某个平面镜上.光线被抽象成了一个列表[a,b,c],平面镜则被抽象成为由两个点构成的线段[(x1,y1),(x2,y2)].两条直线的交点问题属于初等数学范畴,需要先将线段转换成直线的形式,然后再求交点.但是两条直线的交点可能落在线段的外面,从而不具有判定的意义. 如果我们的光学系统中有大量的光学元件,那么如果有一种方法可以快速判断光线是否与光学元件有交点,将

  • python光学仿真实现光线追迹折射与反射的实现

    python光学仿真实现光线追迹折射与反射的实现

    目录 折射与反射 平面反射 平面折射 python实现 弧面问题 折射与反射 光线与光学元件相互作用,无非只有两件事,反射和透射.而就目前看来,我们所常用的光学元件,也无非有两种表面,即平面和球面,二维化之后就简化成了射线与线段,射线与劣弧的关系. 平面反射 无论从哪个角度来看,平面的反射折射都要比球面更简单,而反射问题要比折射问题更简单,所以,我们首先处理平面的反射问题. 反射定律即入射角等于反射角,心念及此,最为循规蹈矩的思路必然是先找到入射光线和平面的夹角,然后用这个夹角和平面(在二维空间

  • Python光学仿真学习处理高斯光束分布图像

    Python光学仿真学习处理高斯光束分布图像

    目录 通过python处理光斑图像 1 相关包与图像读取 2 图像截取 3显示强度 4数据拟合 问题 通过python处理光斑图像 1 相关包与图像读取 首先需要科学计算必备包numpy和画图包matplotlib.pyplot,我们通过后者进行图像数据的读取. plt.imread读取图片之后为数据格式为numpy数组,可以通过成员函数astype将整型数据变成浮点型,有利于后期处理. plt.imshow将img的数据加载到窗口,plt.show()显示绘图窗口,默认显示为伪彩图. pyth

随机推荐