Spectral clustering谱聚类算法的实现代码

目录

• 1.作者介绍
• 2.关于谱聚类的介绍
• 2.1 谱聚类概述
• 2.2 无向权重图
• 2.3 邻接矩阵
• 2.4 相似矩阵
• 2.5 度矩阵
• 2.6 拉普拉斯矩阵
• 2.7 K-Means
• 3.Spectral clustering（谱聚类）算法实现
• 3.1 数据集
• 3.2 导入所需要的包
• 3.3 获取特征值和特征向量
• 3.4 利用K-Means聚类
• 3.5 完整代码
• 4.参考

1.作者介绍

刘然，女，西安工程大学电子信息学院，2021级研究生
研究方向：图像处理
电子邮件：1654790996@qq.com

刘帅波，男，西安工程大学电子信息学院，2021级研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：1461004501@qq.com

2.关于谱聚类的介绍

2.1 谱聚类概述

谱聚类是从图论中演化出来的算法，它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

2.2 无向权重图

对于一个图G，我们一般用点的集合V和边的集合E来描述。即为G(V,E)。其中V即为我们数据集里面所有的点(v1,v2,…vn)。对于V中的任意两个点，点vi和点vj，我们定义权重wij为二者之间的权重。由于是无向图，所以wij=wji。

2.3 邻接矩阵

邻接矩阵(Adjacency Matrix):是表示顶点之间相邻关系的矩阵。在如图2-1所示的权重图当中（假设各权重为1），其邻接矩阵可表示为图2-2所示。

2.4 相似矩阵

在谱聚类中，我们只有数据点的定义，并没有直接给出这个邻接矩阵，所以我们可以通过样本点距离度量的相似矩阵S来获得邻接矩阵W。

2.5 度矩阵

度矩阵是对角阵，对角上的元素为各个顶点的度。图2-1的度矩阵为图2-3所示。

2.6 拉普拉斯矩阵

拉普拉斯矩阵L=D-W，其中D为度矩阵，W为邻接矩阵。图2-1的拉普拉斯矩阵为图2-4所示。

用拉普拉斯矩阵求解特征值，通过确定特征值（特征值要遵循从小到大的排列方式）的个数来确定对应特征向量的个数，从而实现降维，然后再用kmeans将特征向量进行聚类。

2.7 K-Means

K-Means是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快，但是只能应用于连续型的数据，并且一定要在聚类前需要手工指定要分成几类。
下面，我们描述一下K-means算法的过程，为了尽量不用数学符号，所以描述的不是很严谨，大概就是这个意思，“物以类聚、人以群分”：
1.首先输入k的值，即我们希望将数据集经过聚类得到k个分组。
2.从数据集中随机选择k个数据点作为初始大哥（质心，Centroid）
3.对集合中每一个小弟，计算与每一个大哥的距离（距离的含义后面会讲），离哪个大哥距离近，就跟定哪个大哥。
4.这时每一个大哥手下都聚集了一票小弟，这时候召开人民代表大会，每一群选出新的大哥（其实是通过算法选出新的质心）。
5.如果新大哥和老大哥之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，算法终止。
6.如果新大哥和老大哥距离变化很大，需要迭代3~5步骤。

3.Spectral clustering（谱聚类）算法实现

3.1 数据集

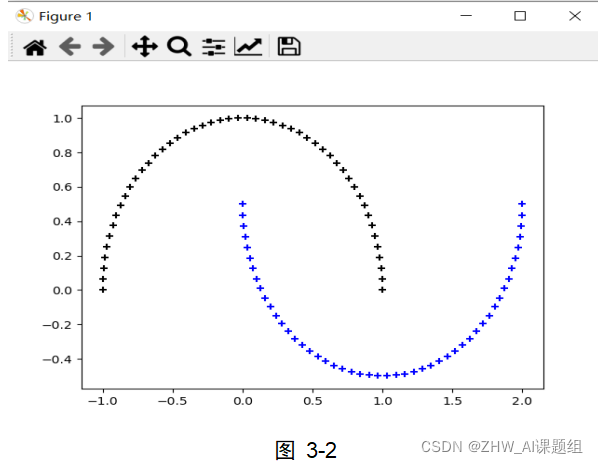
本实验中使用到的数据集均由sklearn.datasets中提供的方法生成，本实验中用到了make_circles，make_moons，make_blobs等函数。make_circles生成数据集，形成一个二维的大圆，包含一个小圆，如图3-1所示；make_moons生成数据集，形成两个弯月，如图3-2所示；make_blobs为聚类生成符合正态分布的数据集，如图3-3所示。

3.2 导入所需要的包

#导入需要的包
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons#生成数据集，形成两个弯月。
from sklearn.datasets import make_circles#生成数据集，形成一个二维的大圆，包含一个小圆
from sklearn.datasets import make_blobs#为聚类生成符合正态分布的数据集，产生一个数据集和相应的标签
import matplotlib.pyplot as plt

3.3 获取特征值和特征向量

def get_eigen(L, num_clusters):#获取特征
    eigenvalues, eigenvectors = np.linalg.eigh(L)#获取特征值  特征向量
    best_eigenvalues = np.argsort(eigenvalues)[0:num_clusters]#argsort函数返回的是数组值从小到大的索引值
    U = np.zeros((L.shape[0], num_clusters))
    U = eigenvectors[:, best_eigenvalues]#将这些特征取出 构成新矩阵
    return U

3.4 利用K-Means聚类

#K-Means聚类
def cluster(data, num_clusters):
    data = np.array(data)
    W = affinity_matrix(data)
    D = getD(W)
    L = getL(D, W)
    eigenvectors = get_eigen(L, num_clusters)
    clf = KMeans(n_clusters=num_clusters)
    s = clf.fit(eigenvectors)  # 聚类
    label = s.labels_
    return label

3.5 完整代码

#导入需要的包
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons#生成数据集，形成两个弯月。
from sklearn.datasets import make_circles#生成数据集，形成一个二维的大圆，包含一个小圆
from sklearn.datasets import make_blobs#为聚类生成符合正态分布的数据集，产生一个数据集和相应的标签
import matplotlib.pyplot as plt

#定义高斯核函数
def kernel(x1, x2, sigma_sq=0.05):
    return np.exp(-(np.linalg.norm(x1 - x2) ** 2) / (2 * sigma_sq ** 2))

#定义相似度矩阵
def affinity_matrix(X):
    A = np.zeros((len(X), len(X)))#零矩阵
    for i in range(len(X) - 1):#长度为len(x) 但是从0开始
        for j in range(i + 1, len(X)):#从1开始，到len(x) 是方阵 为啥下角标取值的初始值不同？？？
            A[i, j] = A[j, i] = kernel(X[i], X[j])
    return A#通过高斯核的计算 给矩阵赋予新值    10*10

# 计算度矩阵
def getD(A):
    D = np.zeros(A.shape)
    for i in range(A.shape[0]):
        D[i, i] = np.sum(A[i, :])
    return D

#计算拉普拉斯矩阵
def getL(D, A):
    L = D - A
    return L

def get_eigen(L, num_clusters):#获取特征
    eigenvalues, eigenvectors = np.linalg.eigh(L)#获取特征值  特征向量
    best_eigenvalues = np.argsort(eigenvalues)[0:num_clusters]#argsort函数返回的是数组值从小到大的索引值
    U = np.zeros((L.shape[0], num_clusters))
    U = eigenvectors[:, best_eigenvalues]#将这些特征取出 构成新矩阵
    return U

#K-Means聚类
def cluster(data, num_clusters):
    data = np.array(data)
    W = affinity_matrix(data)
    D = getD(W)
    L = getL(D, W)
    eigenvectors = get_eigen(L, num_clusters)
    clf = KMeans(n_clusters=num_clusters)
    s = clf.fit(eigenvectors)  # 聚类
    label = s.labels_
    return label

def plotRes(data, clusterResult, clusterNum):
    """
    结果可似化
    : data:  样本集
    : clusterResult: 聚类结果
    : clusterNum: 聚类个数
    :return:
    n = len(data)
    scatterColors = ['black', 'blue', 'red', 'yellow', 'green', 'purple', 'orange']
    for i in range(clusterNum):
        color = scatterColors[i % len(scatterColors)]
        x1 = []
        y1 = []
        for j in range(n):
            if clusterResult[j] == i:
                x1.append(data[j, 0])
                y1.append(data[j, 1])
        plt.scatter(x1, y1, c=color, marker='+')

if __name__ == '__main__':
# # #月牙形数据集,sigma=0.1
# #     # cluster_num = 2
# #     # data, target = make_moons()
# #     # label = cluster(data, cluster_num)
# #     # print(label)
# #     # plotRes(data, label, cluster_num)
# #
#     # 圆形数据集,sigma=0.05
    cluster_num = 2
    data, target = make_circles(n_samples=1000, shuffle=True, noise=0.05, factor=0.5)
    label = cluster(data, cluster_num)
    print(label)
    plotRes(data, label, cluster_num)
# #    #  # 正态数据集
# #    # # n_samples是待生成的样本的总数。
# #    #  # n_features是每个样本的特征数。
# #    #  # centers表示类别数。
# #    #  # cluster_std表示每个类别的方差，例如我们希望生成2类数据，其中一类比另一类具有更大的方差，可以将cluster_std设置为[1.0, 3.0]。
# #    #  cluster_num = 2
# #    #  data, target = make_blobs(n_samples=1500, n_features=2, centers=4, random_state=24)
# #    #  label = cluster(data, cluster_num)
# #    #  print(label)
# #    #  plt.subplot(121)
# #    #  plotRes(data, target, cluster_num)
# #    #  plt.subplot(122)
# #    #  plotRes(data, label, cluster_num)
plt.show()

4.参考

1.<谱聚类（spectral clustering）原理总结 - 刘建平Pinard - 博客园
2.参考博客1
3.参考博客2
4.参考博客3

到此这篇关于Spectral clustering谱聚类算法的实现的文章就介绍到这了,更多相关Spectral clustering谱聚类算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！