C语言深入探索递归的特点

目录
  • 递归的认识
  • main函数可以递归吗
  • 递归核心思想讲解
  • 递归的缺点

递归的认识

基本认识：

1.首先递归的本质还是函数调用，也要形成和释放栈帧。

2.函数的调用是有成本的，这个成本在时间和空间上表现为函数栈帧的形成和销毁。

3.递归就是 不断形成栈帧和销毁的过程。

理论认识：

1.内存和cpu中的资源有限，也就决定啦，合理的递归是绝对不可以无限递归下去的。

2.递归不是什么时候都可以使用的，而是要满足自身的场景，即目标函数的子问题可以用该算法解决，本质是分治的思想。

3.递归的核心：大事化小，递归出口。

main函数可以递归吗

相信有些读者就在疑惑啦？main函数是主函数呀，这个怎么可以自己调用自己呢？

实际上，main函数本质也是函数，所以也就会形成栈帧，所以是可以自己调用自己的。

代码和运行结果如下：

int main()
{
	printf("胡杨树下\n");
	Sleep(100);//睡眠0.1秒
	main();
	return 0;
}

结果显示是可以调用的，那么我们也能过看出来，这个main函数的递归是不会自动停止的，停止时就是发生栈溢出，那么函数的栈帧是怎么形成的呢？

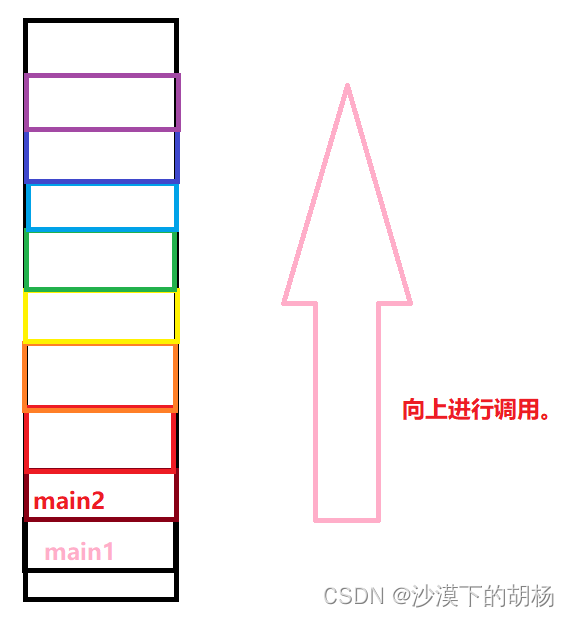
是最下面的main函数进行调用自身形成栈帧，如图示，我们可以看出，这些函数调用都开辟了空间，所以要占用内存，而且形成栈帧后需要释放，形成和释放过程中有时间消耗。这也就是递归有成本的原因。

递归核心思想讲解

我们在平时中见过这个题目，叫做求字符串长度。

这个我们可以用递归的写法求解，顺带我们看下递归的核心。

首先假设我们求的字符为 "abcdefg123"，我们用递归的解法可以转化为，1+"bcdefg123"，把"bcdefg123"进而再转化为1+"cdefg123"，进行求解，如图示：

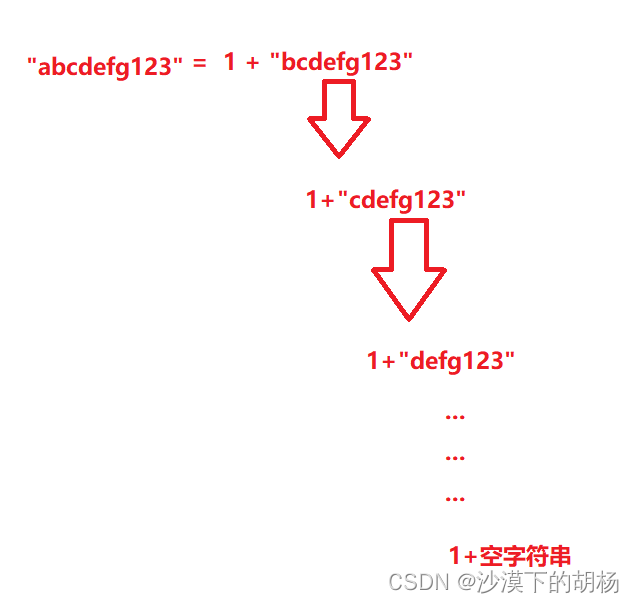
经过一次次的大事化小，我们最后把问题变成了，求1+空字符串的长度，这个其实也就是我们想要的递归出口，当没有字符时我们就该结束啦。

代码如下：

int My_strlen(const char *str)
{
	if (*str == '\0')//函数出口
	{
		return 0;
	}
	return 1 + My_strlen(str + 1);//继续
}
int main()
{
	int len = My_strlen("abcdefg123");
	printf("len = %d\n", len);
	return 0;
}

递归的缺点

我们来看下递归的另外一个经典例子，第n个菲波那切数列的实现

首先菲波那切数列是前两个数之和等于第三个数，第一个和第二个我们设定为1，那么这个数列为 1,1,2,3,5,8,13....等等，那我们要求第n个斐波那契数列的话，只要转化为求前两个数的和就好了，最后的递归出口为第一个或者第二个数时停止，结束函数。

代码如下：求第十个菲波那切数

int fib(int n)
{
	if (n == 1 || n == 2)
	{
		return 1;
	}
	return fib(n - 1) + fib(n - 2);
}
int main()
{
	printf("fib(%d) = %d\n", 10, fib(10));
	return 0;
}

我们如果求的 n 的数字比较大就会非常慢。这个本质就是上述说的成本问题。

如果求的是第42个菲波那切数呢？这次我们把时间也计算上。

int fib(int n)
{
	if (n == 1 || n == 2)
	{
		return 1;
	}
	return fib(n - 1) + fib(n - 2);
}
int main()
{
	int n = 42;
	double start = GetTickCount();
	int x = fib(n);
	double end = GetTickCount();
	printf("fib(%d) = %d count = %.1f S\n", n,x,(end - start)/1000);
	return 0;
}

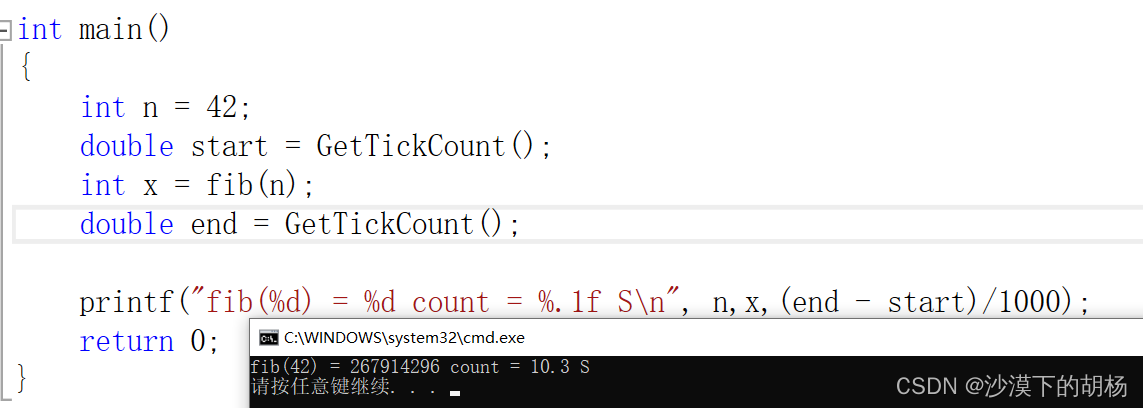
我们可以看出第42个时就已经10秒了，这个很长时间啦。我们用全局变量接收下次数，那我们看看他计算了多少次第3个菲波那切数计算了几次？ 计算了大概1亿多次，所以递归的重

复计算是非常多的。

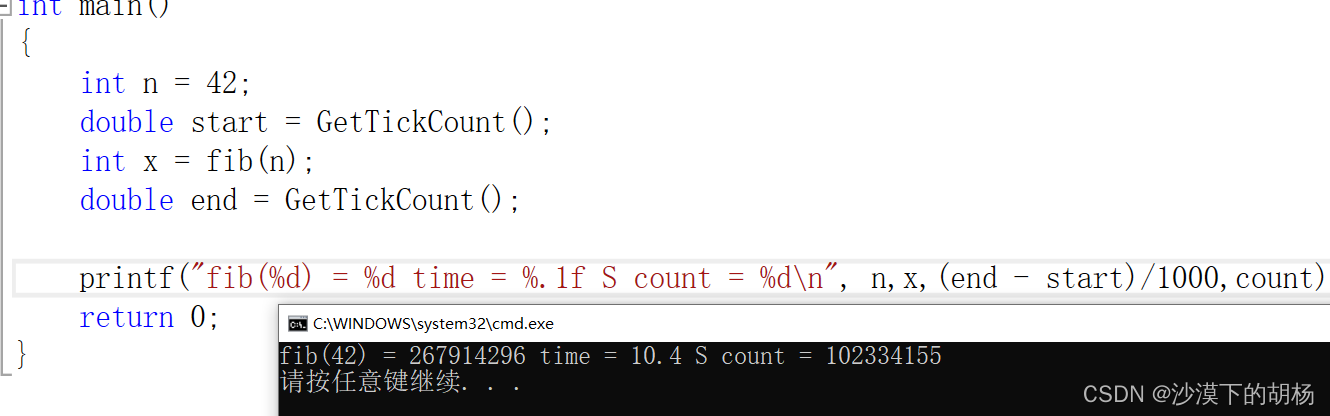
我们看个图示：

其中单单是第六个菲波那切数就计算了3次，这个就很夸张啦。

所以递归的特点是代码简单，但是调用上可能会有大的成本。

最后一点就是：循环和递归是一定可以相互转化的。只不过有些时候转化会比较麻烦。

到此这篇关于C语言深入探索递归的特点的文章就介绍到这了,更多相关C语言递归内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • 对C语言中递归算法的深入解析

    对C语言中递归算法的深入解析

    许多教科书都把计算机阶乘和菲波那契数列用来说明递归,非常不幸我们可爱的著名的老潭老师的<C语言程序设计>一书中就是从阶乘的计算开始的函数递归.导致读过这本经书的同学们,看到阶乘计算第一个想法就是递归.但是在阶乘的计算里,递归并没有提供任何优越之处.在菲波那契数列中,它的效率更是低的非常恐怖. 这里有一个简单的程序,可用于说明递归.程序的目的是把一个整数从二进制形式转换为可打印的字符形式.例如:给出一个值4267,我们需要依次产生字符'4','2','6',和'7'.就如在printf函数中使用

  • C语言编程递归算法实现汉诺塔

    C语言编程递归算法实现汉诺塔

    汉诺塔 法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针.印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔.不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面.僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔.庙宇和众生也都将同归于尽. 这个传说挺有意思的,这个传说

  • C语言超详细讲解递归算法汉诺塔

    C语言超详细讲解递归算法汉诺塔

    目录 题目描述 画图分析 思路总结 代码实现 总结 题目描述 汉诺塔问题起源于一个传说 汉诺塔又被称为河内塔,传说,在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针. 印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔. 不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面. 僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而

  • C语言之快速排序算法（递归Hoare版）介绍

    C语言之快速排序算法（递归Hoare版）介绍

    废话不多说,先看代码 #define _CRT_SECURE_NO_WARNINGS 1 //快速排序算法,递归求解 #include <stdio.h> void swap(int* a, int* b) { int c = 0; c = *a; *a = *b; *b = c; } void Compare(int arr[], int one, int end) { int first = one;//最左边数组下标 int last = end;//最右边数组下标 int key =

  • C语言程序中递归算法的使用实例教程

    C语言程序中递归算法的使用实例教程

    1.问题:计算n! 数学上的计算公式为: n!=n×(n-1)×(n-2)--2×1 使用递归的方式,可以定义为: 以递归的方式计算4! F(4)=4×F(3) 递归阶段 F(3)=3×F(2) F(2)=2×F(1) F(1)=1 终止条件 F(2)=(2)×(1) 回归阶段 F(3)=(3)×(2) F(4)=(4)×(6) 24 递归完成 以递归方式实现阶乘函数的实现: int fact(int n) { if(n < 0) return 0; else if (n == 0 || n =

  • C语言数据结构之二叉树的非递归后序遍历算法

    C语言数据结构之二叉树的非递归后序遍历算法 前言: 前序.中序.后序的非递归遍历中,要数后序最为麻烦,如果只在栈中保留指向结点的指针,那是不够的,必须有一些额外的信息存放在栈中. 方法有很多,这里只举一种,先定义栈结点的数据结构 typedef struct{Node * p; int rvisited;}SNode //Node 是二叉树的结点结构,rvisited==1代表p所指向的结点的右结点已被访问过. lastOrderTraverse(BiTree bt){ //首先,从根节点开始,

  • C语言非递归算法解决快速排序与归并排序产生的栈溢出

    C语言非递归算法解决快速排序与归并排序产生的栈溢出

    目录 1.栈溢出原因和递归的基本认识 2.快速排序(非递归实现) 3.归并排序(非递归实现) 建议还不理解快速排序和归并排序的小伙伴们可以先去看我上一篇博客​​​​​​哦!C语言超详细讲解排序算法下篇 1.栈溢出原因和递归的基本认识 我们先简单来了解下内存分布结构: 栈区:用于存放地址.临时变量等:                                                                            堆区:程序运行期间动态分配所使用的场景: 静态区

  • 用C语言递归实现火车调度算法详解

    用C语言递归实现火车调度算法详解

    目录 1.代码 2.代码详解 3.用二叉树表示调用过程 4.思维导图 笔者在李云清版的<数据结构>中第二章遇到了这道经典的火车调度题,经过对一些前辈的代码进行学习,以下将这段火车代码进行分析详解,不对之处,还请各位大佬指示,不胜感激! 1.代码 题目如下: 2.8编号为1,2,3,4的四列火车通过一个栈式的列车调度站,可能得到的调度结果有哪些?如果有n列火车通过调度站,请设计一个算法,输出所有可能的调度结果. 算法运用的思想是运用栈+递归,算法的难点也在于此.先上代码: #include &l

  • C语言深入探索递归的特点

    C语言深入探索递归的特点

    目录 递归的认识 main函数可以递归吗 递归核心思想讲解 递归的缺点 递归的认识 基本认识: 1.首先递归的本质还是函数调用,也要形成和释放栈帧. 2.函数的调用是有成本的,这个成本在时间和空间上表现为函数栈帧的形成和销毁. 3.递归就是 不断形成栈帧和销毁的过程. 理论认识: 1.内存和cpu中的资源有限,也就决定啦,合理的递归是绝对不可以无限递归下去的. 2.递归不是什么时候都可以使用的,而是要满足自身的场景,即目标函数的子问题可以用该算法解决,本质是分治的思想. 3.递归的核心:大事化小

  • C语言函数的递归和调用实例分析

    一.基本内容: C语言中的函数可以递归调用,即:可以直接(简单递归)或间接(间接递归)地自己调自己. 要点: 1.C语言函数可以递归调用. 2.可以通过直接或间接两种方式调用.目前只讨论直接递归调用. 二.递归条件 采用递归方法来解决问题,必须符合以下三个条件: 1.可以把要解决的问题转化为一个新问题,而这个新的问题的解决方法仍与原来的解决方法相同,只是所处理的对象有规律地递增或递减. 说明:解决问题的方法相同,调用函数的参数每次不同(有规律的递增或递减),如果没有规律也就不能适用递归调用. 2

  • c语言实现含递归清场版扫雷游戏

    c语言实现含递归清场版扫雷游戏

    目录 一,设计思路 二.实现方式 1.菜单的打印 2.game函数 3.棋盘的初始化与打印  4.雷的放置,雷的个数 5.递归实现一片效果  6.排查雷  三.完整代码 总结 一,设计思路 想必大家都玩过扫雷  这便是一个标准的扫雷,换做代码实现,我们需要考虑以下几点: 1.棋盘的设计与初始化 2.在棋盘中放入雷 3.统计雷数 4.如何实现"一片"的效果 5.输赢的判断 接下来我们进行具体操作. 二.实现方式 1.菜单的打印 对任意一个游戏,菜单是必不可少的,也是最简单的部分,直接上代

  • C语言深入探索浮点数的使用秘密

    C语言深入探索浮点数的使用秘密

    目录 一.内存中的浮点数 二.浮点数存储实例 三.浮点类型的秘密 四.小结 一.内存中的浮点数 浮点数在内存的存储方式为:符号位,指数,尾数 类型 符号位 指数 尾数 float 1位(第31位) 8位(第23--30位) 23位(第0--22位) double 1位(第63位) 11位(第52--62位) 52位(第0--51位) 注:float 与 double 类型的数据在计算机内部的表示法是相同的,但由于所占存储空间的不同,其分别能够表示的数值范围和精度不同. 二.浮点数存储实例 浮点数

  • C语言深入探索动态内存分配的使用

    C语言深入探索动态内存分配的使用

    目录 一.动态内存分配的意义 二.malloc 和 free 三.关于 malloc(0) 四.calloc 和 realloc 五.小结 一.动态内存分配的意义 C语言中的一切操作都是基于内存的 变量和数组都是内存的别名 内存分配由编译器在编译期间决定 定义数组的时候必须指定数组长度 数组长度是在编译期就必须确定的 需求:程序运行的过程中,可能需要使用一些额外的内存空间 二.malloc 和 free malloc 和 free 用于执行动态内存分配和释放 malloc 所分配的是一块连续的内

  • C语言函数的递归调用详情

    C语言函数的递归调用详情

    目录 一.什么是递归 二.递归与迭代 一.什么是递归 程序调用自身的编程技巧称为递归( recursion) .递归做为一种算法在程序设计语言中广泛应用.一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量.递归的主要思考方式在于:把大事化小 递归的两个必要条件: 存在限制条件,当满足这个限制条件的时候,递归便不再继续. 每次

  • C语言深入探索之单链表与typedef的用法

    C语言深入探索之单链表与typedef的用法

    目录 前言 详解typedef关键字 含义 具体使用 详解单链表参数形式 指针知识补充 单链表形参详解 单链表实战案例 完整代码实现 详解头插建表 运行效果 前言 昨天博主去本站问答贴子逛了逛,然后发现了好多关于数据结构线性表,具体来说是单链表的问题.有的是没有一点思路,无从下手:有的是看不懂代码,不理解关键字以及被形参的形式气的不行,我总结了一下常见问题来给大家带来干货,到后面还有简单案例来巩固知识,弄透一题胜无脑刷百题,接下来是正文内容. 详解typedef关键字 含义 C语言允许用户使用

  • C语言深入探索数据类型的存储

    C语言深入探索数据类型的存储

    目录 数据类型介绍 类型的基本归纳 整型家族 浮点数家族 构造类型 指针类型 空类型 整型在内存中的存储 原码,反码,补码 大小端 浮点数在内存中的存储 浮点数存储的规则 数据类型介绍 首先,对于我们C语言中的数据类型,大家应该都有一个清晰的认识吧!如果不记得也没有关系哦~ 在这里来跟着小刘同学回顾一下吧! 关于数据类型,我们在前面已经学习过了一些内置数据类型,以及它们所占的内存空间的大小,例如: char         //字符数据类型int          //整型short      

  • C语言中的递归，你真的懂了吗？

    什么是递归? 要说到递归如果不说栈的话,我觉得有点不合适,递归特点就是不断的调用同一个函数,如果这个函数没有一个递归界限,那么就是死循环了,所以讨论递归,就必须要讨论递归的界限,就是限定这个递归调用多少次. 我们看一个例子 #include "stdio.h" int digui(unsigned long count ) { if(count > 0){ count --; printf("%d \n",count); digui(count); } ret

  • Java语言实现非递归实现树的前中后序遍历总结

    Java语言实现非递归实现树的前中后序遍历总结

    前言 三种遍历的递归写法都很好写,所以总结一下非递归写法. 先贴一张图复习一下三种遍历方式就进入正文啦~ [注:本文所有代码实现中树的结点定义如下: public class Node { int val; Node left; Node right; Node parent; Node() {} Node(int val) { this.val = val; } } 1.前序遍历 实现思路: 前序遍历的顺序是:根结点 -> 左孩子 -> 右孩子 借助一个栈结构先将根结点压入栈,然后循环每次取

随机推荐