详解JAVA中priorityqueue的具体使用

Java中PriorityQueue通过二叉小顶堆实现，可以用一棵完全二叉树表示。本文从Queue接口函数出发，结合生动的图解，深入浅出地分析PriorityQueue每个操作的具体过程和时间复杂度，将让读者建立对PriorityQueue建立清晰而深入的认识。

总体介绍

前面以JavaArrayDeque为例讲解了Stack和Queue，其实还有一种特殊的队列叫做PriorityQueue，即优先队列。优先队列的作用是能保证每次取出的元素都是队列中权值最小的（Java的优先队列每次取最小元素，C++的优先队列每次取最大元素）。这里牵涉到了大小关系，元素大小的评判可以通过元素本身的自然顺序（natural ordering），也可以通过构造时传入的比较器（Comparator，类似于C++的仿函数）。

Java中PriorityQueue实现了Queue接口，不允许放入null元素；其通过堆实现，具体说是通过完全二叉树（complete binary tree）实现的小顶堆（任意一个非叶子节点的权值，都不大于其左右子节点的权值），也就意味着可以通过数组来作为PriorityQueue的底层实现。

上图中我们给每个元素按照层序遍历的方式进行了编号，如果你足够细心，会发现父节点和子节点的编号是有联系的，更确切的说父子节点的编号之间有如下关系：

leftNo = parentNo*2+1

rightNo = parentNo*2+2

parentNo = (nodeNo-1)/2

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。

PriorityQueue的peek()和element操作是常数时间，add(),offer(), 无参数的remove()以及poll()方法的时间复杂度都是log(N)。

方法剖析

add()和offer()

add(E e)和offer(E e)的语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则则会返回false。对于PriorityQueue这两个方法其实没什么差别。

新加入的元素可能会破坏小顶堆的性质，因此需要进行必要的调整。

//offer(E e)
public boolean offer(E e) {
  if (e == null)//不允许放入null元素
    throw new NullPointerException();
  modCount++;
  int i = size;
  if (i >= queue.length)
    grow(i + 1);//自动扩容
  size = i + 1;
  if (i == 0)//队列原来为空，这是插入的第一个元素
    queue[0] = e;
  else
    siftUp(i, e);//调整
  return true;
}

上述代码中，扩容函数grow()类似于ArrayList里的grow()函数，就是再申请一个更大的数组，并将原数组的元素复制过去，这里不再赘述。需要注意的是siftUp(int k, E x)方法，该方法用于插入元素x并维持堆的特性。

//siftUp()
private void siftUp(int k, E x) {
  while (k > 0) {
    int parent = (k - 1) >>> 1;//parentNo = (nodeNo-1)/2
    Object e = queue[parent];
    if (comparator.compare(x, (E) e) >= 0)//调用比较器的比较方法
      break;
    queue[k] = e;
    k = parent;
  }
  queue[k] = x;
}

新加入的元素x可能会破坏小顶堆的性质，因此需要进行调整。调整的过程为：从k指定的位置开始，将x逐层与当前点的parent进行比较并交换，直到满足x >= queue[parent]为止。注意这里的比较可以是元素的自然顺序，也可以是依靠比较器的顺序。

element()和peek()

element()和peek()的语义完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素，二者唯一的区别是当方法失败时前者抛出异常，后者返回null。根据小顶堆的性质，堆顶那个元素就是全局最小的那个；由于堆用数组表示，根据下标关系，0下标处的那个元素既是堆顶元素。所以直接返回数组0下标处的那个元素即可。

代码也就非常简洁：

//peek()
public E peek() {
  if (size == 0)
    return null;
  return (E) queue[0];//0下标处的那个元素就是最小的那个
}

remove()和poll()

remove()和poll()方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。

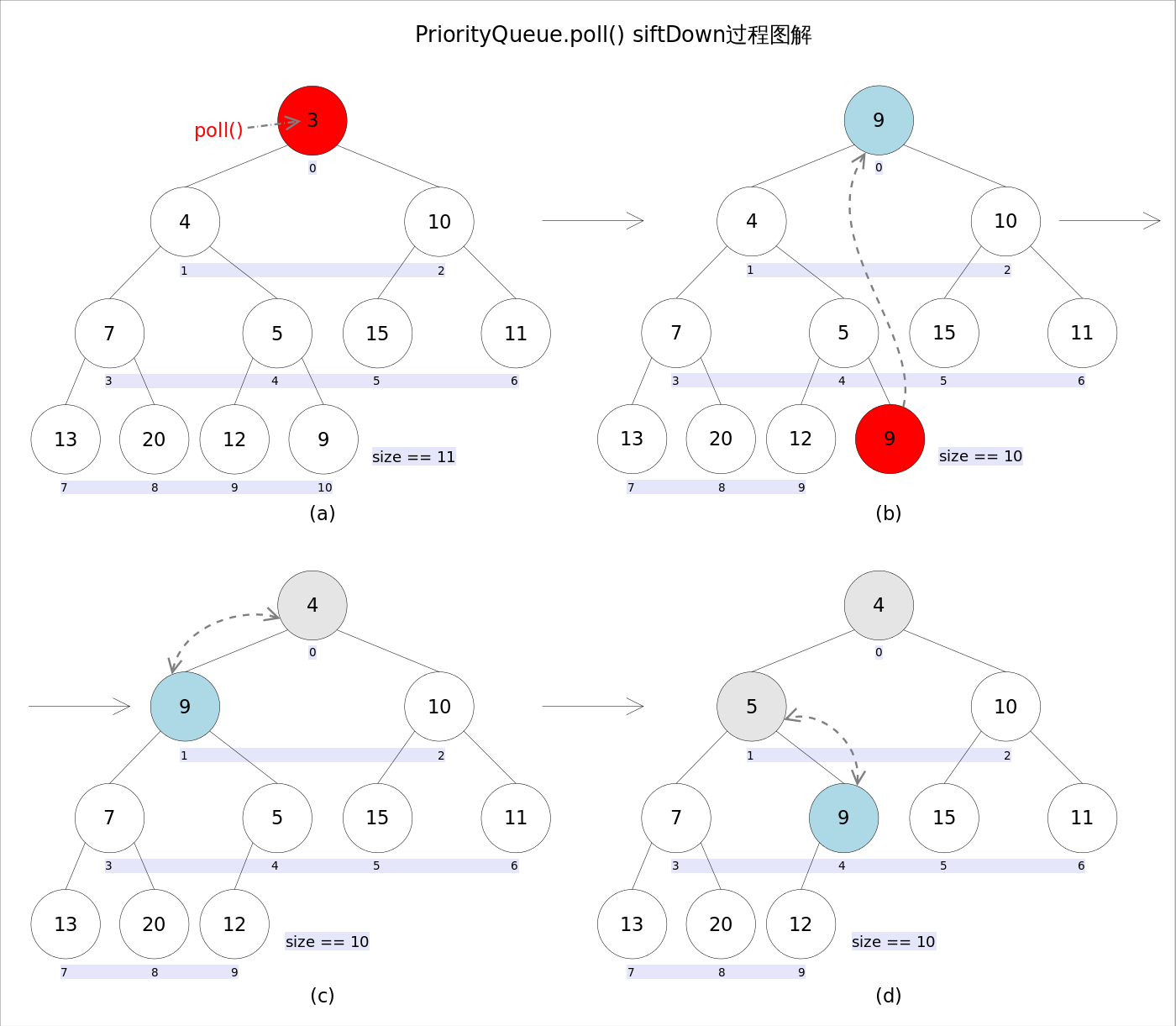
代码如下：

public E poll() {
  if (size == 0)
    return null;
  int s = --size;
  modCount++;
  E result = (E) queue[0];//0下标处的那个元素就是最小的那个
  E x = (E) queue[s];
  queue[s] = null;
  if (s != 0)
    siftDown(0, x);//调整
  return result;
}

上述代码首先记录0下标处的元素，并用最后一个元素替换0下标位置的元素，之后调用siftDown()方法对堆进行调整，最后返回原来0下标处的那个元素（也就是最小的那个元素）。重点是siftDown(int k, E x)方法，该方法的作用是从k指定的位置开始，将x逐层向下与当前点的左右孩子中较小的那个交换，直到x小于或等于左右孩子中的任何一个为止。

//siftDown()
private void siftDown(int k, E x) {
  int half = size >>> 1;
  while (k < half) {
    //首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标
    int child = (k << 1) + 1;//leftNo = parentNo*2+1
    Object c = queue[child];
    int right = child + 1;
    if (right < size &&
      comparator.compare((E) c, (E) queue[right]) > 0)
      c = queue[child = right];
    if (comparator.compare(x, (E) c) <= 0)
      break;
    queue[k] = c;//然后用c取代原来的值
    k = child;
  }
  queue[k] = x;
}

remove(Object o)

remove(Object o)方法用于删除队列中跟o相等的某一个元素（如果有多个相等，只删除一个），该方法不是Queue接口内的方法，而是Collection接口的方法。由于删除操作会改变队列结构，所以要进行调整；又由于删除元素的位置可能是任意的，所以调整过程比其它函数稍加繁琐。具体来说，remove(Object o)可以分为2种情况：1. 删除的是最后一个元素。直接删除即可，不需要调整。2. 删除的不是最后一个元素，从删除点开始以最后一个元素为参照调用一次siftDown()即可。此处不再赘述。

具体代码如下：

//remove(Object o)
public boolean remove(Object o) {
  //通过遍历数组的方式找到第一个满足o.equals(queue[i])元素的下标
  int i = indexOf(o);
  if (i == -1)
    return false;
  int s = --size;
  if (s == i) //情况1
    queue[i] = null;
  else {
    E moved = (E) queue[s];
    queue[s] = null;
    siftDown(i, moved);//情况2
    ......
  }
  return true;
}

到此这篇关于详解JAVA中priorityqueue的具体使用的文章就介绍到这了,更多相关JAVA priorityqueue内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！