Python机器学习应用之工业蒸汽数据分析篇详解

目录

• 一、数据集
• 二、数据分析
• 1 数据导入
• 2 数据特征探索（数据可视化）
• 三、特征优化
• 四、对特征构造后的训练集和测试集进行主成分分析
• 五、使用ＬｉｇｈｔＧＢＭ模型进行训练和预测

一、数据集

1. 训练集 提取码：1234

2. 测试集 提取码：1234

二、数据分析

1 数据导入

#%%导入基础包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import warnings
warnings.filterwarnings("ignore")
#%%读取数据
train_data_file = "D:\Python\ML\data\zhengqi_train.txt"
test_data_file =  "D:\Python\ML\data\/zhengqi_test.txt"
train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')
#%%查看训练集特征变量信息
train_infor=train_data.describe()
test_infor=test_data.describe()

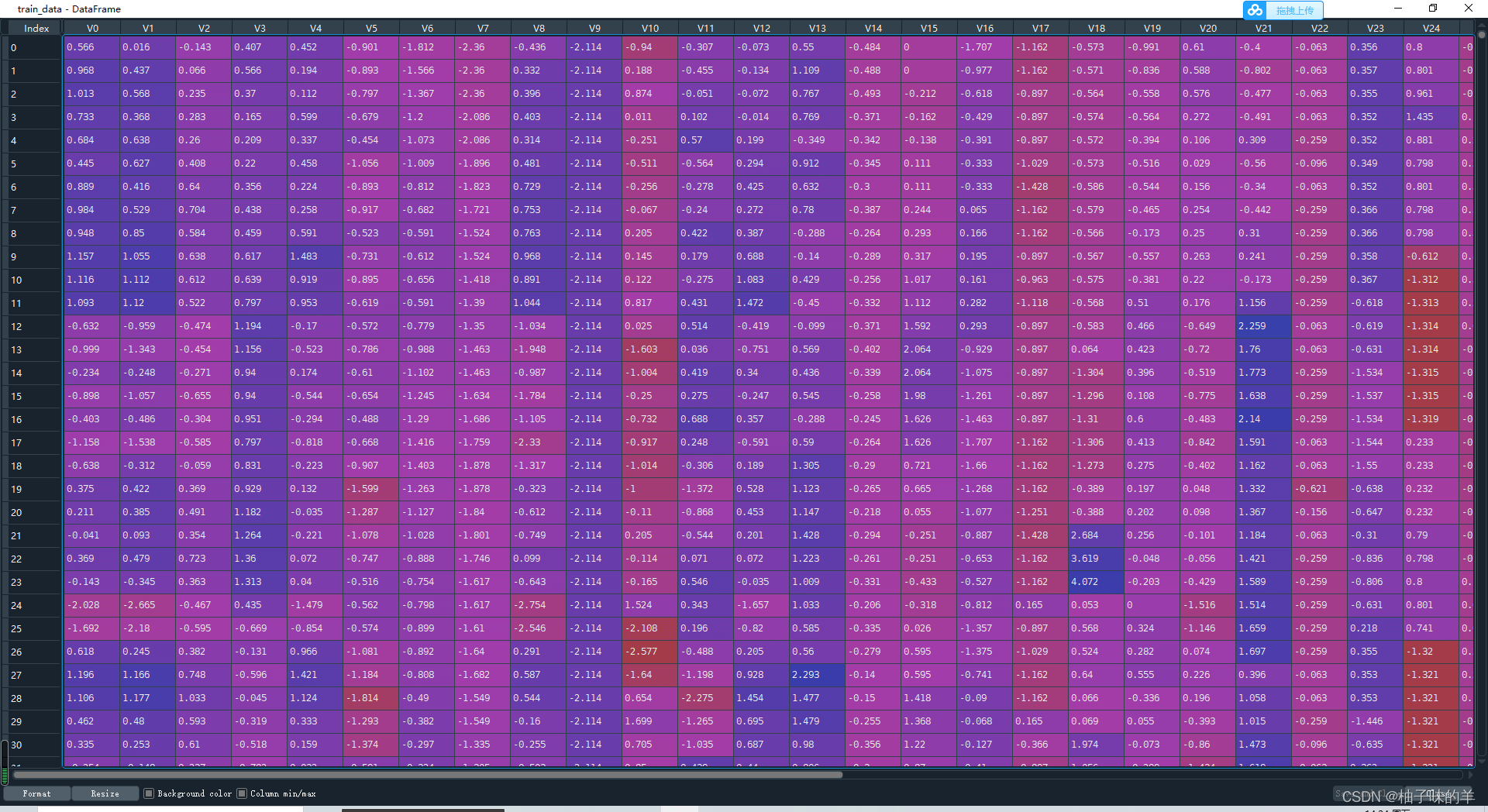
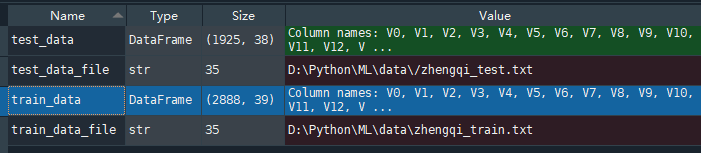
2 数据特征探索（数据可视化）

#%%可视化探索数据
# 画v0箱式图
fig = plt.figure(figsize=(4, 6))  # 指定绘图对象宽度和高度
sns.boxplot(y=train_data['V0'],orient="v", width=0.5)
#%%可以将所有的特征都画出
'''
column = train_data.columns.tolist()[:39]  # 列表头
fig = plt.figure(figsize=(20, 40))  # 指定绘图对象宽度和高度
for i in range(38):
    plt.subplot(13, 3, i + 1)  # 13行3列子图
    sns.boxplot(train_data[column[i]], orient="v", width=0.5)  # 箱式图
    plt.ylabel(column[i], fontsize=8)
plt.show()
'''
#%%查看v0的数据分布直方图，绘制QQ图查看数据是否近似于正态分布
plt.figure(figsize=(10,5))
ax=plt.subplot(1,2,1)
sns.distplot(train_data['V0'],fit=stats.norm)
ax=plt.subplot(1,2,2)
res = stats.probplot(train_data['V0'], plot=plt)
#%%查看所有特征的数据分布情况
'''
train_cols = 6
train_rows = len(train_data.columns)
plt.figure(figsize=(4*train_cols,4*train_rows))

i=0
for col in train_data.columns:
    i+=1
    ax=plt.subplot(train_rows,train_cols,i)
    sns.distplot(train_data[col],fit=stats.norm)

    i+=1
    ax=plt.subplot(train_rows,train_cols,i)
    res = stats.probplot(train_data[col], plot=plt)
plt.show()
'''

#%%对比统一特征训练集和测试集的分布情况，查看数据分布是否一致
ax = sns.kdeplot(train_data['V0'], color="Red", shade=True)
ax = sns.kdeplot(test_data['V0'], color="Blue", shade=True)
ax.set_xlabel('V0')
ax.set_ylabel("Frequency")
ax = ax.legend(["train","test"])

#%%查看所有特征的训练集和测试集分布情况
'''
dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4*dist_cols,4*dist_rows))

i=1
for col in test_data.columns:
    ax=plt.subplot(dist_rows,dist_cols,i)
    ax = sns.kdeplot(train_data[col], color="Red", shade=True)
    ax = sns.kdeplot(test_data[col], color="Blue", shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train","test"])

    i+=1
plt.show()
'''

#%%查看v5,v9,v11,v22,v28的数据分布
drop_col = 6
drop_row = 1

plt.figure(figsize=(5*drop_col,5*drop_row))
i=1
for col in ["V5","V9","V11","V17","V22","V28"]:
    ax =plt.subplot(drop_row,drop_col,i)
    ax = sns.kdeplot(train_data[col], color="Red", shade=True)
    ax = sns.kdeplot(test_data[col], color="Blue", shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train","test"])

    i+=1
plt.show()
#%%删除这些特征
drop_columns=["V5","V9","V11","V17","V22","V28"]
train_data=train_data.drop(columns=drop_columns)
test_data=test_data.drop(columns=drop_columns)

当训练数据和测试数据分布不一致的时候，会导致模型的泛化能力差，采用删除此类特征的方法

#%%可视化线性回归关系
fcols = 2
frows = 1
plt.figure(figsize=(8,4))
ax=plt.subplot(1,2,1)
sns.regplot(x='V0', y='target', data=train_data, ax=ax,
            scatter_kws={'marker':'.','s':3,'alpha':0.3},
            line_kws={'color':'k'});
plt.xlabel('V0')
plt.ylabel('target')

ax=plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')

plt.show()
#%%查看所有特征变量与target变量的线性回归关系
'''
fcols = 6
frows = len(test_data.columns)
plt.figure(figsize=(5*fcols,4*frows))

i=0
for col in test_data.columns:
    i+=1
    ax=plt.subplot(frows,fcols,i)
    sns.regplot(x=col, y='target', data=train_data, ax=ax,
                scatter_kws={'marker':'.','s':3,'alpha':0.3},
                line_kws={'color':'k'});
    plt.xlabel(col)
    plt.ylabel('target')

    i+=1
    ax=plt.subplot(frows,fcols,i)
    sns.distplot(train_data[col].dropna())
    plt.xlabel(col)
'''

#%%查看特征变量的相关性
train_corr = train_data.corr()
# 画出相关性热力图
ax = plt.subplots(figsize=(20, 16))#调整画布大小
ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True)#画热力图   annot=True 显示系数

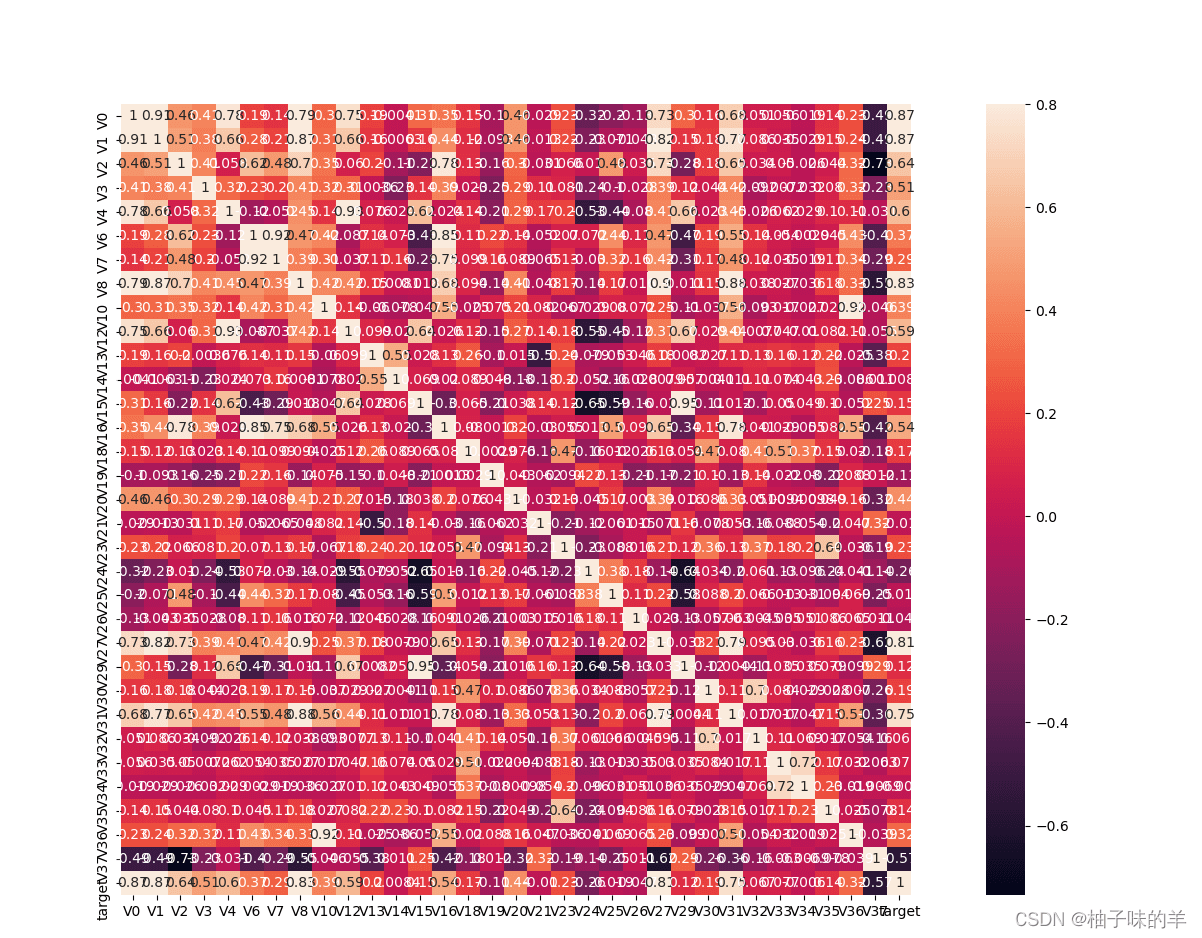
#%%找出相关程度
plt.figure(figsize=(20, 16))  # 指定绘图对象宽度和高度
colnm = train_data.columns.tolist()  # 列表头
mcorr = train_data[colnm].corr(method="spearman")  # 相关系数矩阵，即给出了任意两个变量之间的相关系数
mask = np.zeros_like(mcorr, dtype=np.bool)  # 构造与mcorr同维数矩阵 为bool型
mask[np.triu_indices_from(mask)] = True  # 角分线右侧为True
cmap = sns.diverging_palette(220, 10, as_cmap=True)  # 返回matplotlib colormap对象
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')  # 热力图（看两两相似度）
plt.show()

#%%查找特征变量和target变量相关系数大于0.5的特征变量
#寻找K个最相关的特征信息
k = 10 # number of variables for heatmap
cols = train_corr.nlargest(k, 'target')['target'].index

cm = np.corrcoef(train_data[cols].values.T)
hm = plt.subplots(figsize=(10, 10))#调整画布大小
hm = sns.heatmap(train_data[cols].corr(),annot=True,square=True)
plt.show()

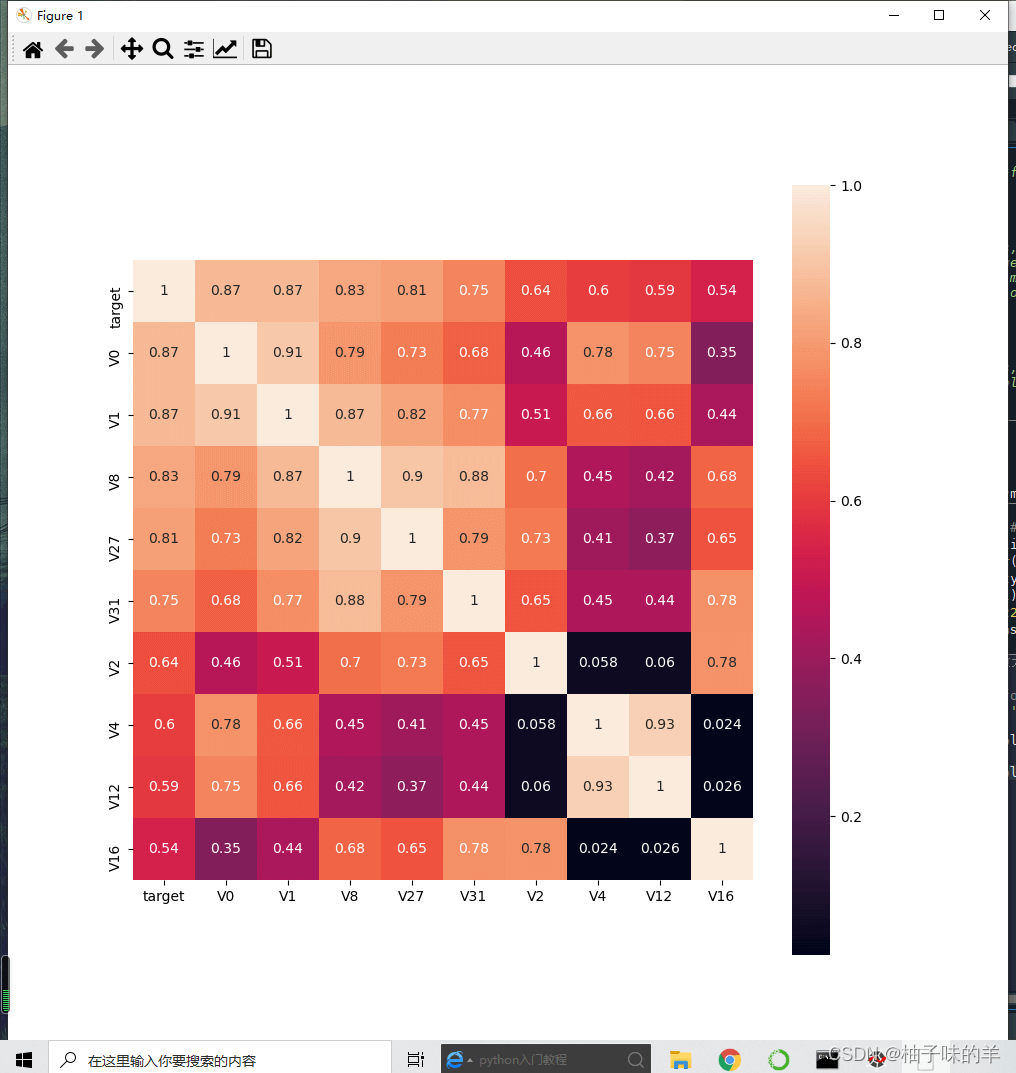
threshold = 0.5
corrmat = train_data.corr()
top_corr_features = corrmat.index[abs(corrmat["target"])>threshold]
plt.figure(figsize=(10,10))
g = sns.heatmap(train_data[top_corr_features].corr(),annot=True,cmap="RdYlGn")

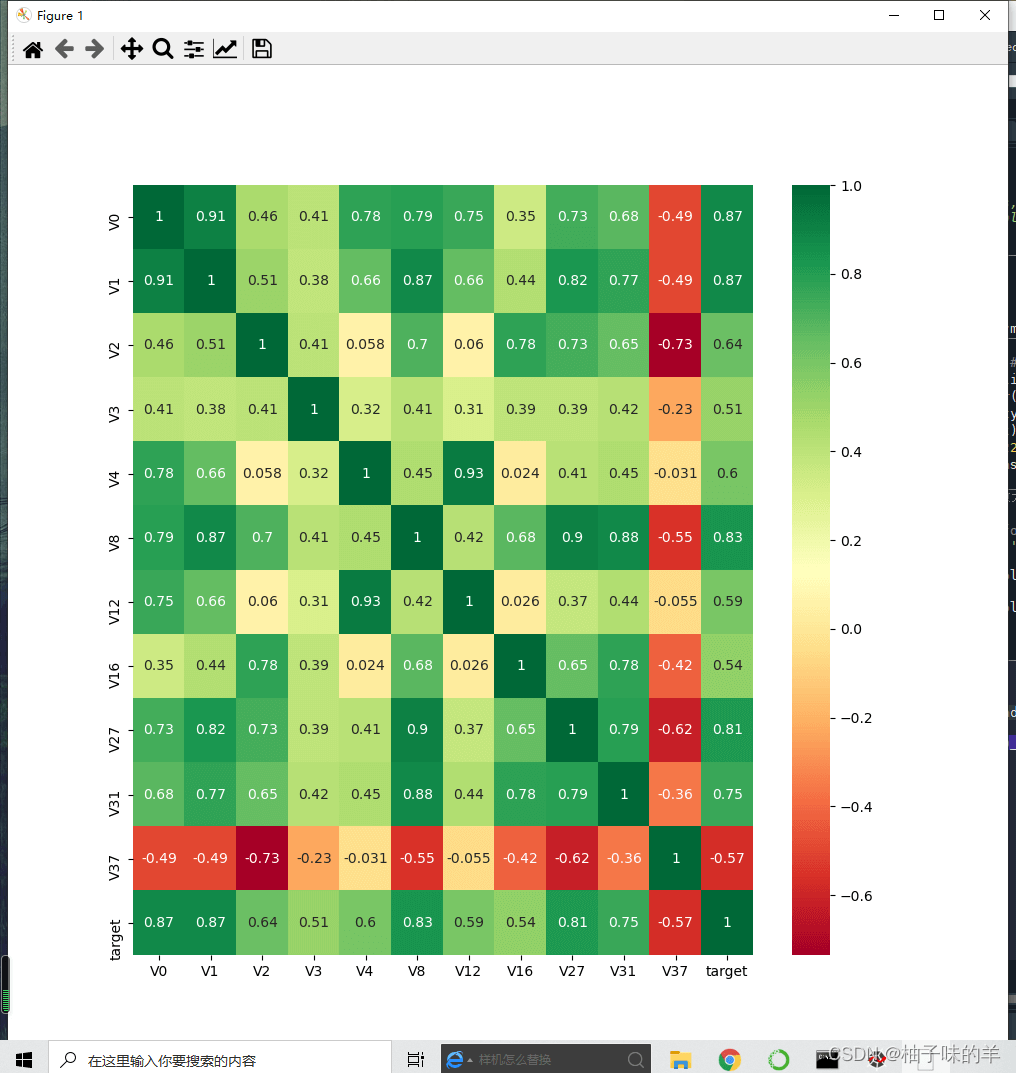
#%% Threshold for removing correlated variables
threshold = 0.05

# Absolute value correlation matrix
corr_matrix = train_data.corr().abs()
drop_col=corr_matrix[corr_matrix["target"]<threshold].index
#%%删除相关性小于0.05的列
train_data=train_data.drop(columns=drop_col)
test_data=test_data.drop(columns=drop_col)

#%%将train和test合并
train_x=train_data.drop(['target'],axis=1)
data_all=pd.concat([train_x,test_data])

#%%标准化
cols_numeric=list(data_all.columns)

def scale_minmax(col):
    return (col-col.min())/(col.max()-col.min())

data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax,axis=0)
print(data_all[cols_numeric].describe())
train_data_process = train_data[cols_numeric]
train_data_process = train_data_process[cols_numeric].apply(scale_minmax,axis=0)

test_data_process = test_data[cols_numeric]
test_data_process = test_data_process[cols_numeric].apply(scale_minmax,axis=0)

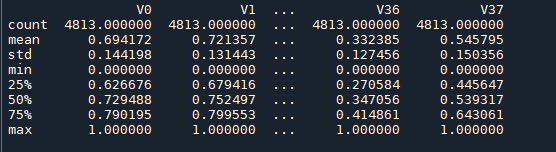
#%%查看v0-v3四个特征的箱盒图，查看其分布是否符合正态分布
cols_numeric_0to4 = cols_numeric[0:4]
## Check effect of Box-Cox transforms on distributions of continuous variables

train_data_process = pd.concat([train_data_process, train_data['target']], axis=1)

fcols = 6
frows = len(cols_numeric_0to4)
plt.figure(figsize=(4*fcols,4*frows))
i=0

for var in cols_numeric_0to4:
    dat = train_data_process[[var, 'target']].dropna()

    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(dat[var] , fit=stats.norm);
    plt.title(var+' Original')
    plt.xlabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(dat[var], plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
    plt.xlabel('')
    plt.ylabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(dat[var], dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))

    i+=1
    plt.subplot(frows,fcols,i)
    trans_var, lambda_var = stats.boxcox(dat[var].dropna()+1)
    trans_var = scale_minmax(trans_var)
    sns.distplot(trans_var , fit=stats.norm);
    plt.title(var+' Tramsformed')
    plt.xlabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(trans_var, plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var)))
    plt.xlabel('')
    plt.ylabel('')

    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(trans_var, dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))

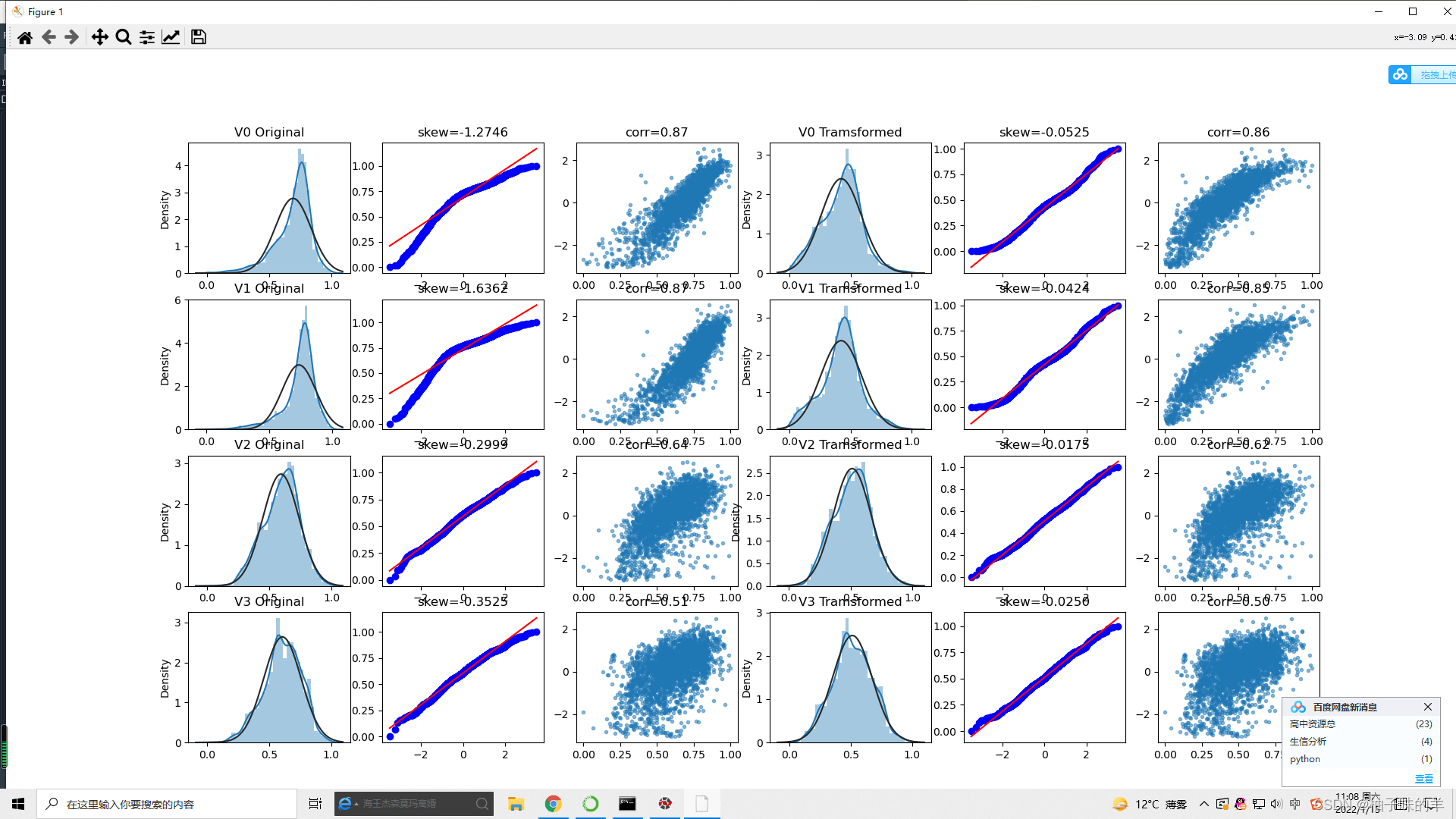
三、特征优化

import pandas as pd

train_data_file =  "D:\Python\ML\data\zhengqi_train.txt"
test_data_file =   "D:\Python\ML\data\zhengqi_test.txt"

train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')

#%%定义特征构造方法，构造特征
epsilon=1e-5

#组交叉特征，可以自行定义，如增加： x*x/y, log(x)/y 等等，使用lambda函数更方便快捷
func_dict = {
            'add': lambda x,y: x+y,
            'mins': lambda x,y: x-y,
            'div': lambda x,y: x/(y+epsilon),
            'multi': lambda x,y: x*y
            }
#%%定义特征构造函数
def auto_features_make(train_data,test_data,func_dict,col_list):
    train_data, test_data = train_data.copy(), test_data.copy()
    for col_i in col_list:
        for col_j in col_list:
            for func_name, func in func_dict.items():
                for data in [train_data,test_data]:
                    func_features = func(data[col_i],data[col_j])
                    col_func_features = '-'.join([col_i,func_name,col_j])
                    data[col_func_features] = func_features
    return train_data,test_data
#%%对训练集和测试集进行特征构造
train_data2, test_data2 = auto_features_make(train_data,test_data,func_dict,col_list=test_data.columns)

四、对特征构造后的训练集和测试集进行主成分分析

#%%PCA
from sklearn.decomposition import PCA   #主成分分析法

#PCA方法降维
pca = PCA(n_components=500)
train_data2_pca = pca.fit_transform(train_data2.iloc[:,0:-1])
test_data2_pca = pca.transform(test_data2)
train_data2_pca = pd.DataFrame(train_data2_pca)
test_data2_pca = pd.DataFrame(test_data2_pca)
train_data2_pca['target'] = train_data2['target']
X_train2 = train_data2[test_data2.columns].values
y_train = train_data2['target']

五、使用ＬｉｇｈｔＧＢＭ模型进行训练和预测

#%%使用lightgbm模型对新构造的特征进行模型训练和评估
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
import lightgbm as lgb
import numpy as np

# 5折交叉验证
kf = KFold(len(X_train2), shuffle=True, random_state=2019)
#%%
# 记录训练和预测MSE
MSE_DICT = {
    'train_mse':[],
    'test_mse':[]
}

# 线下训练预测
for i, (train_index, test_index) in enumerate(kf.split(X_train2)):
    # lgb树模型
    lgb_reg = lgb.LGBMRegressor(
        learning_rate=0.01,
        max_depth=-1,
        n_estimators=5000,
        boosting_type='gbdt',
        random_state=2019,
        objective='regression',
    )

    # 切分训练集和预测集
    X_train_KFold, X_test_KFold = X_train2[train_index], X_train2[test_index]
    y_train_KFold, y_test_KFold = y_train[train_index], y_train[test_index]

    # 训练模型
    lgb_reg.fit(
            X=X_train_KFold,y=y_train_KFold,
            eval_set=[(X_train_KFold, y_train_KFold),(X_test_KFold, y_test_KFold)],
            eval_names=['Train','Test'],
            early_stopping_rounds=100,
            eval_metric='MSE',
            verbose=50
        )

    # 训练集预测 测试集预测
    y_train_KFold_predict = lgb_reg.predict(X_train_KFold,num_iteration=lgb_reg.best_iteration_)
    y_test_KFold_predict = lgb_reg.predict(X_test_KFold,num_iteration=lgb_reg.best_iteration_) 

    print('第{}折 训练和预测 训练MSE 预测MSE'.format(i))
    train_mse = mean_squared_error(y_train_KFold_predict, y_train_KFold)
    print('------\n', '训练MSE\n', train_mse, '\n------')
    test_mse = mean_squared_error(y_test_KFold_predict, y_test_KFold)
    print('------\n', '预测MSE\n', test_mse, '\n------\n')

    MSE_DICT['train_mse'].append(train_mse)
    MSE_DICT['test_mse'].append(test_mse)
print('------\n', '训练MSE\n', MSE_DICT['train_mse'], '\n', np.mean(MSE_DICT['train_mse']), '\n------')
print('------\n', '预测MSE\n', MSE_DICT['test_mse'], '\n', np.mean(MSE_DICT['test_mse']), '\n------')

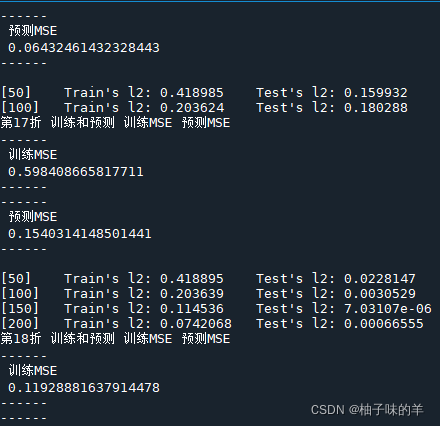
．．．．． 不想等它跑完了，会一直跑到ｓｃｏｒｅ不再变化或者ｒｏｕｎｄ＝１００的时候为止～

到此这篇关于Python机器学习应用之工业蒸汽数据分析篇详解的文章就介绍到这了,更多相关Python 工业蒸汽数据分析内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！