C++实现优先队列的示例详解

目录

• 前言
• 堆的存储方式
• 维护堆的方法
• 1、上浮操作
• 2、下沉操作
• 附上代码

前言

首先，啊，先简单介绍一下优先队列的概念，学数据结构以及出入算法竞赛的相信都对队列这一数据结构十分熟悉，这是一个线性的数据结构.

针对队列这一特殊数据结构，有时需考虑队列元素的优先级的关系，即根据用户自定义的优先级排序，出队时优先弹出优先级更高(低)的元素，优先队列能更好地满足实际问题中的需求，而在优先队列的各种实现中，堆是一种最高效的数据结构。

什么是堆

堆是一颗具有特定性质的二叉树，堆的基本要求就是堆中所有结点的值必须大于或等于（或小于或等于）其孩子结点的值，这也称为堆的性质，我们也叫堆序性；堆还有另一个性质，就是当 h > 0 时，所有叶子结点都处于第 h 或 h - 1 层（其中 h 为树的高度，完全二叉树），也就是说，堆应该是一颗完全二叉树；

如下:

根据两种堆序性，我们将堆分为两类，即根节点权值≥子节点权值的我们叫大根堆，根节点权值≤子节点权值的我们叫小根堆。道理简单，就不做图演示了。

上文所述，优先队列是由一个堆维护的，堆序性正对应了优先队列的优先级。由此，优先队列就并不是一个线性的数据结构，其所有操作都是logn的时间复杂度。

了解完堆与优先队列的关系，我们就可以开始讨论如何实现优先对列了。

堆的存储方式

我们将一个堆从上到下从左到右(实际上这个顺序也是堆一般的讨论模式)，从0开始给每个节点编号。如下图:

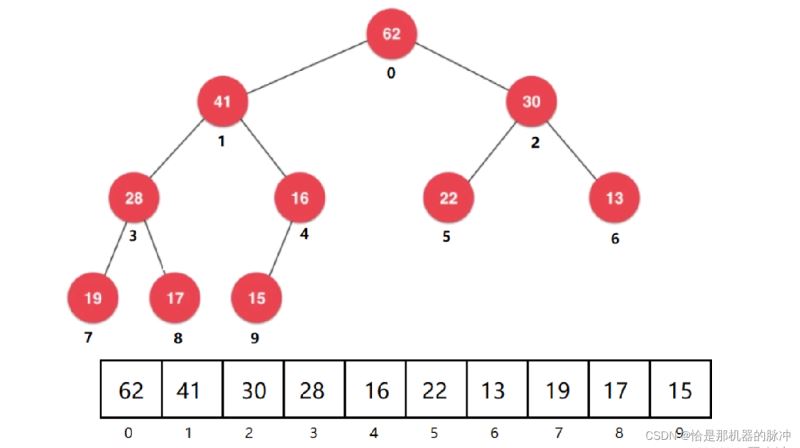
然后按照顺序存储进一个线性的数组之中，那么这就算存储好了~

简不简单？意不意外？是不是最开始想到的是递归生成树？但实际上因为堆序性的存在，我们并不需要那么复杂的存储方式~

同样的道理，我们反过来用一个数组建堆，也就是如上操作的逆操作而已。

问题就来了，如何用一个无序的数组来建堆呢？这就要谈到维护堆序性的两种操作——上浮，下沉。

维护堆的方法

1、上浮操作

首先将一个无序的数组按下标标号，然后开始进行前方所说的建堆操作，我们建堆的过程便是主要用到上浮操作，每操作一步就要与父节点比较，如果大于（此处以大根堆为例子）父节点，则与父节点进行交换，然后跳转到交换后的位置，继续与父节点进行比较，直到不大于父节点后，就算完成了一次调整。光说肯定有些童鞋无法想象得那么明白，下面放图！

这里用数组a[6] = {3,5,8,9,1,2}做模板，别多想，很随机的数字罢了。

第一步，将下标为0的节点做根节点，就是3啦~

第二步，将下标为1的节点也就是5作为3的左孩子~

很明显啊，5要比它的父节点3要大，那么，交换位置~

再看5并没有比它小的根节点了，那么继续下一步~

第三步，将下标为2的节点也就是8，放在5的下边作为右孩子~

很明显哦，8比它的父节点大，那么~，交换位置~

很明显，8并没有比它更小的父节点了，那么继续下一步~

再接下去我就不讲了，很简单，序号从上到下从左到右。

那么任一的一个节点如果它足够大（小），就一定会最底下一层爬到最大的根节点，是不是上浮呢，生动而形象，在建堆的时候每插入一个元素，就要对该元素进行一次上浮调整，将其放在正确的地方。 

相信聪明的童鞋已经发现了，同层的节点不存在任何的关系！！！甚至不同根节点的同层节点也不存在任何关系，每一个节点仅仅只是在其子堆中的最大值，即局部最大值。

2、下沉操作

该操作在队列的基本操作，也就是弹出队顶操作时所用，即删除最大（小）根节点的操作。

原理也很简单，将编号为0的节点与编号最大的节点权值互换，然后弹出编号最大的节点（此时即前一步的队顶元素），此时再对队顶节点进行下沉操作:

先与左子树进行比较，按照堆序性交换，直到换回它应在的位置，此时所有局部均为优先队列，其也维护完成。

上图:

这里还是前面那个数组，顺便也给大家看看建堆后的亚子~

a[6] = {3,5,8,9,1,2}

第一步， 将编号为0的节点与编号最大的节点权值互换

即将9与2进行互换。

第二步， 弹出编号最大的节点（此时即前一步的队顶元素）

即9

第三步， 对队顶节点进行下沉操作

即先和8，5进行顺序比较，按照优先级，明显与8互换，换完后如下

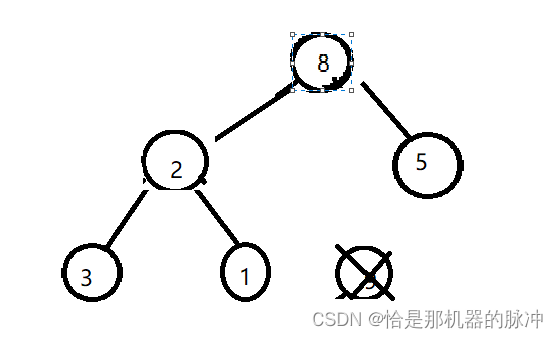
再与3先比较，无法交换再与1比较~最后应该是这个样子的。

两种操作方式也已经说完，这里就会有童鞋问道，那么如何在数组中进行所谓的上浮下沉，操作呢？ 

这里就有一个很重要的知识了，就是父节点和子节点在数组编号中的关系！

其实也并不难发现，根据堆的性质，有如下的关系：

设某个节点编号为i：

其父节点:dad = (i - 1) / 2

左/右子节点:left = 2 * i + 1

right = 2 * i + 2

这样大家就可以将上浮、下沉操作的每一步在数组中实现了！

附上代码

#include<iostream>
#include<cmath>
#include<stdlib.h>
#define bug cout<<"nug is here"<<endl;
#include<vector>
using namespace std;
typedef size_t ull;

//堆
template<typename P>
class Heap{
	private:
		vector<int> heap_elem;//堆容器
		ull heap_depth;//深度
		bool Priority; //优先级
		ull heap_size; //容量

		void Up_adjust(int now);//上浮调整
		void Down_adjust(int now);//下沉调整
		//now指代下标
	public:
		//构造堆
		enum{max_heap = true, min_heap = false};
		Heap(vector<P> &l, bool priority = max_heap){
			heap_size = l.size();
			heap_depth = log2(heap_size);
			Priority = priority;//设置优先级
			for(int i = 0;i < heap_size;i++){
				heap_elem.push_back(l[i]);
				Up_adjust(i);//上浮调整
			}
		}
		Heap(int a[], ull n, bool priority = max_heap){
			heap_size = n;
			heap_depth = log2(heap_size);
			Priority = priority;//设置优先级
			for(int i = 0;i < n;i++){
				heap_elem.push_back(a[i]);
				Up_adjust(i);//上浮调整
			}
		}
		Heap(){
			heap_size = 0;
			heap_depth = 0;
			Priority = max_heap;
		};

		//堆的成员函数
		ull Depth(){
			return heap_depth;
		}
		ull Size(){
			return heap_size;
		}
		void Push(P x){
			heap_elem.push_back(x);
			++heap_size;
			heap_depth = log2(heap_size);
			swap(heap_elem[heap_elem.size() - 1], heap_elem[heap_size - 1]);//将加入的元素放入有效位
			Up_adjust(heap_size - 1);
		}
		void Pop(){
			heap_depth = log2(heap_size);
			swap(heap_elem[--heap_size], heap_elem[0]);//将第一个元素与最后一个元素交换，并且缩短有效位数
			//其实这里可以用vector的函数pop_back（）,相应的上面的Push函数也不用换位置，但是这样更快
			Down_adjust(0);
		}
		P &Top(){
			return heap_elem[0];
		}
		void show_as_tree(){//以树的形式输出
			int _size = max(log10(heap_elem[0]),log10(heap_elem[heap_size - 1])) + 1;
			ull max_size = (pow(2, heap_depth) * 2) * _size;
			ull _max_size = _size * pow(2, heap_depth + 1);
			int start = -1;
			for(int i = 0;i <= heap_depth;i++){
				max_size >>= 1;
				max_size++;
				if(i == heap_depth) cout<<heap_elem[++start];
				else printf("%*d",max_size,heap_elem[++start]);
				int w = pow(2, i);
				for(int j = 1;j < w && start < heap_size - 1;j++) printf("%*d",_max_size,heap_elem[++start]);
				_max_size >>= 1;
				_max_size++;
				printf("\n");

			}

		}

		void show_as_array(){//数组方式输出
				for(int i = 0;i < heap_size;i++) cout<<heap_elem[i]<<" ";
				cout<<endl;
		}
};

//上浮调整
template<typename P>
void Heap<P>::Up_adjust(int now){
	if(Priority)
		while(now > 0 && heap_elem[now] > heap_elem[(now - 1) / 2]){//如果当前节点的权值比父亲大
			swap(heap_elem[now], heap_elem[(now - 1) / 2]);//交换
			now =  (now - 1) / 2;
		}
	else
		while(now > 0 && heap_elem[now] < heap_elem[(now - 1) / 2]){
			swap(heap_elem[now], heap_elem[(now - 1) / 2]);
			now = (now - 1) / 2;
		}
}

//下沉调整
template<typename P>
void Heap<P>::Down_adjust(int now){
	ull left = now * 2 + 1;
	ull right;
	while(left < heap_size){//能换的时候
		left = now * 2 + 1;
		right = now * 2 + 2;
		if(Priority){
			if(heap_elem[now] < heap_elem[left]){//比左孩子小，下沉
				swap(heap_elem[now], heap_elem[left]);
				now = left;
			}
			else if(right < heap_size){//比右孩子小，下沉
				if(heap_elem[now] > heap_elem[right]){
					swap(heap_elem[now], heap_elem[right]);
					now = right;
				}

			}
		}
		else{
			if(heap_elem[now] > heap_elem[left]){//比左孩子大，下沉
				swap(heap_elem[now], heap_elem[left]);
				now = left;
			}
			else if(right > heap_size){//比右孩子大，下沉
				if(heap_elem[now] < heap_elem[right]){
					swap(heap_elem[now], heap_elem[right]);
					now = right;
				}
			}
		}
	}
}

int main(){
	int a[6] = {3,5,8,9,1,2};
	Heap<int> h(a, 6, true);
	//输出堆
	h.show_as_tree();

//	h.Push(12);
//	h.show_as_tree();
//
//	h.Pop();
//	h.show_as_tree();
//
//	cout<<h.Top()<<endl;

//	vector<int> a;
//	Heap<int> h(a, Heap<int>::max_heap);
//	for(int i=0;i < 10;++i)
//		h.Push(rand()%100);
//
//	h.show_as_tree();
	return 0;
}

按照前面那个数组运行，结果如下:

是不是很神奇呢？

以上就是C++实现优先队列的示例详解的详细内容，更多关于C++优先队列的资料请关注我们其它相关文章！