C++实现softmax函数的面试经验

目录
  • 背景
  • 第一次实现
    • 实现
    • 测试
      • test 1
      • test 2
  • 第二次实现(改进)
    • 改进原理
    • 实现
    • 测试
      • test 1
      • test 2
  • 完整代码

背景

今天面试字节算法岗时被问到的问题，让我用C++实现一个softmax函数。softmax是逻辑回归在多分类问题上的推广。大概的公式如下：

即判断该变量在总体变量中的占比。

第一次实现

实现

我们用vector来封装输入和输出，简单的按公式复现。

vector<double> softmax(vector<double> input)
{
	double total=0;
	for(auto x:input)
	{
		total+=exp(x);
	}
	vector<double> result;
	for(auto x:input)
	{
		result.push_back(exp(x)/total);
	}
	return result;
}

测试

test 1

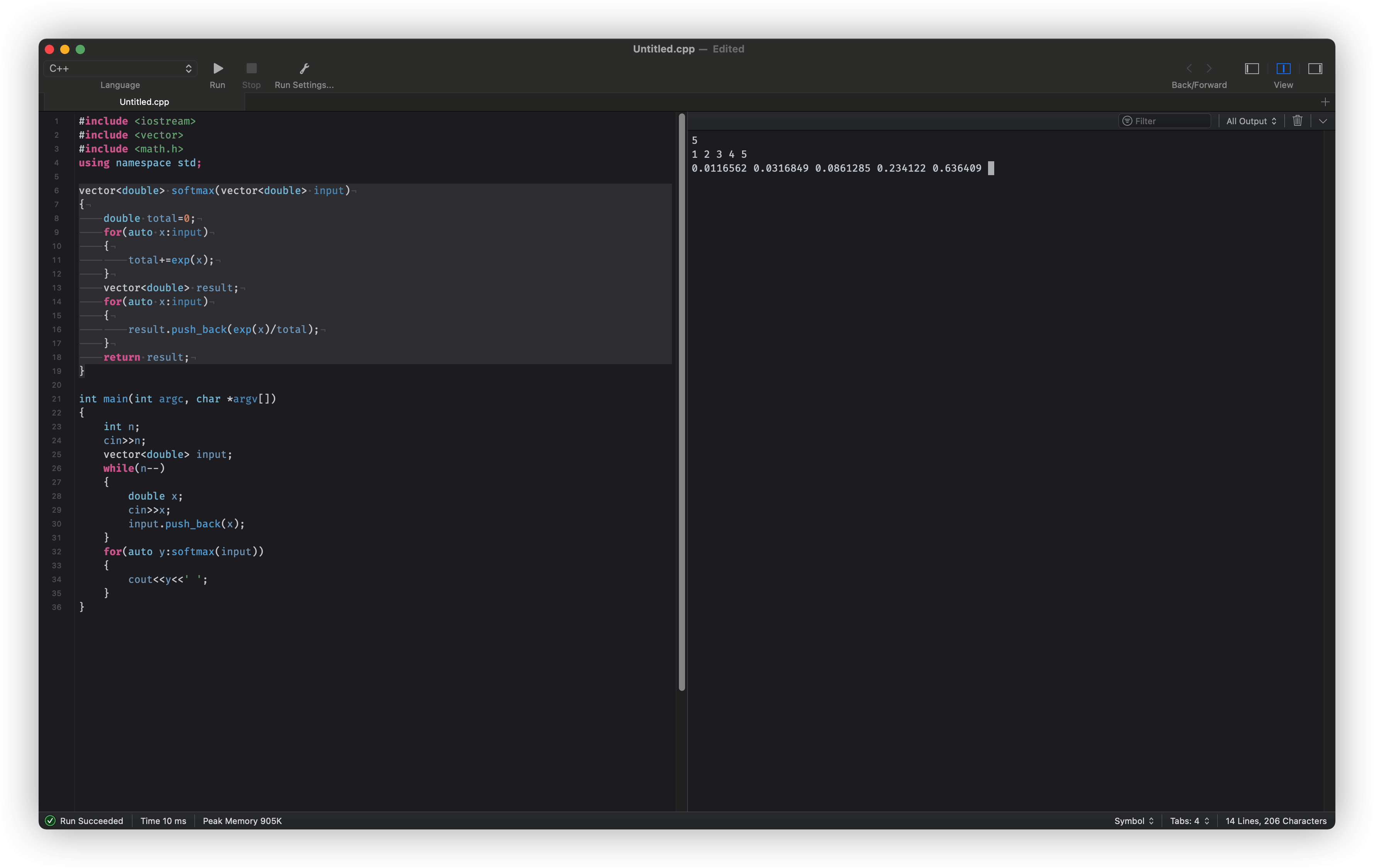
  • 测试用例1: {1, 2, 3, 4, 5}
  • 测试输出1: {0.0116562, 0.0316849, 0.0861285, 0.234122, 0.636409}

经过简单测试是正常的。

test 2

但是这时面试官提出了一个问题，即如果有较大输入变量时会怎么样？

  • 测试用例2: {1, 2, 3, 4, 5, 1000}
  • 测试输出2: {0, 0, 0, 0, 0, nan}

由于 e^1000已经溢出了双精度浮点(double)所能表示的范围，所以变成了NaN(not a number)。

第二次实现(改进)

改进原理

我们注意观察softmax的公式:

如果我们给上下同时乘以一个很小的数，最后答案的值是不变的。

那我们可以给每一个输入 x i 都减去一个值 a ，防止爆精度。

大致表示如下:

实现

vector<double> softmax(vector<double> input)
{
	double total=0;
	double MAX=input[0];
	for(auto x:input)
	{
		MAX=max(x,MAX);
	}
	for(auto x:input)
	{
		total+=exp(x-MAX);
	}
	vector<double> result;
	for(auto x:input)
	{
		result.push_back(exp(x-MAX)/total);
	}
	return result;
}

测试

test 1

  • 测试用例1: {1, 2, 3, 4, 5, 1000}
  • 测试输出1: {0, 0, 0, 0, 0, 1}

test 2

  • 测试用例1: {0, 19260817, 19260817}
  • 测试输出1: {0, 0.5, 0.5}

我们发现结果正常了。

完整代码

#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
vector<double> softmax(vector<double> input)
{
	double total=0;
	double MAX=input[0];
	for(auto x:input)
	{
		MAX=max(x,MAX);
	}
	for(auto x:input)
	{
		total+=exp(x-MAX);
	}
	vector<double> result;
	for(auto x:input)
	{
		result.push_back(exp(x-MAX)/total);
	}
	return result;
}
int main(int argc, char *argv[])
{
	int n;
	cin>>n;
	vector<double> input;
	while(n--)
	{
		double x;
		cin>>x;
		input.push_back(x);
	}
	for(auto y:softmax(input))
	{
		cout<<y<<' ';
	}
}

以上就是C++实现softmax函数的面试经验的详细内容，更多关于C++ softmax函数的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • TensorFlow实现Softmax回归模型

    一.概述及完整代码 对MNIST(MixedNational Institute of Standard and Technology database)这个非常简单的机器视觉数据集,Tensorflow为我们进行了方便的封装,可以直接加载MNIST数据成我们期望的格式.本程序使用Softmax Regression训练手写数字识别的分类模型. 先看完整代码: import tensorflow as tf from tensorflow.examples.tutorials.mnist imp

  • Softmax函数原理及Python实现过程解析

    Softmax原理 Softmax函数用于将分类结果归一化,形成一个概率分布.作用类似于二分类中的Sigmoid函数. 对于一个k维向量z,我们想把这个结果转换为一个k个类别的概率分布p(z).softmax可以用于实现上述结果,具体计算公式为: 对于k维向量z来说,其中zi∈R,我们使用指数函数变换可以将元素的取值范围变换到(0,+∞),之后我们再所有元素求和将结果缩放到[0,1],形成概率分布. 常见的其他归一化方法,如max-min.z-score方法并不能保证各个元素为正,且和为1. S

  • 浅谈pytorch中torch.max和F.softmax函数的维度解释

    在利用torch.max函数和F.Ssoftmax函数时,对应该设置什么维度,总是有点懵,遂总结一下: 首先看看二维tensor的函数的例子: import torch import torch.nn.functional as F input = torch.randn(3,4) print(input) tensor([[-0.5526, -0.0194, 2.1469, -0.2567], [-0.3337, -0.9229, 0.0376, -0.0801], [ 1.4721, 0.1

  • Python下的Softmax回归函数的实现方法(推荐)

    Python下的Softmax回归函数的实现方法(推荐)

    Softmax回归函数是用于将分类结果归一化.但它不同于一般的按照比例归一化的方法,它通过对数变换来进行归一化,这样实现了较大的值在归一化过程中收益更多的情况. Softmax公式 Softmax实现方法1 import numpy as np def softmax(x): """Compute softmax values for each sets of scores in x.""" pass # TODO: Compute and re

  • C++实现softmax函数的面试经验

    C++实现softmax函数的面试经验

    目录 背景 第一次实现 实现 测试 test 1 test 2 第二次实现(改进) 改进原理 实现 测试 test 1 test 2 完整代码 背景 今天面试字节算法岗时被问到的问题,让我用C++实现一个softmax函数.softmax是逻辑回归在多分类问题上的推广.大概的公式如下: 即判断该变量在总体变量中的占比. 第一次实现 实现 我们用vector来封装输入和输出,简单的按公式复现. vector<double> softmax(vector<double> input)

  • python编写softmax函数、交叉熵函数实例

    python代码如下: import numpy as np # Write a function that takes as input a list of numbers, and returns # the list of values given by the softmax function. def softmax(L): pass expL = np.exp(L) sumExpL = sum(expL) result = [] for i in expL: result.appen

  • 关于tensorflow softmax函数用法解析

    如下所示: def softmax(logits, axis=None, name=None, dim=None): """Computes softmax activations. This function performs the equivalent of softmax = tf.exp(logits) / tf.reduce_sum(tf.exp(logits), axis) Args: logits: A non-empty `Tensor`. Must be

  • 一次围绕setTimeout的前端面试经验分享

    前言 前端这个近年的热门领域,搞事气氛特别强烈,我朋友小伟最近就在疯狂面试,遇到了许多有趣的面试官,有趣的面试题,我来帮这个搞事 boy 转述一下. 具体如下: 以下是我一个朋友的故事,真的不是我. for (var i = 0; i < 5; i++) { console.log(i); } "小伟,你说说这几行代码会输出什么?" 当面试官在 Sublime 打出这几行代码时,我竟有点蒙蔽.蛤?这不是最简单的一个循环吗?是不是有陷阱啊,我思索一下,这好像和我看的那个闭包的题很像

  • 常用ASP函数集【经验才是最重要的】

    <%@LANGUAGE="VBSCRIPT" CODEPAGE="936"%> <% StartTime=timer() '程序执行时间检测 '############################################################### '┌──VIBO───────────────────┐ '│             VIBO STUDIO 版权所有             │ '└─────────────

  • Pytorch中Softmax和LogSoftmax的使用详解

    一.函数解释 1.Softmax函数常用的用法是指定参数dim就可以: (1)dim=0:对每一列的所有元素进行softmax运算,并使得每一列所有元素和为1. (2)dim=1:对每一行的所有元素进行softmax运算,并使得每一行所有元素和为1. class Softmax(Module): r"""Applies the Softmax function to an n-dimensional input Tensor rescaling them so that th

  • Pytorch中Softmax与LogSigmoid的对比分析

    Pytorch中Softmax与LogSigmoid的对比分析

    Pytorch中Softmax与LogSigmoid的对比 torch.nn.Softmax 作用: 1.将Softmax函数应用于输入的n维Tensor,重新改变它们的规格,使n维输出张量的元素位于[0,1]范围内,并求和为1. 2.返回的Tensor与原Tensor大小相同,值在[0,1]之间. 3.不建议将其与NLLLoss一起使用,可以使用LogSoftmax代替之. 4.Softmax的公式: 参数: 维度,待使用softmax计算的维度. 例子: # 随机初始化一个tensor a

  • Pytorch中torch.nn.Softmax的dim参数用法说明

    Pytorch中torch.nn.Softmax的dim参数用法说明

    Pytorch中torch.nn.Softmax的dim参数使用含义 涉及到多维tensor时,对softmax的参数dim总是很迷,下面用一个例子说明 import torch.nn as nn m = nn.Softmax(dim=0) n = nn.Softmax(dim=1) k = nn.Softmax(dim=2) input = torch.randn(2, 2, 3) print(input) print(m(input)) print(n(input)) print(k(inp

随机推荐