Python算法思想集结深入理解动态规划

目录

• 1. 概述
• 什么是重叠子问题
• 动态规划与分治算法的区别
• 什么最优子结构
• 2. 流程
• 2.1 是否存在子问题
• 2.2 是否存在重叠子问题
• 怎么解决重叠子问题
• 2.3 状态转移
• 3.总结

1. 概述

动态规划算法应用非常之广泛。

对于算法学习者而言，不跨过动态规划这道门，不算真正了解算法。

初接触动态规划者，理解其思想精髓会存在一定的难度，本文将通过一个案例，抽丝剥茧般和大家聊聊动态规划。

动态规划算法有 3 个重要的概念：

• 重叠子问题。
• 最优子结构。
• 状态转移。

只有吃透这 3 个概念，才叫真正理解什么是动态规划。

什么是重叠子问题

动态规划和分治算法有一个相似之处。

将原问题分解成相似的子问题，在求解的过程中通过子问题的解求出原问题的解。

动态规划与分治算法的区别

• 分治算法的每一个子问题具有完全独立性，只会被计算一次。
• 二分查找是典型的分治算法实现，其子问题是把数列缩小后再二分查找，每一个子问题只会被计算一次。
• 动态规划经分解得到的子问题往往不是互相独立的，有些子问题会被重复计算多次，这便是重叠子问题。
• 同一个子问题被计算多次，完全是没有必要的，可以缓存已经计算过的子问题，再次需要子问题结果时只需要从缓存中获取便可。这便是动态规划中的典型操作，优化重叠子问题，通过空间换时间的优化手段提高性能。

重叠子问题并不是动态规划的专利，重叠子问题是一个很普见的现象。

什么最优子结构

最优子结构是动态规划的必要条件。因为动态规划只能应用于具有最优子结构的问题，在解决一个原始问题时，是否能套用动态规划算法，分析是否存在最优子结构是关键。

那么！到底什么是最优子结构？概念其实很简单，局部最优解能决定全局最优解。

如拔河比赛中。如果 A队中的每一名成员的力气都是每一个班上最大的，由他们组成的拔河队毫无疑问，一定是也是所有拔河队中实力最强的。

如果把求解哪一个团队的力量最大当成原始问题，则每一个人的力量是否最大就是子问题，则子问题的最优决定了原始问题的最优。

所以，动态规划多用于求最值的应用场景。

不是说有 3 个概念吗！

不急，先把状态转移这个概念放一放，稍后再解释。

2. 流程

下面以一个案例的解决过程描述使用动态规划的流程。

问题描述：小兔子的难题。

有一只小兔子站在一片三角形的胡萝卜地的入口，如下图所示，图中的数字表示每一个坑中胡萝卜的数量，小兔子每次只能跳到左下角或者右下角的坑中，请问小兔子怎么跳才能得到最多数量的胡萝卜？

首先这个问题是求最值问题， 是否能够使用动态规划求解，则需要一步一步分析，看是否有满足使用动态规划的条件。

2.1 是否存在子问题

先来一个分治思想：思考或观察是否能把原始问题分解成相似的子问题，把解决问题的希望寄托在子问题上。

那么，针对上述三角形数列，是否存在子问题？

现在从数字7出发，兔子有 2 条可行路线。

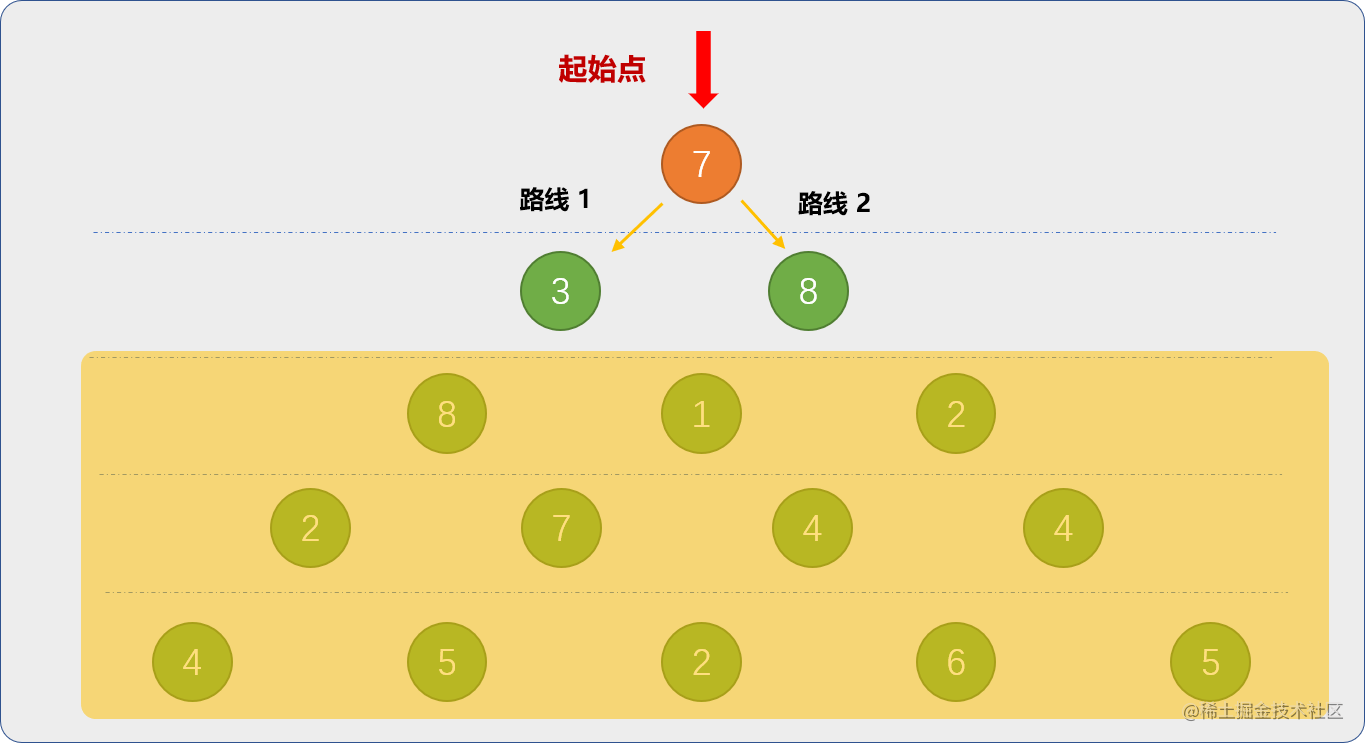
为了便于理解，首先模糊第 3 行后面的数字或假设第 3行之后根本不存在。

那么原始问题就变成：

• 先分别求解路线 1 和路线 2上的最大值。路线 1的最大值为 3,路线 2上的最大值是8。
• 然后求解出路线 1和路线 2两者之间的最大值 8。 把求得的结果和出发点的数字 7 相加，7+8=15 就是最后答案。
• 只有 2 行时，兔子能获得的最多萝卜数为 15，肉眼便能看的出来。

前面是假设第 3 行之后都不存在，现在把第 3 行放开，则路线 1 路线2的最大值就要发生变化，但是，对于原始问题来讲，可以不用关心路线 1 和路线 2 是怎么获取到最大值，交给子问题自己处理就可以了。

反正，到时从路线 1 和路线 2 的结果中再选择一个最大值就是。

把第 3 行放开后，路线 1 就要重新更新最大值，如上图所示，路线 1也可以分解成子问题，分解后，也只需要关心子问题的返回结果。

• 路线 1 的子问题有 2个，路线 1_1和路线1_2。求解 2 个子问题的最大值后，再在 2 个子问题中选择最大值8，最后路线 1的最大值为3+8=11。
• 路线 2 的子问题有 2个，路线 2_1和路线2_2。求解 2 个子问题的最大值后，再在 2 个子问题中选择最大值2，最后路线 2的最大值为8+2=10。

当第 3 行放开后，更新路线 1和路线2的最大值，对于原始问题而言，它只需要再在 2 个子问题中选择最大值 11，最终问题的解为7+11=18。

如果放开第 4 行，将重演上述的过程。和原始问题一样，都是从一个点出发，求解此点到目标行的最大值。所以说，此问题是存在子问题的。

并且，只要找到子问题的最优解，就能得到最终原始问题的最优解。不仅存在子问题，而且存在最优子结构。

显然，这很符合递归套路：递进给子问题，回溯子问题的结果。

• 使用二维数列表保存三角形数列中的所有数据。a=[[7],[3,8],[8,1,2],[2,7,4,4],[4,5,2,6,5]]。
• 原始问题为 f(0，0)从数列的(0,0)出发，向左下角和右下角前行，一直找到此路径上的数字相加为最大。
• f(0,0)表示以第 1 行的第 1 列数字为起始点。
• 分解原始问题 f(0,0)=a(0,0)+max(f(1,0)+f(1,1))。
• 因为每一个子问题又可以分解，让表达式更通用 f(i,j)=a(i,j)+max(f(i+1,j)+f(i+1,j+1))。
• (i+1,j)表示 (i,j)的左下角，(i+1,j+1)表示 (i,j)的右下角，

编码实现：

# 已经数列
nums = [[7], [3, 8], [8, 1, 2], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
# 递归函数
def get_max_lb(i, j):
    if i == len(nums) - 1:
        # 递归出口
        return nums[i][j]
    # 分解子问题
    return nums[i][j] + max(get_max_lb(i + 1, j), get_max_lb(i + 1, j + 1))
# 测试
res = get_max_lb(0, 0)
print(res)
'''
输出结果
30
'''

不是说要聊聊动态规划的流程吗！怎么跑到递归上去了。

其实所有能套用动态规划的算法题，都可以使用递归实现，因递归平时接触多，从递归切入，可能更容易理解。

2.2 是否存在重叠子问题

先做一个实验，增加三角形数的行数，也就是延长路径线。

import random
nums = []
# 递归函数
def get_max_lb(i, j):
    if i == len(nums) - 1:
        return nums[i][j]
    return nums[i][j] + max(get_max_lb(i + 1, j), get_max_lb(i + 1, j + 1))
# 构建 100 行的二维列表
for i in range(100):
    nums.append([])
    for j in range(i + 1):
        nums[i].append(random.randint(1, 100))
res = get_max_lb(0, 0)
print(res)

执行程序后，久久没有得到结果，甚至会超时。原因何在？如下图：

路线1_2和路线2_1的起点都是从同一个地方（蓝色标注的位置）出发。显然，从数字 1（蓝色标注的数字）出发的这条路径会被计算 2 次。在上图中被重复计算的子路径可不止一条。

**这便是重叠子问题！**子问题被重复计算。

当三角形数列的数据不是很多时，重复计算对整个程序的性能的影响微不足道 。如果数据很多时，大量的重复计算会让计算机性能低下，并可能导致最后崩溃。

因为使用递归的时间复杂度为O(2^n)。当数据的行数变多时，可想而知，性能有多低下。

怎么解决重叠子问题

答案是：使用缓存，把曾经计算过的子问题结果缓存起来，当再次需要子问题结果时，直接从缓存中获取，就没有必要再次计算。

这里使用字典作为缓存器，以子问题的起始位置为关键字，以子问题的结果为值。

import random
def get_max_lb(i, j):
    if i == len(nums) - 1:
        return nums[i][j]
    left_max = None
    right_max = None
    if (i + 1, j) in dic.keys():
        # 检查缓存中是否存在子问题的结果
        left_max = dic[i + 1, j]
    else:
        # 缓存中没有，才递归求解
        left_max = get_max_lb(i + 1, j)
        # 求解后的结果缓存起来
        dic[(i + 1, j)] = left_max
    if (i + 1, j + 1) in dic.keys():
        right_max = dic[i + 1, j + 1]
    else:
        right_max = get_max_lb(i + 1, j + 1)
        dic[(i + 1, j + 1)] = right_max
    return nums[i][j] + max(left_max, right_max)
# 已经数列
nums = []
# 缓存器
dic = {}
for i in range(100):
    nums.append([])
    for j in range(i + 1):
        nums[i].append(random.randint(1, 100))
# 递归调用
res = get_max_lb(0, 0)
print(res)

因使用随机数生成数据，每次运行结果不一样。但是，每次运行后的速度是非常给力的。

当出现重叠子问题时，可以缓存曾经计算过的子问题。

好 ！现在到了关键时刻，屏住呼吸，从分析缓存中的数据开始。

使用递归解决问题，从结构上可以看出是从上向下的一种处理机制。所谓从上向下，也就是由原始问题开始一路去寻找答案。从本题来讲，就是从第一行一直找到最后一行，或者说从未知找到``已知`。

根据递归的特点，可知缓存数据的操作是在回溯过程中发生的。

当再次需要调用某一个子问题时，这时才有可能从缓存中获取到已经计算出来的结果。缓存中的数据是每一个子问题的结果，如果知道了某一个子问题，就可以通过子问题计算出父问题。

这时，可能就会有一个想法？

从已知找到未知。

任何一条路径只有到达最后一行后才能知道最后的结果。可以认为，最后一行是已知数据。先缓存最后一行，那么倒数第 2 行每一个位置到最后一行的路径的最大值就可以直接求出来。

同理，知道了倒数第 2 行的每一个位置的路径最大值，就可以求解出倒数第 3行每一个位置上的最大值。以此类推一直到第 1 行。

天呀！多完美，还用什么递归。

可以认为这种思想便是动态规划的核心：自下向上。

2.3 状态转移

还差最后一步，就能把前面的递归转换成动态规划实现。

什么是状态转移？

前面分析从最后 1 开始求最大值过程，是不是有点像田径场上的多人接力赛跑，第 1 名运动力争跑第 1，把状态转移给第 2名运动员，第 2名运动员持续保持第 1，然后把状态转移给第 3运动员，第 3名运动员也保持他这一圈的第 1，一至到最后一名运动员，都保持自己所在那一圈中的第 1。很显然最后结果，他们这个团队一定是第 1名。

把子问题的值传递给另一个子问题，这便是状态转移。当然在转移过程中，一定会存在一个表达式，用来计算如何转移。

用来保存每一个子问题状态的表称为 dp 表，其实就是前面递归中的缓存器。

用来计算如何转移的表达式，称为状态转移方程式。

有了上述的这张表，就可以使用动态规划自下向上的方式解决“兔子的难题”这个问题。

nums = [[7], [3, 8], [8, 1, 2], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
# dp列表
dp = []
idx = 0
# 从最后一行开始
for i in range(len(nums) - 1, -1, -1):
    dp.append([])
    for j in range(len(nums[i])):
        if i == len(nums) - 1:
            # 最后一行缓存于状态转移表中
            dp[idx].append(nums[i][j])
        else:
            dp[idx].append(nums[i][j] + max(dp[idx - 1][j], dp[idx - 1][j + 1]))
    idx += 1
print(dp)
'''
输出结果：
[[4, 5, 2, 6, 5], [7, 12, 10, 10], [20, 13, 12], [23, 21], [30]]
'''

程序运行后，最终输出结果和前面手工绘制的dp表中的数据一模一样。

其实动态规划实现是前面递归操作的逆过程。时间复杂度是O(n^2)。

并不是所有的递归操作都可以使用动态规划进行逆操作，只有符合动态规划条件的递归操作才可以。

上述解决问题时，使用了一个二维列表充当dp表，并保存所有的中间信息。

思考一下，真的有必要保存所有的中间信息吗？

在状态转移过程中，我们仅关心当前得到的状态信息，曾经的状态信息其实完全可以不用保存。

所以，上述程序完全可以使用一个一维列表来存储状态信息。

nums = [[7], [3, 8], [8, 1, 2], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
# dp表
dp = []
# 临时表
tmp = []
# 从最后一行开始
for i in range(len(nums) - 1, -1, -1):
    # 把上一步得到的状态数据提出来
    tmp = dp.copy()
    # 清除 dp 表中原来的数据，准备保存最新的状态数据
    dp.clear()
    for j in range(len(nums[i])):
        if i == len(nums) - 1:
            # 最后一行缓存于状态转移表中
            dp.append(nums[i][j])
        else:
            dp.append(nums[i][j] + max(tmp[j], tmp[j + 1]))
print(dp)
'''
输出结果：
[30]
'''

3.总结

动态规划问题一般都可以使用递归实现，递归是一种自上向下的解决方案，而动态规划是自下向上的解决方案，两者在解决同一个问题时的思考角度不一样，但本质是一样的。

并不是所有的递归操作都能转换成动态规划，是否能使用动态规划算法，则需要原始问题符合最优子结构和重叠子问题这 2 个条件。在使用动态规划过程中，找到状态转移表达式是关键。

以上就是Python算法思想集结深入理解动态规划的详细内容，更多关于Python算法动态规划的资料请关注我们其它相关文章！