详解python算法之冒泡排序
python之冒泡排序
概念: 重复地走访过要排序的元素列，依次比较两个相邻的元素，如果他们的顺序（如从大到小、首字母从A到Z）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素已经排序完成
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。
算法原理
冒泡排序算法的原理如下：
比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
算法分析
时间复杂度
若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数
和记录移动次数
均达到最小值：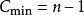
，
。
所以，冒泡排序最好的时间复杂度为
。
冒泡排序的最坏时间复杂度为
代码实现
伪代码
function bubble_sort (array, length) {
var i, j;
for(i from 1 to length-1){
for(j from 0 to length-1-i){
if (array[j] > array[j+1])
swap(array[j], array[j+1])
}
}
}
伪代码解释
函数 冒泡排序 输入 一个数组名称为array 其长度为length
i 从 1 到 (length - 1)
j 从 0 到 (length - 1 - i)
如果 array[j] > array[j + 1]
交换 array[j] 和 array[j + 1] 的值
如果结束
j循环结束
i循环结束
函数结束
助记码
i∈[0,N-1) //循环N-1遍 j∈[0,N-1-i) //每遍循环要处理的无序部分 swap(j,j+1) //两两排序（升序/降序）
python代码
#-*-coding:utf-8-*-
'''冒泡排序也称 bubble sort从小到大排序'''
import time
def bubble_sort(lst):
'''冒泡排序'''
# 第一次循环
for n in range(len(lst) - 1, 0, -1): #计算原列表的长度-1,取倒序索引
for i in range(n):
if lst[i] > lst[i + 1]: # 比较最后一个与倒数第二个数的值,如果倒数第二个的值,大于最后一个的值
temp = lst[i] # 则将倒数第二个值赋值给临时变量temp
lst[i] = lst[i + 1] # 替换原列表中倒数第二个索引的值为最后一个
lst[i + 1] = temp # 同时改变原列表中最后一个索引值为倒数第二个的值
return lst
if __name__ == "__main__":
lst = [54, 26, 93, 17, 77, 31, 44, 55, 20]
af_sort=bubble_sort(lst)
print(af_sort)
总结冒泡排序的实现（类似下面）通常会对已经排序好的数列拙劣地运行（
），而插入排序在这个例子只需要
个运算。算法的核心知识点是: 循环比较, 交叉换位!
相关推荐
-
详解Python3中的迭代器和生成器及其区别
介绍 本篇将介绍Python3中的迭代器与生成器,描述可迭代与迭代器关系,并实现自定义类的迭代器模式. 迭代的概念 上一次输出的结果为下一次输入的初始值,重复的过程称为迭代,每次重复即一次迭代,并且每次迭代的结果是下一次迭代的初始值 注:循环不是迭代 while True: #只满足重复,因而不是迭代 print('====>') 迭代器 1.为什么要有迭代器? 对于没有索引的数据类型,必须提供一种不依赖索引的迭代方式. 2.迭代器定义: 迭代器:可迭代对象执行__iter__方法,得到的结果
-
Python数据结构与算法之图的基本实现及迭代器实例详解
本文实例讲述了Python数据结构与算法之图的基本实现及迭代器.分享给大家供大家参考,具体如下: 这篇文章参考自<复杂性思考>一书的第二章,并给出这一章节里我的习题解答. (这书不到120页纸,要卖50块!!,一开始以为很厚的样子,拿回来一看,尼玛.....代码很少,给点提示,然后让读者自己思考怎么实现) 先定义顶点和边 class Vertex(object): def __init__(self, label=''): self.label = label def __repr__(sel
-
Python cookbook（数据结构与算法）从任意长度的可迭代对象中分解元素操作示例
本文实例讲述了python从任意长度的可迭代对象中分解元素操作.分享给大家供大家参考,具体如下: 从某个可迭代对象中分解出N个元素,但是可迭代对象的长度可能超过N,会出现"分解值过多"的异常: 使用"*表达式"来解决该问题: Python 3.4.3 (v3.4.3:9b73f1c3e601, Feb 24 2015, 22:43:06) [MSC v.1600 32 bit (Intel)] on win32 Type "copyright",
-
Python3爬楼梯算法示例
本文实例讲述了Python3爬楼梯算法.分享给大家供大家参考,具体如下: 假设你正在爬楼梯.需要 n 步你才能到达楼顶. 每次你可以爬 1 或 2 个台阶.你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数. 方案一:每一步都是前两步和前一步的和 class Solution(object): def climbStairs(self, n): """ :type n: int :rtype: int """ pre, cur =
-
Python生成一个迭代器的实操方法
Python怎么生成一个迭代器,对于需要处理大型数据来说,迭代器是必不可少的,这样可节省大量内存空间,更加合理操作数据. 首先我们打开编辑器,这里以Sublime text3作为示范,创建一个新的py文档. rg = range(100) for i in rg: print(i) 我们知道range可以涵盖比较广的范围,但是如果数据太大的时候,一次性打印会占用比较多内存. rg = range(100) rg_iter = iter(rg) print(rg_iter) 那么这个时候我们就可以
-
Gauss-Seidel迭代算法的Python实现详解
import numpy as np import time 1.1 Gauss-Seidel迭代算法 def GaussSeidel_tensor_V2(A,b,Delta,m,n,M): start=time.perf_counter() find=0 X=np.ones(n) d=np.ones(n) m1=m-1 m2=2-m for i in range(M): print('X',X) x=np.copy(X) #迭代更新 for j in range(n): a=np.copy(A
-
详解python算法之冒泡排序
python之冒泡排序 概念: 重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如从大到小.首字母从A到Z)错误就把他们交换过来.走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素已经排序完成 这个算法的名字由来是因为越大的元素会经由交换慢慢"浮"到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名"冒泡排序". 算法原理 冒泡排序算法的原理如下: 比较相邻的元素.如果第一个比第二个大,就交换他
-
详解python算法常用技巧与内置库
近些年随着python的越来越火,python也渐渐成为了很多程序员的喜爱.许多程序员已经开始使用python作为第一语言来刷题. 最近我在用python刷题的时候想去找点python的刷题常用库api和刷题技巧来看看.类似于C++的STL库文档一样,但是很可惜并没有找到,于是决定结合自己的刷题经验和上网搜索做一份文档出来,供自己和大家观看查阅. 1.输入输出: 1.1 第一行给定两个值n,m,用空格分割,第一个n决定接下来有n行的输入,m决定每一行有多少个数字,m个数字均用空格分隔. 解决办法
-
详解K-means算法在Python中的实现
K-means算法简介 K-means是机器学习中一个比较常用的算法,属于无监督学习算法,其常被用于数据的聚类,只需为它指定簇的数量即可自动将数据聚合到多类中,相同簇中的数据相似度较高,不同簇中数据相似度较低. K-MEANS算法是输入聚类个数k,以及包含 n个数据对象的数据库,输出满足方差最小标准k个聚类的一种算法.k-means 算法接受输入量 k :然后将n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高:而不同聚类中的对象相似度较小. 核心思想 通过迭代寻找
-
python实现连续变量最优分箱详解--CART算法
关于变量分箱主要分为两大类:有监督型和无监督型 对应的分箱方法: A. 无监督:(1) 等宽 (2) 等频 (3) 聚类 B. 有监督:(1) 卡方分箱法(ChiMerge) (2) ID3.C4.5.CART等单变量决策树算法 (3) 信用评分建模的IV最大化分箱 等 本篇使用python,基于CART算法对连续变量进行最优分箱 由于CART是决策树分类算法,所以相当于是单变量决策树分类. 简单介绍下理论: CART是二叉树,每次仅进行二元分类,对于连续性变量,方法是依次计算相邻两元素值的中位
-
详解python 支持向量机(SVM)算法
相比于逻辑回归,在很多情况下,SVM算法能够对数据计算从而产生更好的精度.而传统的SVM只能适用于二分类操作,不过却可以通过核技巧(核函数),使得SVM可以应用于多分类的任务中. 本篇文章只是介绍SVM的原理以及核技巧究竟是怎么一回事,最后会介绍sklearn svm各个参数作用和一个demo实战的内容,尽量通俗易懂.至于公式推导方面,网上关于这方面的文章太多了,这里就不多进行展开了~ 1.SVM简介 支持向量机,能在N维平面中,找到最明显得对数据进行分类的一个超平面!看下面这幅图: 如上图中,
-
详解KMP算法以及python如何实现
算法思路 Knuth-Morris-Pratt(KMP)算法是解决字符串匹配问题的经典算法,下面通过一个例子来演示一下: 给定字符串"BBC ABCDAB ABCDABCDABDE",检查里面是否包含另一个字符串"ABCDABD". 1.从头开始依次匹配字符,如果不匹配就跳到下一个字符 2.直到发现匹配字符,然后经过一个内循环严查字符串是否匹配 3.发现最后一个D不匹配,下面就该思考应该把字符串向右移动多少个位置呢?传统做法可能是移动一格,KMP算法就创新在这里.K
-
详解Bagging算法的原理及Python实现
目录 一.什么是集成学习 二.Bagging算法 三.Bagging用于分类 四.Bagging用于回归 一.什么是集成学习 集成学习是一种技术框架,它本身不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务,一般结构是:先产生一组"个体学习器",再用某种策略将它们结合起来,目前,有三种常见的集成学习框架(策略):bagging,boosting和stacking 也就是说,集成学习有两个主要的问题需要解决,第一是如何得到若干个个体学习器,第二是如何选择一种结合策
-
详解Python数据结构与算法中的顺序表
目录 0. 学习目标 1. 线性表的顺序存储结构 1.1 顺序表基本概念 1.2 顺序表的优缺点 1.3 动态顺序表 2. 顺序表的实现 2.1 顺序表的初始化 2.2 获取顺序表长度 2.3 读取指定位置元素 2.4 查找指定元素 2.5 在指定位置插入新元素 2.6 删除指定位置元素 2.7 其它一些有用的操作 3. 顺序表应用 3.1 顺序表应用示例 3.2 利用顺序表基本操作实现复杂操作 0. 学习目标 线性表在计算机中的表示可以采用多种方法,采用不同存储方法的线性表也有着不同的名称和特
-
详解Python结合Genetic Algorithm算法破解网易易盾拼图验证
首先看一下目标的验证形态是什么样子的 是一种通过验证推理的验证方式,用来防人机破解的确是很有效果,但是,But,这里面已经会有一些破绽,比如: (以上是原图和二值化之后的结果) (这是正常图片) 像划红线的这些地方,可以看到有明显的突变,并且二值化之后边缘趋于直线,但是正常图像是不会有这种这么明显的突变现象. 初识潘多拉 后来,我去翻阅了机器视觉的相关文章和论文,发现了一个牛逼的算法,这个算法就是——Genetic Algorithm遗传算法,最贴心的的是,作者利用这个算法实现了一个功能,“拼图
-
图文详解感知机算法原理及Python实现
目录 写在前面 1.什么是线性模型 2.感知机概述 3.手推感知机原理 4.Python实现 4.1 创建感知机类 4.2 更新权重与偏置 4.3 判断误分类点 4.4 训练感知机 4.5 动图可视化 5.总结 写在前面 机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用.“深”在详细推导算法模型背后的数学原理:“广”在分析多个机器学习模型:决策树.支持向量机.贝叶斯与马尔科夫决策.强化学习等. 本期目标:实现这样一个效果 1.什么是线性模型 线性模型的假设形式是属性权重.偏置与属性