floyd算法实现思路及实例代码

正如我们所知道的，Floyd算法用于求最短路径。Floyd算法可以说是Warshall算法的扩展，三个for循环就可以解决问题，所以它的时间复杂度为O(n^3)。

Floyd算法的基本思想如下：从任意节点A到任意节点B的最短路径不外乎2种可能，1是直接从A到B，2是从A经过若干个节点X到B。所以，我们假设Dis(AB)为节点A到节点B的最短路径的距离，对于每一个节点X，我们检查Dis(AX) + Dis(XB) < Dis(AB)是否成立，如果成立，证明从A到X再到B的路径比A直接到B的路径短，我们便设置Dis(AB) = Dis(AX) + Dis(XB)，这样一来，当我们遍历完所有节点X，Dis(AB)中记录的便是A到B的最短路径的距离。

很简单吧，代码看起来可能像下面这样：

代码如下:

for ( int i = 0; i < 节点个数; ++i )
{
    for ( int j = 0; j < 节点个数; ++j )
    {
        for ( int k = 0; k < 节点个数; ++k )
        {
            if ( Dis[i][k] + Dis[k][j] < Dis[i][j] )
            {
                // 找到更短路径
                Dis[i][j] = Dis[i][k] + Dis[k][j];
            }
        }
    }
}

但是这里我们要注意循环的嵌套顺序，如果把检查所有节点X放在最内层，那么结果将是不正确的，为什么呢？因为这样便过早的把i到j的最短路径确定下来了，而当后面存在更短的路径时，已经不再会更新了。

让我们来看一个例子，看下图：

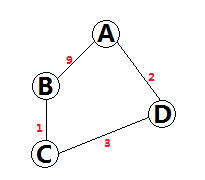
图中红色的数字代表边的权重。如果我们在最内层检查所有节点X，那么对于A->B，我们只能发现一条路径，就是A->B，路径距离为9。而这显然是不正确的，真实的最短路径是A->D->C->B，路径距离为6。造成错误的原因就是我们把检查所有节点X放在最内层，造成过早的把A到B的最短路径确定下来了，当确定A->B的最短路径时Dis(AC)尚未被计算。所以，我们需要改写循环顺序，如下：


代码如下:

for ( int k = 0; k < 节点个数; ++k )
{
    for ( int i = 0; i < 节点个数; ++i )
    {
        for ( int j = 0; j < 节点个数; ++j )
        {
            if ( Dis[i][k] + Dis[k][j] < Dis[i][j] )
            {
                // 找到更短路径
                Dis[i][j] = Dis[i][k] + Dis[k][j];
            }
        }
    }
}

这样一来，对于每一个节点X，我们都会把所有的i到j处理完毕后才继续检查下一个节点。

那么接下来的问题就是，我们如何找出最短路径呢？这里需要借助一个辅助数组Path，它是这样使用的：Path(AB)的值如果为P，则表示A节点到B节点的最短路径是A->...->P->B。这样一来，假设我们要找A->B的最短路径，那么就依次查找，假设Path(AB)的值为P，那么接着查找Path(AP)，假设Path(AP)的值为L，那么接着查找Path(AL)，假设Path(AL)的值为A，则查找结束，最短路径为A->L->P->B。

那么，如何填充Path的值呢？很简单，当我们发现Dis(AX) + Dis(XB) < Dis(AB)成立时，就要把最短路径改为A->...->X->...->B，而此时，Path(XB)的值是已知的，所以，Path(AB) = Path(XB)。

好了，基本的介绍完成了，接下来就是实现的时候了，这里我们使用图以及邻接矩阵：


代码如下:

#define INFINITE 1000           // 最大值
#define MAX_VERTEX_COUNT 20 　　// 最大顶点个数
//////////////////////////////////////////////////////////////////////////

struct Graph
{
    int     arrArcs[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];    // 邻接矩阵
    int     nVertexCount;                               　　// 顶点数量
    int     nArcCount;                                  　　// 边的数量
};
//////////////////////////////////////////////////////////////////////////
首先，我们写一个方法，用于读入图的数据：

void readGraphData( Graph *_pGraph )
{
    std::cout << "请输入顶点数量和边的数量: ";
    std::cin >> _pGraph->nVertexCount;
    std::cin >> _pGraph->nArcCount;

std::cout << "请输入邻接矩阵数据:" << std::endl;
    for ( int row = 0; row < _pGraph->nVertexCount; ++row )
    {
        for ( int col = 0; col < _pGraph->nVertexCount; ++col )
        {
            std::cin >> _pGraph->arrArcs[row][col];
        }
    }
}

接着，就是核心的Floyd算法：


代码如下:

void floyd( int _arrDis[][MAX_VERTEX_COUNT], int _arrPath[][MAX_VERTEX_COUNT], int _nVertexCount )
{
    // 先初始化_arrPath
    for ( int i = 0; i < _nVertexCount; ++i )
    {
        for ( int j = 0; j < _nVertexCount; ++j )
        {
            _arrPath[i][j] = i;
        }
    }
    //////////////////////////////////////////////////////////////////////////

for ( int k = 0; k < _nVertexCount; ++k )
    {
        for ( int i = 0; i < _nVertexCount; ++i )
        {
            for ( int j = 0; j < _nVertexCount; ++j )
            {
                if ( _arrDis[i][k] + _arrDis[k][j] < _arrDis[i][j] )
                {
                    // 找到更短路径
                    _arrDis[i][j] = _arrDis[i][k] + _arrDis[k][j];

_arrPath[i][j] = _arrPath[k][j];
                }
            }
        }
    }
}

OK，最后是输出结果数据代码：


代码如下:

void printResult( int _arrDis[][MAX_VERTEX_COUNT], int _arrPath[][MAX_VERTEX_COUNT], int _nVertexCount )
{
    std::cout << "Origin -> Dest   Distance    Path" << std::endl;

for ( int i = 0; i < _nVertexCount; ++i )
    {
        for ( int j = 0; j < _nVertexCount; ++j )
        {
            if ( i != j )   // 节点不是自身
            {
                std::cout << i+1 << " -> " << j+1 << "\t\t";
                if ( INFINITE == _arrDis[i][j] )    // i -> j 不存在路径
                {
                    std::cout << "INFINITE" << "\t\t";
                }
                else
                {
                    std::cout << _arrDis[i][j] << "\t\t";

// 由于我们查询最短路径是从后往前插，因此我们把查询得到的节点
                    // 压入栈中，最后弹出以顺序输出结果。
                    std::stack<int> stackVertices;
                    int k = j;

do
                    {
                        k = _arrPath[i][k];
                        stackVertices.push( k );
                    } while ( k != i );
                    //////////////////////////////////////////////////////////////////////////

std::cout << stackVertices.top()+1;
                    stackVertices.pop();

unsigned int nLength = stackVertices.size();
                    for ( unsigned int nIndex = 0; nIndex < nLength; ++nIndex )
                    {
                        std::cout << " -> " << stackVertices.top()+1;
                        stackVertices.pop();
                    }

std::cout << " -> " << j+1 << std::endl;
                }
            }
        }
    }
}

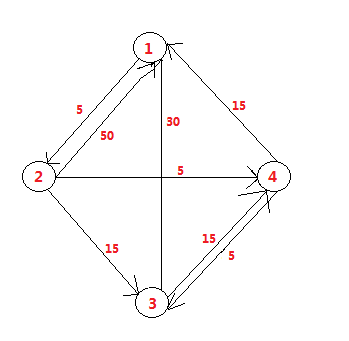
好了，是时候测试了，我们用的图如下：

测试代码如下：


代码如下:

int main( void )
{
    Graph myGraph;
    readGraphData( &myGraph );
    //////////////////////////////////////////////////////////////////////////

int arrDis[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];
    int arrPath[MAX_VERTEX_COUNT][MAX_VERTEX_COUNT];

// 先初始化arrDis
    for ( int i = 0; i < myGraph.nVertexCount; ++i )
    {
        for ( int j = 0; j < myGraph.nVertexCount; ++j )
        {
            arrDis[i][j] = myGraph.arrArcs[i][j];
        }
    }

floyd( arrDis, arrPath, myGraph.nVertexCount );
    //////////////////////////////////////////////////////////////////////////

printResult( arrDis, arrPath, myGraph.nVertexCount );
    //////////////////////////////////////////////////////////////////////////

system( "pause" );
    return 0;
}

如图：