在python Numpy中求向量和矩阵的范数实例

np.linalg.norm(求范数):linalg=linear（线性）+algebra（代数），norm则表示范数。

函数参数

x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)

①x: 表示矩阵（也可以是一维）

②ord：范数类型

向量的范数：

矩阵的范数：

ord=1：列和的最大值

ord=2：|λE-ATA|=0，求特征值，然后求最大特征值得算术平方根

ord=∞：行和的最大值

③axis：处理类型

axis=1表示按行向量处理，求多个行向量的范数

axis=0表示按列向量处理，求多个列向量的范数

axis=None表示矩阵范数。

④keepding：是否保持矩阵的二维特性

True表示保持矩阵的二维特性，False相反

向量范数:

1-范数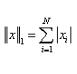： ，即向量元素绝对值之和，matlab调用函数norm(x, 1) 。

2-范数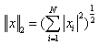： ，Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。

∞-范数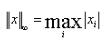： ，即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。

-∞-范数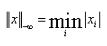： ，即所有向量元素绝对值中的最小值，matlab调用函数norm(x, -inf)。

p-范数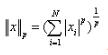： ，即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

矩阵范数:

1-范数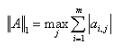： ， 列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数norm(A, 1)。

2-范数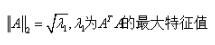： ，谱范数，即A'A矩阵的最大特征值的开平方。matlab调用函数norm(x, 2)。

∞-范数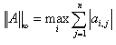： ，行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数norm(A, inf)。

F-范数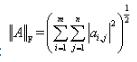： ，Frobenius范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数norm(A, 'fro‘)。

import numpy as np

x1=np.array([1,5,6,3,-1])
x2=np.arange(12).reshape(3,4)
print x1,'\n',x2
print '向量2范数:'
print np.linalg.norm(x1)
print np.linalg.norm(x1,ord=2)
print '默认的矩阵范数:'
print np.linalg.norm(x2)
print '矩阵2范数:'
print np.linalg.norm(x2,ord=2)

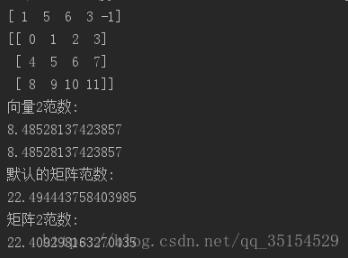
经测试知：

np.linalg.norm(X),X为向量时，默认求向量2范数，即求向量元素绝对值的平方和再开方；

X为矩阵是，默认求的是F范数。矩阵的F范数即：矩阵的各个元素平方之和再开平方根，它通常也叫做矩阵的L2范数，它的有点在它是一个凸函数，可以求导求解，易于计算。

以上这篇在python Numpy中求向量和矩阵的范数实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python numpy中矩阵的基本用法汇总

    Python numpy中矩阵的基本用法汇总

    Python矩阵的基本用法 mat()函数将目标数据的类型转化成矩阵(matrix) 1,mat()函数和array()函数的区别 Numpy函数库中存在两种不同的数据类型(矩阵matrix和数组array),都可以用于处理行列表示的数字元素,虽然他们看起来很相似,但是在这两个数据类型上执行相同的数学运算可能得到不同的结果,其中Numpy函数库中的matrix与MATLAB中matrices等价. 直接看一个例子: import numpy as np a = np.mat('1 3;5 7')

  • Python科学计算包numpy用法实例详解

    本文实例讲述了Python科学计算包numpy用法.分享给大家供大家参考,具体如下: 1 数据结构 numpy使用一种称为ndarray的类似Matlab的矩阵式数据结构管理数据,比python的列表和标准库的array类更为强大,处理数据更为方便. 1.1 数组的生成 在numpy中,生成数组需要指定数据类型,默认是int32,即整数,可以通过dtype参数来指定,一般用到的有int32.bool.float32.uint32.complex,分别代表整数.布尔值.浮点型.无符号整数和复数 一

  • Python numpy 提取矩阵的某一行或某一列的实例

    如下所示: import numpy as np a=np.arange(9).reshape(3,3) a Out[31]: array([[0, 1, 2], [3, 4, 5], [6, 7, 8]]) 矩阵的某一行 a[1] Out[32]: array([3, 4, 5]) 矩阵的某一列 a[:,1] Out[33]: array([1, 4, 7]) b=np.eye(3,3) b Out[36]: array([[ 1., 0., 0.], [ 0., 1., 0.], [ 0.,

  • numpy中矩阵合并的实例

    python中科学计算包numpy中矩阵的合并,需要用到如下两个函数: 列合并:np.column_stack() ,其中函数参数为一个tuple 行合并:np.row_stack(),其中函数参数为一个tuple >>> import numpy as np >>> a = np.arange(8).reshape(4, -1) >>> print(a) [[0 1] [2 3] [4 5] [6 7]] >>> b = np.ar

  • python中numpy的矩阵、多维数组的用法

    1. 引言 最近在将一个算法由matlab转成python,初学python,很多地方还不熟悉,总体感觉就是上手容易,实际上很优雅地用python还是蛮难的.目前为止,觉得就算法仿真研究而言,还是matlab用得特别舒服,可能是比较熟悉的缘故吧.matlab直接集成了很多算法工具箱,函数查询.调用.变量查询等非常方便,或许以后用久了python也会感觉很好用.与python相比,最喜欢的莫过于可以直接选中某段代码执行了,操作方便,python也可以实现,就是感觉不是很方便. 言归正传,做算法要用

  • Python:Numpy 求平均向量的实例

    如下所示: >>> import numpy as np >>> a = np.array([[1, 2, 3], [3, 1, 2]]) >>> b = np.array([[5, 2, 6], [5, 1, 2]]) >>> a array([[1, 2, 3], [3, 1, 2]]) >>> b array([[5, 2, 6], [5, 1, 2]]) >>> c = a + b >

  • 在python Numpy中求向量和矩阵的范数实例

    np.linalg.norm(求范数):linalg=linear(线性)+algebra(代数),norm则表示范数. 函数参数 x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False) ①x: 表示矩阵(也可以是一维) ②ord:范数类型 向量的范数: 矩阵的范数: ord=1:列和的最大值 ord=2:|λE-ATA|=0,求特征值,然后求最大特征值得算术平方根 ord=∞:行和的最大值 ③axis:处理类型 axis=1表

  • 详解Python NumPy中矩阵和通用函数的使用

    详解Python NumPy中矩阵和通用函数的使用

    目录 一.创建矩阵 二.从已有矩阵创建新矩阵 三.通用函数 四.算术运算 在NumPy中,矩阵是 ndarray 的子类,与数学概念中的矩阵一样,NumPy中的矩阵也是二维的,可以使用 mat . matrix 以及 bmat 函数来创建矩阵. 一.创建矩阵 mat 函数创建矩阵时,若输入已为 matrix 或 ndarray 对象,则不会为它们创建副本. 因此,调用 mat() 函数和调用 matrix(data, copy=False) 等价. 1) 在创建矩阵的专用字符串中,矩阵的行与行之

  • 浅谈python numpy中nonzero()的用法

    nonzero函数返回非零元素的目录. 返回值为元组, 两个值分别为两个维度, 包含了相应维度上非零元素的目录值. import numpy as np A = np.mat([[0,1,2,3,4,3,2,1,0],[0,1,2,3,4,5,6,7,0]]) x = A.nonzero() #取出矩阵中的非零元素的坐标 print x #输出是一个元组,两个维度.一一对应, #返回非零元素在矩阵中的位置,前一个列表存放非零行坐标,后一个列表存放非零元素列坐标 #(array([0, 0, 0,

  • Python numpy中的ndarray介绍

    Python numpy中的ndarray介绍

    目录 1. 什么是 ndarray? ndarray 概念 ndarray 内部关系 2. ndarray 内存结构 ndarray 内存结构 3. ndarray vs list ndarray 特点 list 特点 在上一期python numpy 模块中对概述介绍了numpy 模块安装.使用方法.特点等入门知识. numpy 模块是一个开源的第三方Python库,常用于科学和工程领域,是科学Python和PyData 生态系统的核心. numpy 模块易学易用的特点,基本上覆盖了初学者到先

  • Python Numpy中ndarray的常见操作

    Python Numpy中ndarray的常见操作

    目录 前言 0 Numpy基础知识 1 ndarray的属性 1.1 输出ndarray的常见属性 2 ndarray的数据类型 3 修改ndarray的形状和数据类型 3.1 查看和修改ndarray的形状 3.2 查看和修改ndarray的数据类型 4 ndarray数组创建 5 ndarray数组的常见运算 6 ndarray数组的索引.切片和迭代 7 ndarray数组的堆叠.拆分 前言 NumPy(Numerical Python)是Python的一种开源的数值计算扩展.这种工具可用来

  • Python numpy中np.random.seed()的详细用法实例

    Python numpy中np.random.seed()的详细用法实例

    目录 引言 E.G.实验 E.G.随机数种子参数的作用 补充:一个随机种子在代码中只作用一次,只作用于其定义位置的下一次随机数生成 总结 引言 在进行机器学习和深度学习中,我们会经常用到np.random.seed(),利用随机数种子,使得每次生成的随机数相同. numpy.randn.randn(d0,d1,...,dn) randn函数根据给定维度生成大概率在(-2.58~+2.58)之间的数据 randn函数返回一个或者一组样本,具有标准正态分布 dn表示每个维度 返回值为指定维度的arr

  • Python numpy生成矩阵、串联矩阵代码分享

    import numpy 生成numpy矩阵的几个相关函数: numpy.array() numpy.zeros() numpy.ones() numpy.eye() 串联生成numpy矩阵的几个相关函数: numpy.array() numpy.row_stack() numpy.column_stack() numpy.reshape() >>> import numpy >>> numpy.eye(3) array([[ 1., 0., 0.], [ 0., 1.

  • Python Numpy中数据的常用保存与读取方法

    在经常性读取大量的数值文件时(比如深度学习训练数据),可以考虑现将数据存储为Numpy格式,然后直接使用Numpy去读取,速度相比为转化前快很多. 下面就常用的保存数据到二进制文件和保存数据到文本文件进行介绍: 1.保存为二进制文件(.npy/.npz) numpy.save 保存一个数组到一个二进制的文件中,保存格式是.npy 参数介绍 numpy.save(file, arr, allow_pickle=True, fix_imports=True) file:文件名/文件路径 arr:要存

  • 在python中求分布函数相关的包实例

    为了了解(正态)分布的方法和属性,我们首先引入norm >>>from scipy.stats import norm >>>rv = norm() >>>dir(rv) # reformatted ['__class__', '__delattr__', '__dict__', '__doc__', '__getattribute__', '__hash__', '__init__', '__module__', '__new__', '__redu

  • python numpy中对ndarry按照index增删改查

    在numpy中的ndarry是一个数组,因此index就是位置下标,注意下标是从0开始 增加:在插入时使用np.insert(),在末尾添加时使用np.append() 删除:需要使用np.delete() 修改:直接指定下标 查找:直接指定下标 示例代码: import numpy as np if __name__ == '__main__':     array = np.array(["a", "b", "c", "d"

随机推荐