python机器学习GCN图卷积神经网络原理解析

目录

• 1. 图信号处理知识
• 1.1 图的拉普拉斯矩阵
• 1.1.1 拉普拉斯矩阵的定义及示例
• 1.1.2 正则化拉普拉斯矩阵
• 1.2 图上的傅里叶变换
• 1.3 图信号滤波器
• 2. 图卷积神经网络
• 2.1 数学定义
• 2.2 GCN的理解及时间复杂度
• 2.3 GCN的优缺点
• 3. Pytorch代码解析

1. 图信号处理知识

图卷积神经网络涉及到图信号处理的相关知识，也是由图信号处理领域的知识推导发展而来，了解图信号处理的知识是理解图卷积神经网络的基础。

1.1 图的拉普拉斯矩阵

拉普拉斯矩阵是体现图结构关联的一种重要矩阵，是图卷积神经网络的一个重要部分。

1.1.1 拉普拉斯矩阵的定义及示例

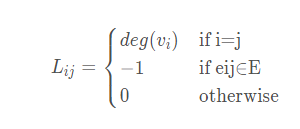
实例：

按照上述计算式子，可以得到拉普拉斯矩阵为：

1.1.2 正则化拉普拉斯矩阵

1.1.3 拉普拉斯矩阵的性质

1.2 图上的傅里叶变换

傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号。它将信号从时域转换到频域，从频域视角给出了信号处理的另一种解法。（1）对于图结构，可以定义图上的傅里叶变换(GFT)，对于任意一个在图G上的信号x，其傅里叶变换表示为：

从线代角度，可以清晰的看出：v1,…, vn构成了N维特征空间中的一组完备基向量，G中任意一个图信号都可表示为这些基向量的线性加权求和，系数为图信号对应傅里叶基上的傅里叶系数。

回到之前提到的拉普拉斯矩阵刻画平滑度的总变差：

可以看成：刻画图平滑度的总变差是图中所有节点特征值的线性组合，权值为傅里叶系数的平方。总变差取最小值的条件是图信号与最小的特征值所对应的特征向量完全重合，结合其描述图信号整体平滑度的意义，可将特征值等价成频率：特征值越低，频率越低，对应的傅里叶基变化缓慢，即相近节点的信号值趋于一致。

把图信号所有的傅里叶系数结合称为频谱(spectrum)，频域的视角从全局视角既考虑信号本身，也考虑到图的结构性质。

1.3 图信号滤波器

图滤波器(Graph Filter)为对图中的频率分量进行增强或衰减，图滤波算子核心为其频率响应矩阵，为滤波器带来不同的滤波效果。

故图滤波器根据滤波效果可分为低通，高通和带通。

低通滤波器：保留低频部分，关注信号的平滑部分；

高通滤波器：保留高频部分，关注信号的剧烈变化部分；

带通滤波器：保留特定频段部分；

而拉普拉斯矩阵多项式扩展可形成图滤波器H：

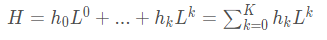
2. 图卷积神经网络

2.1 数学定义

图卷积运算的数学定义为：

上述公式存在一个较大问题：学习参数为N，这涉及到整个图的所有节点，对于大规模数据极易发生过拟合。

进一步的化简推导：将之前说到的拉普拉斯矩阵的多项式展开代替上述可训练参数矩阵。

此结构内容即定义为图卷积层(GCN layer)，有图卷积层堆叠得到的网络模型即为图卷积网络GCN。

2.2 GCN的理解及时间复杂度

图卷积层是对频率响应矩阵的极大化简，将本要训练的图滤波器直接退化为重归一化拉普拉斯矩阵

2.3 GCN的优缺点

优点：GCN作为近年图神经网络的基础之作，对处理图数据非常有效，其对图结构的结构信息和节点的属性信息同时学习，共同得到最终的节点特征表示，考虑到了节点之间的结构关联性，这在图操作中是非常重要的。

缺点：过平滑问题(多层叠加之后，节点的表示向量趋向一致，节点难以区分)，由于GCN具有一个低通滤波器的作用(j聚合特征时使得节点特征不断融合)，多次迭代后特征会趋于相同。

3. Pytorch代码解析

GCN层的pytorch实现：

class GraphConvolutionLayer(nn.Module):
    '''
        图卷积层:Lsym*X*W
            其中 Lsym表示正则化图拉普拉斯矩阵, X为输入特征, W为权重矩阵, X'表示输出特征;
            *表示矩阵乘法
    '''
    def __init__(self, input_dim, output_dim, use_bias=True):
        #初始化, parameters: input_dim-->输入维度, output_dim-->输出维度, use_bias-->是否使用偏置项, boolean
        super(GraphConvolutionLayer,self).__init__()
        self.input_dim=input_dim
        self.output_dim=output_dim
        self.use_bias=use_bias #是否加入偏置, 默认为True
        self.weight=nn.Parameter(torch.Tensor(input_dim, output_dim))#权重矩阵为可训练参数
        if self.use_bias==True: #加入偏置
            self.bias=nn.Parameter(torch.Tensor(output_dim))
        else: #设置偏置为空
            self.register_parameter('bias', None)
        self.reset_parameters()
    def reset_parameters(self):
        #初始化参数
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv, stdv)#使用均匀分布U(-stdv,stdv)初始化权重Tensor
        if self.bias is not None:
            self.bias.data.uniform_(-stdv, stdv)
    def forward(self, adj, input_feature):
        #前向传播, parameters: adj-->邻接矩阵(输入为正则化拉普拉斯矩阵), input_future-->输入特征矩阵
        temp=torch.mm(input_feature, self.weight)#矩阵乘法, 得到X*W
        output_feature=torch.sparse.mm(adj, temp)#由于邻接矩阵adj为稀疏矩阵, 采用稀疏矩阵乘法提高计算效率, 得到Lsym*temp=Lsym*X*W
        if self.use_bias==True: #若设置了偏置, 加入偏置项
            output_feature+=self.bias
        return output_feature

定义两层的GCN网络模型：

class GCN(nn.Module):
    '''
        定义两层GCN网络模型
    '''
    def __init__(self, input_dim, hidden_dim, output_dim):
        #初始化, parameters: input_dim-->输入维度, hidden_dim-->隐藏层维度, output_dim-->输出维度
        super.__init__(GCN, self).__init__()
        #定义两层图卷积层
        self.gcn1=GraphConvolutionLayer(input_dim, hidden_dim)
        self.gcn2=GraphConvolutionLayer(hidden_dim, output_dim)
    def forward(self, adj, feature):
        #前向传播, parameters: adj-->邻接矩阵, feature-->输入特征
        x=F.relu(self.gcn1(adj, feature))
        x=self.gcn2(adj, x)
        return F.log_softmax(x, dim=1)

以上就是GCN图卷积神经网络原理及代码解析的详细内容，更多关于GCN图卷积神经网络的资料请关注我们其它相关文章！