C语言三种方法解决轮转数组问题

目录

• 题目
• 1.题目描述
• 2.要求
• 3.原题链接
• 二、相关知识点
• 三、解决思路
• 旋转法
• 直接法
• 空间换取时间

题目

1.题目描述

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入:

nums = [1,2,3,4,5,6,7], k = 3

输出:

[5,6,7,1,2,3,4]

解释:

向右轮转 1 步: [7,1,2,3,4,5,6]

向右轮转 2 步: [6,7,1,2,3,4,5]

向右轮转 3 步: [5,6,7,1,2,3,4]

2.要求

进阶：

• 尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。
• 你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

3.原题链接

189. 轮转数组 - 力扣（LeetCode） (leetcode-cn.com)

二、相关知识点

本题实际上涉及到了复杂度的问题，包括时间复杂度和空间复杂度。

三、解决思路

旋转法

最优思路，这需要我们有较好的理解力了，可以把数组分为三个部分

假设我们需要选择k个数字：

1.后k个数字逆置

2.前n-k个数字逆置

3.整体逆置

此方法为最优法。符合题目要求

以示例 1为例子说明：

1 2 3 4 5 6 7//旋转3个数字
1 2 3 4 7 6 5//后k个数字逆置
4 3 2 1 7 6 5//前n-k个数字逆置
5 6 7 1 2 3 4//整体逆置

源代码如下：

void reverse(int*nums,int left,int right)
{
    while(left<right)
    {
        int tmp = nums[left];
        nums[left]=nums[right];
        nums[right] = tmp;
        ++left;
        --right;
    }
}
void rotate(int* nums, int numsSize, int k){
    k%=numsSize;
    reverse(nums,0,numsSize-k-1);
    reverse(nums,numsSize-k,numsSize-1);
    reverse(nums,0,numsSize-1);
}

注意点：k的大小可能大于数组的大小，所以我们要取模！

这个算法的时间复杂度为O（N），空间复杂度为O（1）

附上结果运行图：

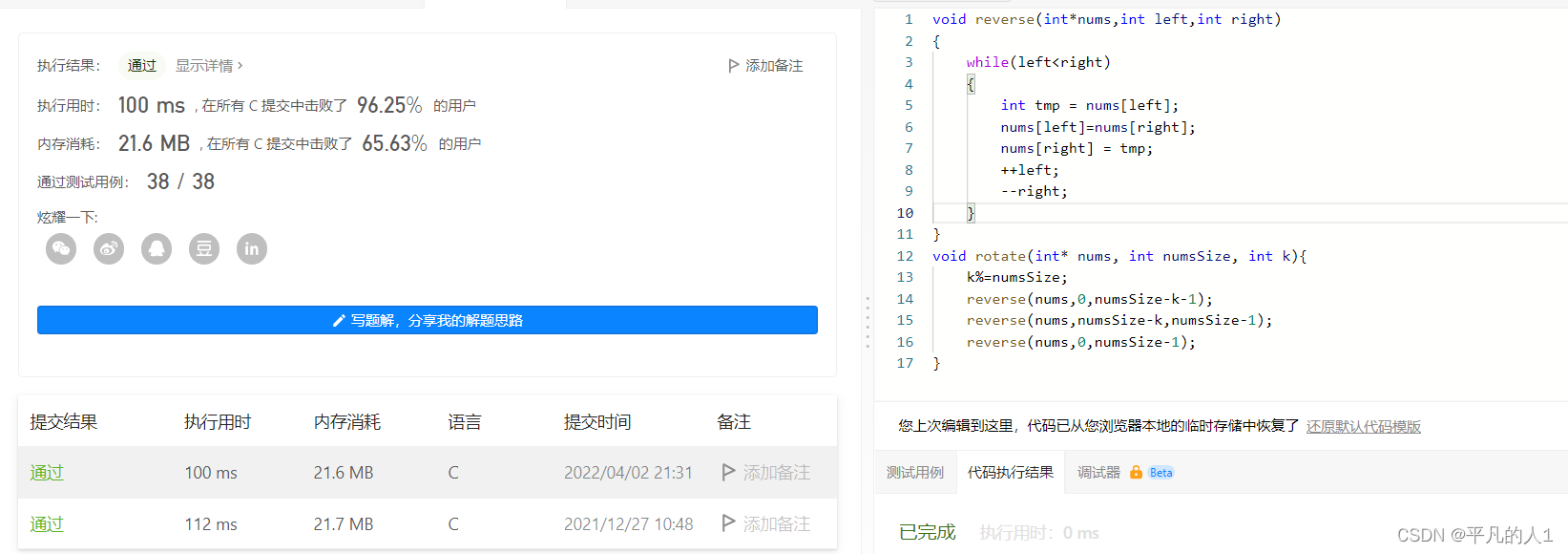
直接法

看到这道题，我们的第一种想法就是直接去旋转，当k=1是。我们就直接把最后一位的数字移动第一位，然后第二位开始往后移动，我们可以创建一个临时的变量来记录当前的最后一位，当k很大时，我们自然就是用循环去做，这是每个人都能想得到的一种方法

代码如下

void rotate(int* nums, int numsSize, int k){
    k %=numsSize;
  while(k--){
      int tmp = nums[numsSize-1];
      for(int end = numsSize-2;end>=0;--end){
          nums[end+1] = nums[end];
      }
      nums[0] = tmp;
  }
}

遗憾的是，这种算法的空间复杂（k*N），没能跑得过去，超时了，给出运行结果图

空间换取时间

以空间换取时间，这是比较常见的，就是额外开辟一个数组，存放选择的几个数字，然后将之前的数据存储到该数组的后半部分。最后将新数组拷贝到原来的数组中

代码如下

void rotate(int* nums, int numsSize, int k){
   k %= numsSize;
   int *newnum = (int*)malloc(sizeof(int)*numsSize);
   int j = 0;
   for(int i =numsSize-k;i<numsSize;i++){
       newnum[j++] =nums[i];
   }
   for(int i = 0;i<numsSize-k;i++){
       newnum[i+k] = nums[i];
   }
   memcpy(nums,newnum,sizeof(int)*numsSize);
}

运行结果如图

虽然也是通过了，但是效率不如思路一。

到此这篇关于C语言三种方法解决轮转数组问题 的文章就介绍到这了,更多相关C语言轮转数组内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！