OpenGL实现贝塞尔曲线或曲面

本文实例为大家分享了OpenGL实现贝塞尔曲线或曲面的具体代码，供大家参考，具体内容如下

理论基础

贝塞尔曲线和曲面：OpenGL只能直接绘制基本图元，对于曲线和曲面我们一般采用一系列线段或多边形来模拟的，这样当线段或多边形增多时必定很耗性能。其实对于这种曲线和曲面，我们可以使用一些控制点，通过求值器程序先计算出坐标等信息，然后直接用这些数据绘制，这样不仅节省内存，还提高了模拟曲线或曲面的精度(本质还是通过线段或多边形绘制的，只是求值器提前算出了曲线或曲面的顶点信息)。

求值器使用一般步骤：1.启用求值器 2.定义求值器 3.执行求值器。

注释：OpenGl3.1后，本节内容都已经废弃了，这些顶点着色器都可以实现了。

代码示例

1、曲线

#include "GLTools.h"

#ifdef __APPLE__
#include <glut/glut.h>
#else
#define FREEGLUT_STATIC
#include <GL/glut.h>
#endif

//控制点
GLfloat ctrlpoints[4][3] = {
 { -4.0, -4.0, 0.0}, { -2.0, 4.0, 0.0},
 {2.0, -4.0, 0.0}, {4.0, 4.0, 0.0}};

void init(void)
{
 glClearColor(0.0, 0.0, 0.0, 0.0);
 glShadeModel(GL_FLAT);
 //定义一维求值器
 glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
 //启动求职器
 glEnable(GL_MAP1_VERTEX_3);
}

void display(void)
{
 int i;

 glClear(GL_COLOR_BUFFER_BIT);
 glColor3f(1.0, 1.0, 1.0);
 glBegin(GL_LINE_STRIP);
 for (i = 0; i <= 30; i++)
  glEvalCoord1f((GLfloat) i/30.0);//执行求值器，每执行一次产生一个坐标
 glEnd();

 //绘制4个控制点
 glPointSize(5.0);
 glColor3f(1.0, 1.0, 0.0);
 glBegin(GL_POINTS);
 for (i = 0; i < 4; i++)
  glVertex3fv(&ctrlpoints[i][0]);
 glEnd();
 glFlush();
}

void reshape(int w, int h)
{
 glViewport(0, 0, (GLsizei) w, (GLsizei) h);
 glMatrixMode(GL_PROJECTION);
 glLoadIdentity();
 if (w <= h)
  glOrtho(-5.0, 5.0, -5.0*(GLfloat)h/(GLfloat)w,
    5.0*(GLfloat)h/(GLfloat)w, -5.0, 5.0);
 else
  glOrtho(-5.0*(GLfloat)w/(GLfloat)h,
    5.0*(GLfloat)w/(GLfloat)h, -5.0, 5.0, -5.0, 5.0);
 glMatrixMode(GL_MODELVIEW);
 glLoadIdentity();
}

void keyboard(unsigned char key, int x, int y)
{
 switch (key) {
  case 27:
   exit(0);
   break;
 }
}

int main(int argc, char** argv)
{
 glutInit(&argc, argv);
 glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
 glutInitWindowSize (500, 500);
 glutInitWindowPosition (100, 100);
 glutCreateWindow (argv[0]);
 init ();
 glutDisplayFunc(display);
 glutReshapeFunc(reshape);
 glutKeyboardFunc (keyboard);
 glutMainLoop();
 return 0;
}

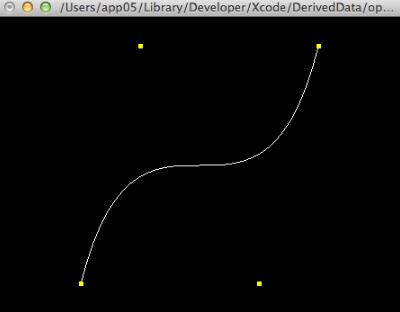
2、曲面

#include "GLTools.h"

#ifdef __APPLE__
#include <glut/glut.h>
#else
#define FREEGLUT_STATIC
#include <GL/glut.h>
#endif

GLfloat ctrlpoints[4][4][3] = {
 {{ -1.5, -1.5, 4.0}, { -0.5, -1.5, 2.0},
  {0.5, -1.5, -1.0}, {1.5, -1.5, 2.0}},
 {{ -1.5, -0.5, 1.0}, { -0.5, -0.5, 3.0},
  {0.5, -0.5, 0.0}, {1.5, -0.5, -1.0}},
 {{ -1.5, 0.5, 4.0}, { -0.5, 0.5, 0.0},
  {0.5, 0.5, 3.0}, {1.5, 0.5, 4.0}},
 {{ -1.5, 1.5, -2.0}, { -0.5, 1.5, -2.0},
  {0.5, 1.5, 0.0}, {1.5, 1.5, -1.0}}
};

GLfloat texpts[2][2][2] = {{{0.0, 0.0}, {0.0, 1.0}},
 {{1.0, 0.0}, {1.0, 1.0}}};

void display(void)
{
 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
 glColor3f(1.0, 1.0, 1.0);
 glEvalMesh2(GL_FILL, 0, 20, 0, 20);//glMapGrid2f()均匀产生坐标值，这里执行绘制
 glFlush();
}

#define imageWidth 64
#define imageHeight 64
GLubyte image[3*imageWidth*imageHeight];
//纹理数据
void makeImage(void)
{
 int i, j;
 float ti, tj;

 for (i = 0; i < imageWidth; i++) {
  ti = 2.0*3.14159265*i/imageWidth;
  for (j = 0; j < imageHeight; j++) {
   tj = 2.0*3.14159265*j/imageHeight;

   image[3*(imageHeight*i+j)] = (GLubyte) 127*(1.0+sin(ti));
   image[3*(imageHeight*i+j)+1] = (GLubyte) 127*(1.0+cos(2*tj));
   image[3*(imageHeight*i+j)+2] = (GLubyte) 127*(1.0+cos(ti+tj));
  }
 }
}

void init(void)
{
 //定义了两个求值器程序
 glMap2f(GL_MAP2_VERTEX_3, 0, 1, 3, 4,
   0, 1, 12, 4, &ctrlpoints[0][0][0]);
 glMap2f(GL_MAP2_TEXTURE_COORD_2, 0, 1, 2, 2,
   0, 1, 4, 2, &texpts[0][0][0]);
 glEnable(GL_MAP2_TEXTURE_COORD_2);
 glEnable(GL_MAP2_VERTEX_3);
 glMapGrid2f(20, 0.0, 1.0, 20, 0.0, 1.0);//均匀产生坐标

 //纹理属性设置
 makeImage();
 glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_DECAL);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
 glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
 glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, imageWidth, imageHeight, 0, GL_RGB, GL_UNSIGNED_BYTE, image);
 glEnable(GL_TEXTURE_2D);
 glEnable(GL_DEPTH_TEST);
 glShadeModel (GL_FLAT);
}

void reshape(int w, int h)
{
 glViewport(0, 0, (GLsizei) w, (GLsizei) h);
 glMatrixMode(GL_PROJECTION);
 glLoadIdentity();
 if (w <= h)
  glOrtho(-4.0, 4.0, -4.0*(GLfloat)h/(GLfloat)w,
    4.0*(GLfloat)h/(GLfloat)w, -4.0, 4.0);
 else
  glOrtho(-4.0*(GLfloat)w/(GLfloat)h,
    4.0*(GLfloat)w/(GLfloat)h, -4.0, 4.0, -4.0, 4.0);
 glMatrixMode(GL_MODELVIEW);
 glLoadIdentity();
 glRotatef(85.0, 1.0, 1.0, 1.0);
}

void keyboard(unsigned char key, int x, int y)
{
 switch (key) {
  case 27:
   exit(0);
   break;
 }
}

int main(int argc, char** argv)
{
 glutInit(&argc, argv);
 glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
 glutInitWindowSize (500, 500);
 glutInitWindowPosition (100, 100);
 glutCreateWindow (argv[0]);
 init ();
 glutDisplayFunc(display);
 glutReshapeFunc(reshape);
 glutKeyboardFunc(keyboard);
 glutMainLoop();
 return 0;

}

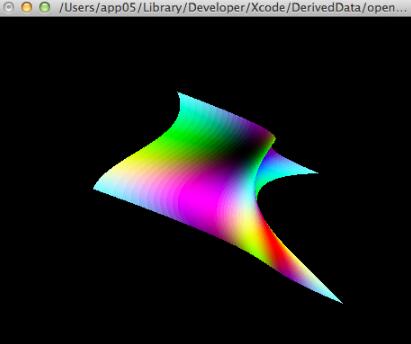
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。