C/C++后端学习与练习深入

目录

• 一、算法训练
• 1.拓扑顺序
• 2.功夫传人
• 3.二叉树中的最低公共祖先
• 二、工程项目训练
• day1.Qt(串口的使用)
• 三、总结

一、算法训练

首先给大家带来校招程序员考察的核心技能训练:算法,不管你用什么语言,

数据结构与算法一定是最核心的基本功。说得实际和功利一点， 算法是你进入大厂的敲门砖，还能帮你在工作中快速地弯道超车， 所以一定得搞懂哦~~~ 另外现在现在大厂的笔试很多采用ACM模式,面试手撕代码则多为力扣模式 (核心代码模式)今天给大家带来中大厂笔试训练

1.拓扑顺序

这是 2018 年研究生入学考试中给出的一个问题：

以下哪个选项不是从给定的有向图中获得的拓扑序列？

现在，请你编写一个程序来测试每个选项。
输入格式
第一行包含两个整数 N 和 M，分别表示有向图的点和边的数量。

接下来 M 行，每行给出一条边的起点和终点。

点的编号从 1 到 N。

再一行包含一个整数 K，表示询问次数。

接下来 K 行，每行包含一个所有点的排列。

一行中的数字用空格隔开。

输出格式
在一行中输出所有不是拓扑序列的询问序列的编号。

询问序列编号从 0 开始。

行首和行尾不得有多余空格，保证存在至少一个解。

数据范围
1≤N≤1000,
1≤M≤10000,
1≤K≤100
输入样例：
6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6
输出样例：
3 4

解析:首先了解一下拓扑排序的定义:在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

1.每个顶点出现且只出现一次。

2.若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

//这题根据条件性质解题即可
#include<bits/stdc++.h>
using namespace std;
const int N=10050;
int nodes[N],a[N],b[N],p[N];
int n,m;
int main()
{
	cin>>n>>m;
	int i,j;
    for(i=0;i<m;i++)
	{
		cin>>a[i]>>b[i];
	}
	int k;
	cin>>k;
	bool flag;
	vector<int> v;
	for(i=0;i<k;i++)
	{
		 flag=1;
		 for(j=1;j<=n;j++)
		 {
		 	cin>>nodes[j];
		 	p[nodes[j]]=j;
		 }
		 for(j=0;j<m;j++)
		{
			if(p[a[j]]>p[b[j]])
			flag=0;
		}
		if(!flag)
		v.push_back(i);
	}
	for(i=0;i<v.size();i++)
	{
		if(i==0) cout<<v[i];
		else cout<<" "<<v[i];
	}
    cout<<endl;
}

2.功夫传人

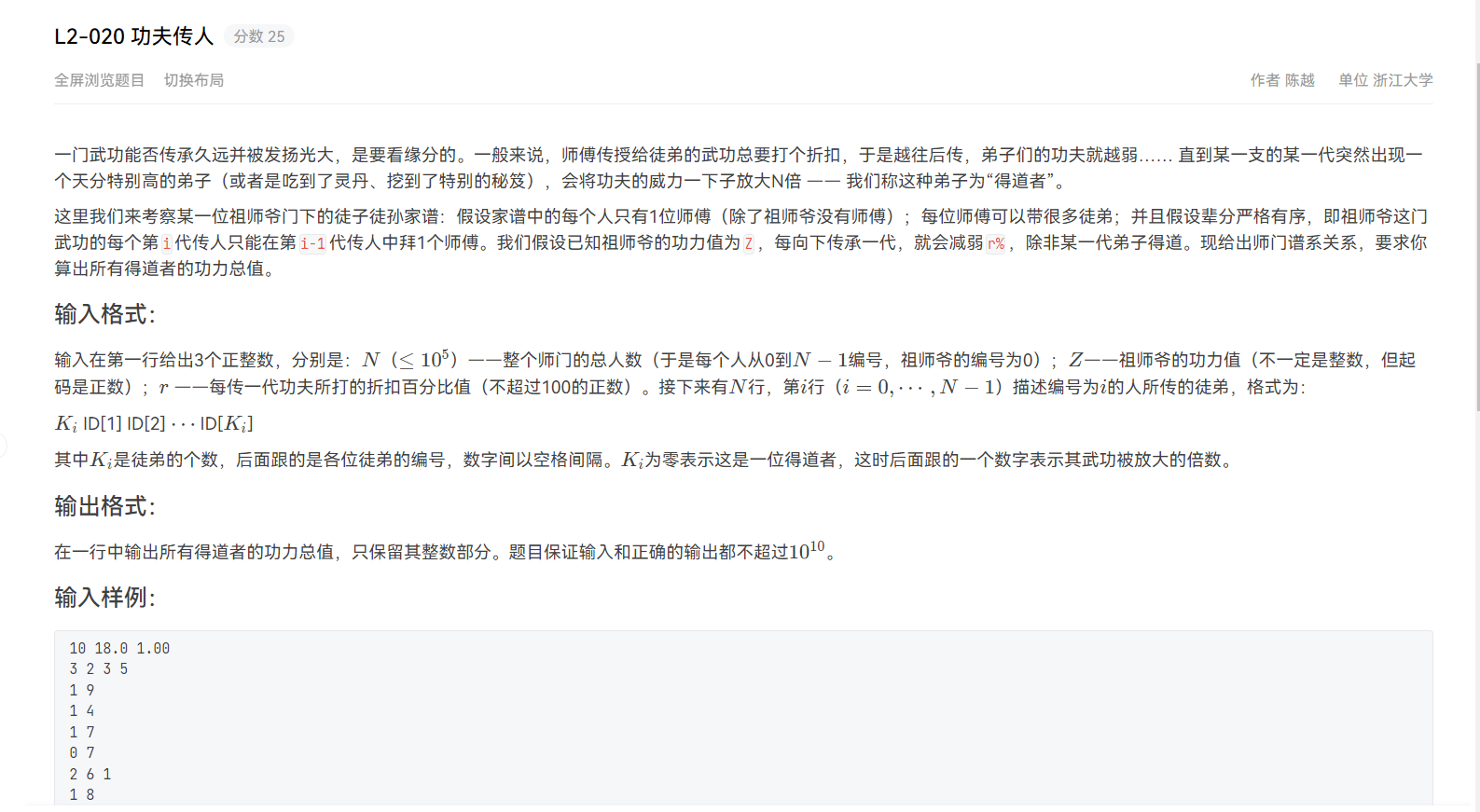
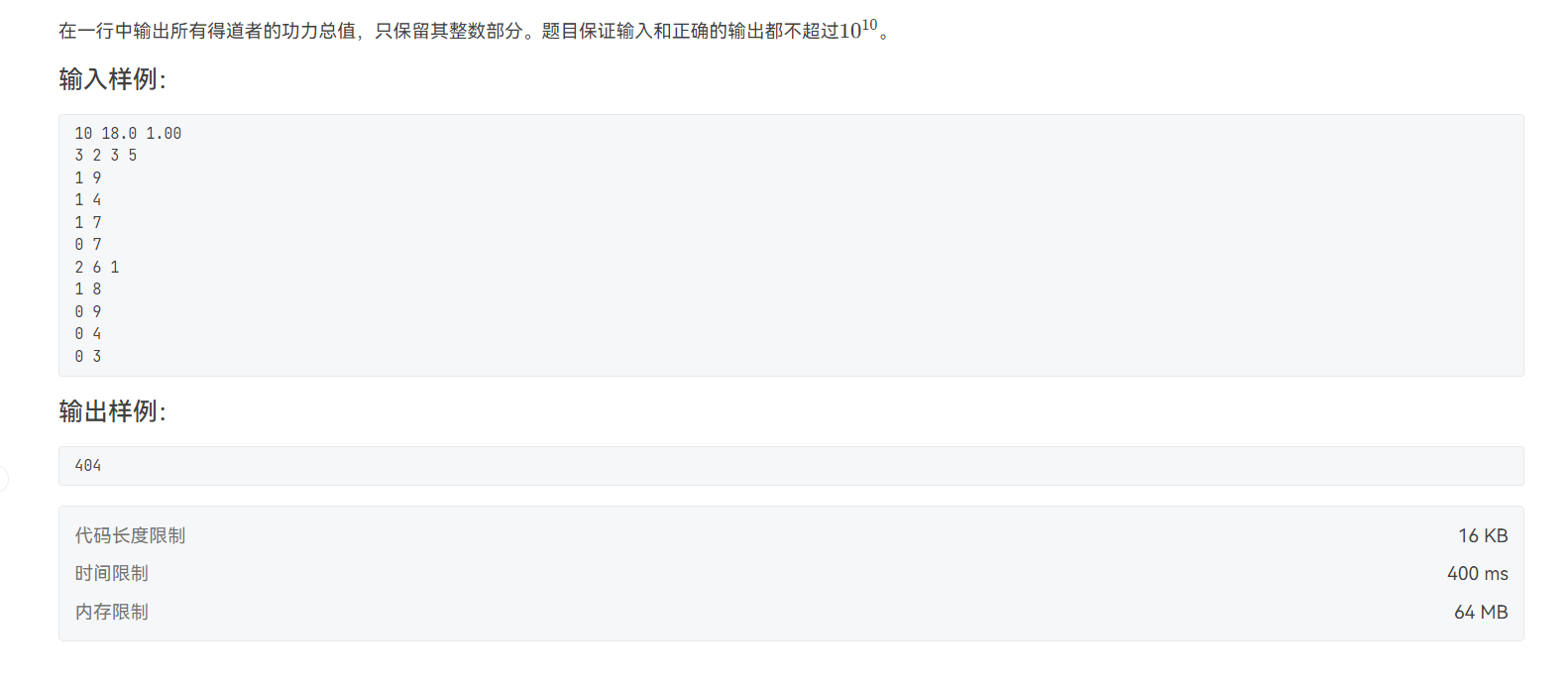
//这题用邻接表存储一下信息,然后再dfs配合回溯即可
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+50;
vector<int> v[N];
int n,st[N];
double z,r,sum;
void dfs(int u,double p)
{
	if(st[u])
	{
		sum+=p*v[u][0];
		return;
	}
	for(int i=0;i<v[u].size();i++)
	dfs(v[u][i],p*(1-r/100));
}
int main()
{
    cin>>n>>z>>r;
    int i,x;
    for(i=0;i<n;i++)
    {
      int k;
      cin>>k;
      if(k==0)
      {
      	 st[i]=1;
      	 cin>>x;
         v[i].push_back(x);
	  }
      else
     {
      while(k--)
      {
        cin>>x;
        v[i].push_back(x);
	  }
      }
    }
    dfs(0,z);
    cout<<(int)sum;
}

3.二叉树中的最低公共祖先

树中两个结点 U 和 V 的最低公共祖先（LCA）是指同时具有 U 和 V 作为后代的最深结点。

给定二叉树中的任何两个结点，请你找到它们的 LCA。

输入格式
第一行包含两个整数 M 和 N，分别表示询问结点对数以及二叉树中的结点数量。

接下来两行，每行包含 N 个不同的整数，分别表示二叉树的中序和前序遍历。

保证二叉树可由给定遍历序列唯一确定。

接下来 M 行，每行包含两个整数 U 和 V，表示一组询问。

所有结点权值均在 int 范围内。

输出格式
对于每对给定的 U 和 V，输出一行结果。

如果 U 和 V 的 LCA 是 A，且 A 不是 U 或 V，则输出 LCA of U and V is A.

如果 U 和 V 的 LCA 是 A，且 A 是 U 或 V 中的一个，则输出 X is an ancestor of Y.其中 X 表示 A，Y 表示另一个结点。

如果 U 或 V 没有在二叉树中找到，则输出 ERROR: U is not found. 或 ERROR: V is not found. 或 ERROR: U and V are not found.

数据范围
1≤M≤1000,
1≤N≤10000
输入样例：
6 8
7 2 3 4 6 5 1 8
5 3 7 2 6 4 8 1
2 6
8 1
7 9
12 -3
0 8
99 99
输出样例：
LCA of 2 and 6 is 3.
8 is an ancestor of 1.
ERROR: 9 is not found.
ERROR: 12 and -3 are not found.
ERROR: 0 is not found.
ERROR: 99 and 99 are not found.

//常规方法建树再按题目要求做即可
#include<bits/stdc++.h>
using  namespace std;
const int N=1e4+50;
int m,n;
int in[N],pre[N],depth[N],p[N];
int build(int il,int ir,int pl,int pr,int d)
{
	int root=pre[pl];
	int k=root;
	depth[root]=d;
	if(il<k) p[build(il,k-1,pl+1,pl+1+(k-1-il),d+1)]=root;
	if(k<ir) p[build(k+1,ir,pl+1+(k-1-il)+1,pr,d+1)]=root;
	return root;
}
unordered_map<int,int> pos;
int main()
{
	cin>>m>>n;
	int i;
	for(i=0;i<n;i++)
   {
   	  cin>>in[i];
   	  pos[in[i]]=i;
   }
   for(i=0;i<n;i++)
   {
   	  cin>>pre[i];
   	  pre[i]=pos[pre[i]];
   }
   int a,b,x,y;
   build(0,n-1,0,n-1,0);
   while(m--)
   {
     	cin>>a>>b;
	    x=a,y=b;
	    if(pos.count(a)&&pos.count(b))
	    {
	    	a=pos[a],b=pos[b];
	    	x=a,y=b;
	          while(a!=b)
	    	{
	    		if(depth[a]>depth[b])
	    		a=p[a];
	    		else
	    		b=p[b];
			}
			if(a!=x&&a!=y)
			printf("LCA of %d and %d is %d.\n",in[x],in[y],in[a]);
			else if(a==x)
			printf("%d is an ancestor of %d.\n",in[x],in[y]);
			else
			printf("%d is an ancestor of %d.\n",in[y],in[x]);
		}
		else if(pos.count(a)==0&&pos.count(b)==0)
		printf("ERROR: %d and %d are not found.\n",x,y);
		else if(pos.count(a)==0)
		printf("ERROR: %d is not found.\n",x);
		else
		printf("ERROR: %d is not found.\n",y);
   }
}

二、工程项目训练

项目&实习对于秋招来说意义重大,一份好的实习可以让招聘方看到你的工作能力：

Tips:工作能力:工作能力指的是你工作相关的能力，是在目标岗位上的专业能力，通过实习可以积累你的实战经验，也可以向公司表明你在实际工作中的实操能力。

但是没有实习也并不代表你秋招无法找到一份好的工作:

你可以将在校期间的社团、竞赛等相关在校经历补充在简历上；另外如果掌握某种和工作相关的知识或技能，也要尽可能写得详细一些，一定要表明你是如何把上述这些知识技能运用于工作中的。这样可以表现出你很善于学习新知识的特点，给自己加印象分。另外要勤做项目,使自己的项目经历与自己求职的目标岗位相契合,当我们能在简历中通过自己过往的经历证明自己的能力优势，并且这个能力优势又是企业需要的，那么我们拿到面试机会的可能性就会很大。

下面由小学徒给大家带来Qt的项目学习秘籍,希望大家喜欢。

day1.Qt(串口的使用)

这里必须夸下Qt Creator的帮助(不同于其他IDE帮助需要联网)

学习图形界面开发，肯定离不开帮助文档的使用，因为它不像 C 语言那样就那么几个函数接口(api)，图形接口的接口可以用海量来形容，但我们只需要记住常用的几个即可,君子性非异也，善假于物也。

大家要善于借助外物的力量，遇到不熟悉的直接去帮助文挡查看用法。

我们在日常使用中使用 Qt 帮助文档，有几个需要关注的点:

1)类使用的相关介绍

2)查看部件的信号

3)查看部件的事件(其所对应的虚函数如何编写)

4)查看所用部件(类)的相应成员函数(功能，参数，返回值)

1)类使用的相关介绍

Qt另一个方便之处在于光标移动到类名字的地方，接着按“F1”即可跳转到所对应的帮助文件：

可将光标移到类名字这里,然后按F1即可跳转到所对应的帮助文档。

2)查看部件的信号

以QplainTextEdit(纯文本输入框)为例我们来看到它的公有函数　

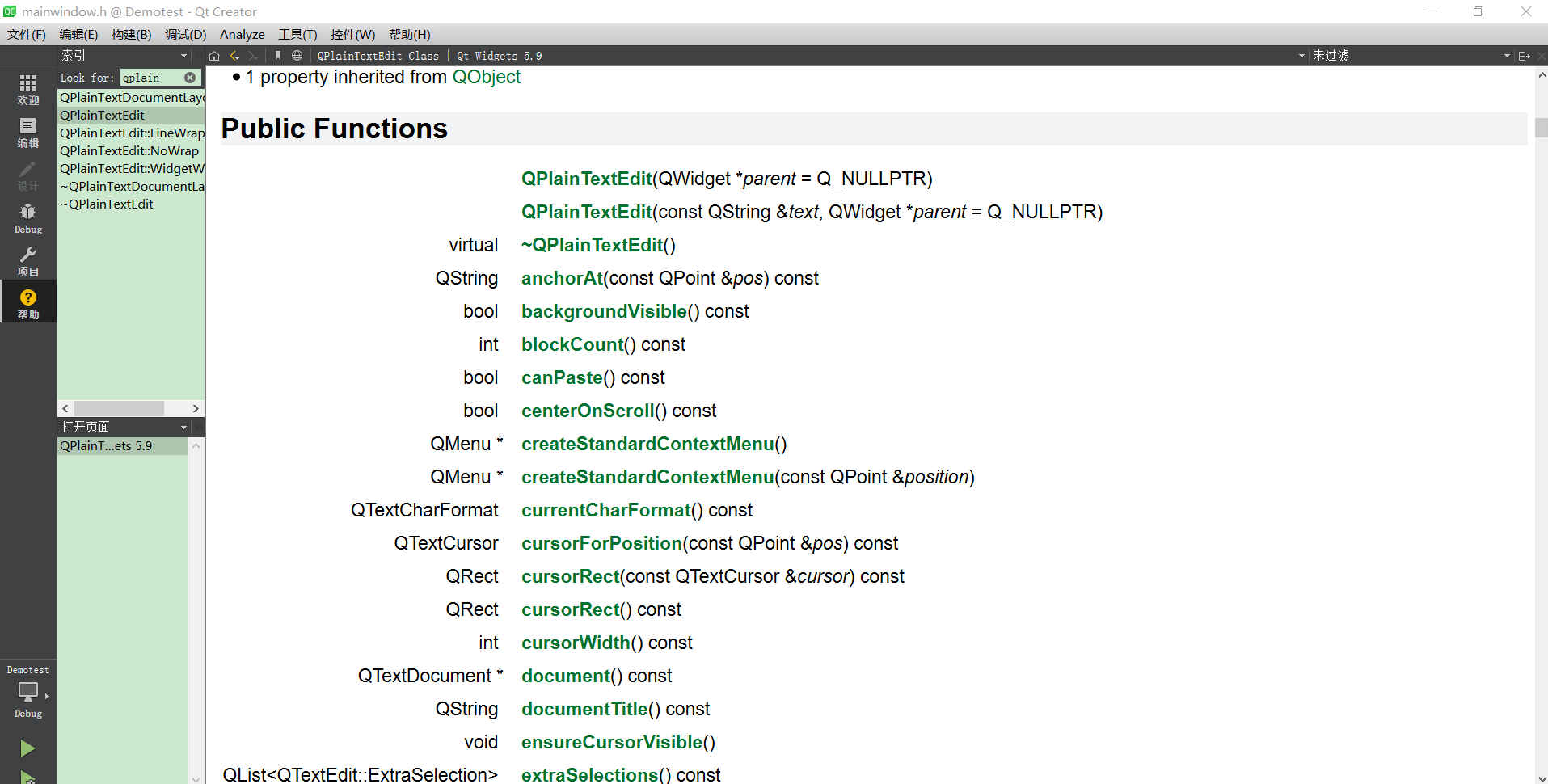
公有函数:共有成员可以被程序中的任何代码访问等等

Summary:Qt上手还是非常的容易，自带的帮助文档中的内容非常详细，还有示例代码，如果想着重学习UI的话:Qt Designer能让你通过以拖动控件放置的方式，可视化的设计UI界面，当你设计好界面编译完成后，在构建目录中会找到文件名形如“ui_XXXX.h”的头文件，这是Qt根据你的UI，自动帮你生成的C++代码，内容就是UI的C++实现方式，大家可以跟着它自动生成的这段代码学来学习UI是怎么实现的，这个比自己看文档要来的直观很多。而且对于初学者来说一个可拖拽位置可改变尺寸的有趣窗口要比一个黑框控制台程序要有意思的多。

三、总结

到此这篇关于C/C++后端学习与练习深入的文章就介绍到这了,更多相关C++后端内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！