详解Java中AC自动机的原理与实现

目录

• 简介
• 工作过程
• 数据结构
• 初始化
• 构建字典树
• 构建失败指针
• 匹配
• 执行结果

简介

AC自动机是一个多模式匹配算法，在模式匹配领域被广泛应用，举一个经典的例子，违禁词查找并替换为***。AC自动机其实是Trie树和KMP 算法的结合,首先将多模式串建立一个Tire树，然后结合KMP算法前缀与后缀匹配可以减少不必要比较的思想达到高效找到字符串中出现的匹配串。

如果不知道什么是Tire树，可以先查看：详解Java中字典树(Trie树)的图解与实现

如果不知道KMP算法，可以先查看：详解Java中KMP算法的图解与实现

工作过程

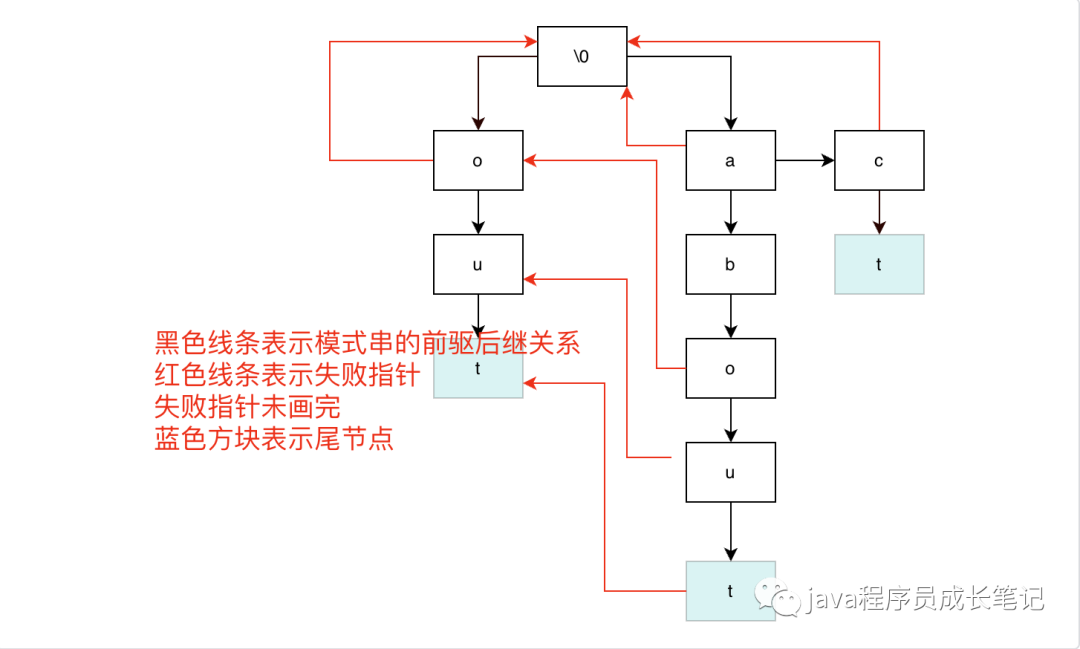
首先看一下AC自动机的结构，从造型上看，跟我们之前讲Tire树几乎一样，但是多了红色线条（这里因为画完太乱，没有画完），这个红色线条我们称为失败指针。其匹配规则与KMP一致，后缀和前缀的匹配，不一样的是，KMP是同一个模式串的前缀和后缀进行匹配，而这里是当前模式串的后缀，与另一个模式串的前缀进行匹配。如果能够匹配上，因为这两个模式串的前缀一定不同（相同的前缀已经聚合），将当前已匹配的后缀拿出来，比如abo，后缀为o，bo，abo，这时候我们再找另一个模式串的最长前缀与当前后缀匹配上（对应kmp中的最长前缀后缀子串），这时候我们可以找到out的o，则about中的o节点的失败指针指向out的o节点，这么做的意义就是主串可以一直往后比较，不用往前回溯（比如ab，之前匹配过能匹配上，但是到o是失败了，其他匹配串不可能出现ab前缀，所以不必再匹配，一定失败）。

构建过程：建立一棵Tire树，结尾节点需要标志当前模式串的长度，构建失败指针。

查找过程：从根节点出发，查找当前节点的孩子节点是否有与当前字符匹配的字符，匹配则判断是否为尾节点，是则匹配成功，记录。不是尾节点继续匹配。如果孩子节点没有与字符匹配的，则直接转到失败指针继续操作。

数据结构

一个value记录当前节点的值，childNode记录当前节点的子节点（假设仅出现26个小写字母，空间存在浪费，可使用hash表，有序二分，跳表进行优化），isTail标志当前节点是否为尾节点，failNode表示失败指针，即当前节点的孩子节点与当前字符均不匹配的时候，转到哪个节点接续进行匹配，tailLength，记录模式串的长度，方便快速拿出模式串的值（根据长度以及匹配的index，从主串中拿）。

public static class Node{
       //当前节点值
       private char value;
       //当前节点的孩子节点
       private Node[] childNode;
       //标志当前节点是否是某单词结尾
       private boolean isTail;
       //失败指针
       private Node failNode;
       //匹配串长度，当isTail==true时，表示从root当当前位置是一个完整的匹配串，记录这个匹配串的长度，便于之后快速找到匹配串
       private Integer tailLength;
       public Node(char value) {
           this.value = value;
      }
  }

初始化

初始化一棵仅存在root的根节点，root的失败指针以及长度均为null。

Node root;
   public void init() {
       root = new Node('\0');
       root.childNode = new Node[26];
  }

构建字典树

这个过程之前Tire树中已经讲过，不再赘述，唯一的区别是需要在结尾节点上标志当前模式串的长度。

public void insertStr(char[] chars) {
       //首先判断首字符是否已经在字典树中，然后判断第二字符，依次往下进行判断，找到第一个不存在的字符进行插入孩节点
       Node p = root;
       //表明当前处理到了第几个字符
       int chIndex = 0;
       while (chIndex < chars.length) {
           while (chIndex < chars.length && null != p) {
               Node[] children = p.childNode;
               boolean find = false;
               for (Node child : children) {
                   if (null == child) {continue;}
                   if (child.value == chars[chIndex]) {
                       //当前字符已经存在，不需要再进行存储
                       //从当前节点出发，存储下一个字符
                       p = child;
                       ++ chIndex;
                       find = true;
                       break;
                  }
              }
               if (Boolean.TRUE.equals(find)) {
                   //在孩子中找到了 不用再次存储
                   break;
              }
               //如果把孩子节点都找遍了，还没有找到这个字符，直接将这个字符加入当前节点的孩子节点
               Node node = new Node(chars[chIndex]);
               node.childNode = new Node[26];
               children[chars[chIndex] - 'a'] = node;
               p = node;
               ++ chIndex;
          }
      }
       //字符串中字符全部进入tire树中后，将最后一个字符所在节点标志为结尾节点
       p.isTail = true;
       p.tailLength = chars.length;
  }

构建失败指针

从根节点开始层序遍历树结构，构建失败指针。一个节点的子节点的失败指针可以根据当前节点的失败指针得到，因为我们是用后缀去与前缀匹配，所以如果我们采用层序遍历，与当前后缀的前缀一定在上层，已经匹配出来了。那么当前节点的子节点的失败指针则可以根据当前节点的失败指针，查找失败指针指向的节点的子节点是否有与当前节点的子节点相等的，相等则这个子节点的失败指针直接指向，不相等则继续找，找不到直接指向root。根据上面的图，我们来举一个例子，我们已经找到about中o节点（o1）的失败指针是out中的o节点（o2），接下来我们怎么找u（u1）的失败指针呢？首先根据o1的失败指针我们找到了o2，o2的子节点为u（u2），恰好与我们u1的值相等，此时我们就可以将u1的失败指针指向u2。以此类推，如果访问到最后为空（root的失败指针为空），则直接将失败指针指向root。

public void madeFailNext() {
       //层序遍历，为了保证求解这个节点失败指针的时候，它的父节点的失败指针以及失败指针的失败指针。。。。已经求得，可以完全根据这个找
       Deque<Node> nodes = new LinkedList<>();
       nodes.add(root);
       while (!nodes.isEmpty()) {
           Node current = nodes.poll();
           Node[] children = current.childNode;
           for (Node child : children) {
               if (null == child) {
                   continue;
              }
               Node failNode = current.failNode;
               while (null != failNode) {
                   //找到当前节点的失败指针，查看失败指针子节点是否有==
                   Node[] failChildren = failNode.childNode;
                   Node node = failChildren[child.value - 'a'];
                   if (null == node) {
                       //找当前指针的下一个指针
                       failNode = failNode.failNode;
                       continue;
                  }
                   //已经找到匹配的
                   //将失败指针指向node
                   child.failNode = node;
                   break;
              }
               //如果找完还没有找到，指向root
               if (null == failNode) {
                   child.failNode = root;
              }
               nodes.add(child);
          }
      }
  }

匹配

从首字符，字典树从root节点开始进行匹配，如果字符与节点值匹配，则判断是否为尾字符，如果是匹配上一个违禁词，记录下来，如果不匹配则转移到失败指针继续进行匹配。

/**
    * 匹配出str中所有出现的关键词
    * @param str
    * @return
    */
   public List<String> match(String str) {
       //遍历当前子串串，从根节点出发，如果匹配就一直往下进行匹配，同时需要看匹配的节点是否为结尾节点，如果是，匹配上一个
       //如果不匹配则通过失败指针转移到下一个节点
       this.dfs(root, 0, str);
       return machStr;
  }

   //abcdeasdabcebcd
   List<String> machStr = new ArrayList<>();
   private void dfs(Node node, int chIndex, String chars) {
       if (chIndex >= chars.length()) {
           return;
      }
       //从将当前字符与当前node的孩子节点进行匹配，如果当前字符与node的孩子节点.value匹配，判断当前字符是否为尾节点，是，则记录，匹配到了一个
       //继续匹配（子节点，与下一个元素进行匹配）
       //如果不匹配，则转到失败指针
       Node[] children = node.childNode;
       Node child = children[chars.charAt(chIndex) - 'a'];
       if (null == child) {
           //不匹配，转到失败指针
           //如果当前node==root，从root匹配，root的失败指针是null
           if (node == root) {
               dfs(root, ++ chIndex, chars);
          } else {
               dfs(node.failNode, chIndex, chars);
          }
      } else {
           //匹配到了
           if (child.isTail) {
               //并且是结尾节点，取从child.value到child.tailLength的字符
               machStr.add(chars.substring(chIndex - child.tailLength  + 1, chIndex + 1));
          }
           dfs(child, ++ chIndex, chars);
      }

  }

执行结果

public static void main(String[] args) {
       ACAutomaton acAutomaton = new ACAutomaton();
       //初始化一个仅有根节点的字典树
       acAutomaton.init();
       //构建Tire树
       acAutomaton.insertStr("out".toCharArray());
       acAutomaton.insertStr("about".toCharArray());
       acAutomaton.insertStr("act".toCharArray());
       //构建失败指针
       acAutomaton.madeFailNext();
       System.out.println("ces");
       //匹配
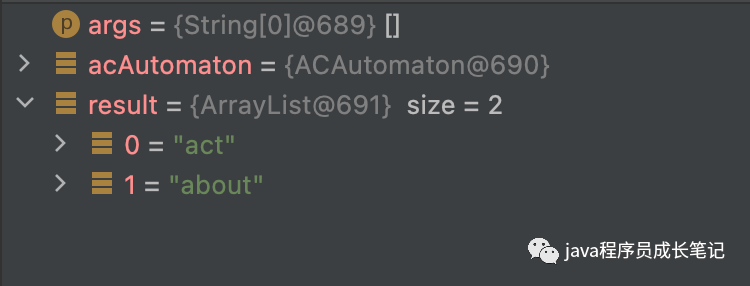
       List<String> result = acAutomaton.match("abcdeasactdaboutcebcd");
  }

到此这篇关于详解Java中AC自动机的原理与实现的文章就介绍到这了,更多相关Java AC自动机内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！