详解C++实现匈牙利算法

目录

• 一、匈牙利算法介绍
• 二、最大匹配问题
• 三、最小点覆盖问题
• 四、匈牙利算法的应用
• 4.1、（洛谷P1129） [ZJOI2007]矩阵游戏
• 4.2、（vijos1204） CoVH之柯南开锁
• 4.3、（TYVJ P1035） 棋盘覆盖

一、匈牙利算法介绍

匈牙利算法（Hungarian algorithm）主要用于解决一些与二分图匹配有关的问题，所以我们先来了解一下二分图。

二分图（Bipartite graph）是一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连。下图是典型的二分图。

可以看到，在上面的二分图中，每条边的端点都分别处于点集X和Y中。匈牙利算法主要用来解决两个问题：求二分图的最大匹配数和最小点覆盖数。

这么说起来过于抽象了，我们现在从实际问题出发。

二、最大匹配问题

看完上面讲的，相信读者会觉得云里雾里的：这是啥？这有啥用？所以我们把这张二分图稍微做点手脚，变成下面这样：

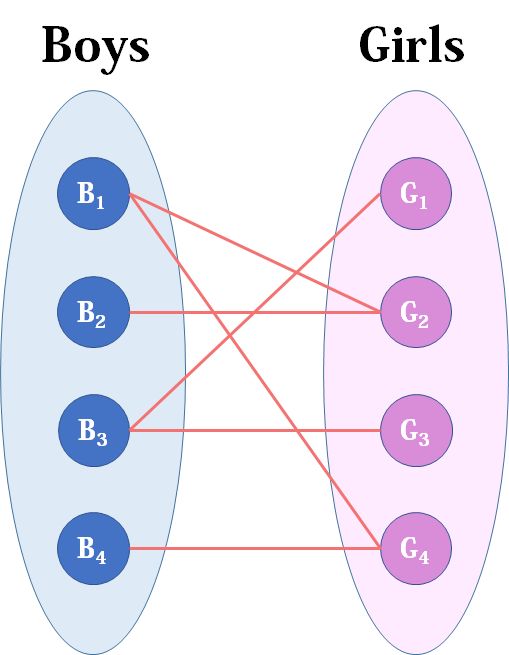
现在Boys和Girls分别是两个点集，里面的点分别是男生和女生，边表示他们之间存在“暧昧关系"。最大匹配问题相当于，假如你是红娘，可以撮合任何一对有暧昧关系的男女，那么你最多能成全多少对情侣？（数学表述：在二分图中最多能找到多少条没有公共端点的边）

现在我们来看看匈牙利算法是怎么运作的：

我们从B1看起（男女平等，从女生这边看起也是可以的），他与G2有暧昧，那我们就先暂时把他与G2连接（注意这时只是你作为一个红娘在纸上构想，你没有真正行动，此时的安排都是暂时的）。

来看B2，B2也喜欢G2，这时G2已经“名花有主”了（虽然只是我们设想的），那怎么办呢？我们倒回去看G2目前被安排的男友，是B1，B1有没有别的选项呢？有，G4，G4还没有被安排，那我们就给B1安排上G4。

然后B3，B3直接配上G1就好了，这没什么问题。至于B4，他只钟情于G4，G4目前配的是B1。B1除了G4还可以选G2，但是呢，如果B1选了G2，G2的原配B2就没得选了。我们绕了一大圈，发现B4只能注定单身了，可怜。（其实从来没被考虑过的G3更可怜）

这就是匈牙利算法的流程，至于具体实现，我们来看看代码：

int M, N;            //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN];         //记录当前右侧元素所对应的左侧元素
bool vis[MAXN];      //记录右侧元素是否已被访问过
bool match(int i)
{
    for (int j = 1; j <= N; ++j)
        if (Map[i][j] && !vis[j]) //有边且未访问
        {
            vis[j] = true;                 //记录状态为访问过
            if (p[j] == 0 || match(p[j])) //如果暂无匹配，或者原来匹配的左侧元素可以找到新的匹配
            {
                p[j] = i;    //当前左侧元素成为当前右侧元素的新匹配
                return true; //返回匹配成功
            }
        }
    return false; //循环结束，仍未找到匹配，返回匹配失败
}
int Hungarian()
{
    int cnt = 0;
    for (int i = 1; i <= M; ++i)
    {
        memset(vis, 0, sizeof(vis)); //重置vis数组
        if (match(i))
            cnt++;
    }
    return cnt;
}

其实流程跟我们上面描述的是一致的。注意这里使用了一个递归的技巧，我们不断往下递归，尝试寻找合适的匹配。

三、最小点覆盖问题

另外一个关于二分图的问题是求最小点覆盖：我们想找到最少的一些点，使二分图所有的边都至少有一个端点在这些点之中。倒过来说就是，删除包含这些点的边，可以删掉所有边。

这为什么用匈牙利算法可以解决呢？你如果以为我要长篇大论很久就错了，我们只需要一个定理：

（König定理）

一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

好了，本节可以结束了，我们不是搞数学的，不需要证明。但是提供一个直观地找最小覆盖点集的方法：看题图，从左侧一个未匹配成功的点出发，走一趟匈牙利算法的流程（即紫色的箭头），所有左侧未经过的点，和右侧经过的点，即组成最小点覆盖。（即图中的B3、G2、G4）

对于每个左部节点，寻找增广路最多遍历整张二分图一次，因此，该算法时间复杂度为O(MN)

四、匈牙利算法的应用

一些题目，乍一看与上面这个男女配对的问题没有任何相似点，其实都可以用匈牙利算法。例如：

4.1、（洛谷P1129） [ZJOI2007]矩阵游戏

题目描述

小Q是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个$ N× N $ 黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作：
行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色）
列交换操作：选择矩阵的任意两列，交换这两列（即交换对应格子的颜色）
游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。
对于某些关卡，小Q百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！于是小Q决定写一个程序来判断这些关卡是否有解。
输入格式
第一行包含一个整数T，表示数据的组数。
接下来包含T组数据，每组数据第一行为一个整数N，表示方阵的大小；接下来N行为一个 $ N× N $的01矩阵（0表示白色，1表示黑色）。
输出格式
包含T行。对于每一组数据，如果该关卡有解，输出一行Yes；否则输出一行No。

我们把矩阵转化为二分图（左侧集合代表各行，右侧集合代表各列，某位置为1则该行和该列之间有边）。我们想进行一系列交换操作，使得X1连上Y1，X2连上Y2，……

大家可以想象，所谓的交换，是不是可以等价为重命名？我们可以在保持当前二分图结构不变的情况下，把右侧点的编号进行改变，这与交换的效果是一样的。

所以想让X1、X2...与Y1、Y2...一一对应，其实只需要原图最大匹配数为4就行了。（这与组合数学中相异代表系的概念相合）。代码如下：

#include <cstdio>
#include <cstring>
int Map[205][205], p[205], vis[205], N, T;
bool match(int i){
    for (int j = 1; j <= N; ++j){
        if (Map[i][j] && !vis[j]){
            vis[j] = 1;
            if (p[j] == 0 || match(p[j])){
                p[j] = i;
                return true;
            }
        }
    }
    return false;
}
int Hungarian(){
    int cnt = 0;
    for (int i = 1; i <= N; ++i){
        memset(vis, 0, sizeof(vis));
        if (match(i))
            cnt++;
    }
    return cnt;
}
int main(){
    scanf("%d", &T);
    while (T--){
        scanf("%d", &N);
        memset(p, 0, sizeof(p));
        for (int i = 1; i <= N; ++i)
            for (int j = 1; j <= N; ++j)
                scanf("%d", &Map[i][j]);
        puts(Hungarian() == N ? "Yes" : "No");
    }
    return 0;
}

4.2、（vijos1204） CoVH之柯南开锁

面对OIBH组织的嚣张气焰, 柯南决定深入牛棚, 一探虚实.
他经过深思熟虑, 决定从OIBH组织大门进入...........
OIBH组织的大门有一个很神奇的锁.
锁是由M*N个格子组成, 其中某些格子凸起(灰色的格子). 每一次操作可以把某一行或某一列的格子给按下去.

如果柯南能在组织限定的次数内将所有格子都按下去, 那么他就能够进入总部. 但是OIBH组织不是吃素的, 他们的限定次数恰是最少次数.

请您帮助柯南计算出开给定的锁所需的最少次数.

读入/Input：

第一行 两个不超过100的正整数N, M表示矩阵的长和宽
以下N行 每行M个数 非0即1 1为凸起方格

输出/Output：

一个整数 所需最少次数

如果我们把样例的矩阵，转化为二分图的形式，是这样的：

按下一行或一列，其实就是删掉与某个点相连的所有边。现在要求最少的操作次数，想想看，这不就是求最小点覆盖数吗？所以直接套匈牙利算法即可。代码略。

4.3、（TYVJ P1035） 棋盘覆盖

描述 Description
给出一张nn(n<=100)的国际象棋棋盘，其中被删除了一些点，问可以使用多少12的多米诺骨牌进行掩盖。
输入格式 Input Format
第一行为n，m（表示有m个删除的格子）
第二行到m+1行为x,y，分别表示删除格子所在的位置
x为第x行
y为第y列
输出格式 Output Format
一个数，即最大覆盖格数

经典的多米诺覆盖问题大家都很熟悉，我们把棋盘染色，每个多米诺骨牌恰好覆盖一个白格和一个黑格（这里为了美观染成了其他颜色，下面仍将其称作黑格）。

我们删除了一些格子：

现在要求多米诺骨牌最大覆盖数。

你可能已经看出来了，我们在染色之后，黑格和白格可以构成一个二分图，每个白格都只和黑格相连，每个黑格也只和白格相连。在给所有黑格和白格编号后，我们把每个未删除的格子都与它上下左右紧邻的未删除的格子相连。很显然，这张二分图的最大匹配数，就是我们能放下最多的多米诺骨牌数。注意因为数据范围较大，要用邻接表存图。

#include <cstdio>
#include <cstring>
#define MAXN 5500
struct Edges
{
    int to, next;
} edges[MAXN * 8];
int Map[105][105], head[MAXN], p[MAXN], vis[MAXN], N, cnt_edge;
inline int add(int from, int to)
{
    edges[++cnt_edge].next = head[from];
    head[from] = cnt_edge;
    edges[cnt_edge].to = to;
}
inline int trans(int i, int j, int n) //把坐标转化为编号
{
    return ((i - 1) * n + j + 1) / 2;
}
bool match(int i)
{
    for (int e = head[i]; e; e = edges[e].next)
    {
        int j = edges[e].to;
        if (!vis[j])
        {
            vis[j] = true;
            if (p[j] == 0 || match(p[j]))
            {
                p[j] = i;
                return true;
            }
        }
    }
    return false;
}
int Hungarian()
{
    int cnt = 0;
    for (int i = 1; i <= N; ++i)
    {
        memset(vis, 0, sizeof(vis));
        if (match(i))
            cnt++;
    }
    return cnt;
}
int main()
{
    int n, m, x, y;
    scanf("%d%d", &n, &m);
    N = (n * n + 1) / 2;
    memset(Map, -1, sizeof(Map));
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j)
            Map[i][j] = 0;
    for (int i = 0; i < m; ++i)
    {
        scanf("%d%d", &x, &y);
        Map[x][y] = -1;
    }
    for (int i = 1; i <= n; i++)
        for (int j = i % 2 ? 1 : 2; j <= n; j += 2)
            if (Map[i][j] == 0)
            {
                if (Map[i + 1][j] != -1)
                    add(trans(i, j, n), trans(i + 1, j, n));
                if (Map[i][j + 1] != -1)
                    add(trans(i, j, n), trans(i, j + 1, n));
                if (Map[i - 1][j] != -1)
                    add(trans(i, j, n), trans(i - 1, j, n));
                if (Map[i][j - 1] != -1)
                    add(trans(i, j, n), trans(i, j - 1, n));
            }
    printf("%d\n", Hungarian());
    return 0;
}

以上就是详解C++实现匈牙利算法的详细内容，更多关于C++匈牙利算法的资料请关注我们其它相关文章！