Python遗传算法Geatpy工具箱使用介绍

目录

• 一、 什么是遗传算法？
• 二、 遗传算法库Geatpy
• 2.1 遗传算法工具箱Geatpy参数介绍
• 三、最佳实践
• 3.1 代码示例 | 参数模板
• 3.2 最佳实践

一、 什么是遗传算法？

遗传算法是仿真生物遗传学和自然选择机理，通过人工方式所构造的一类搜索算法，从某种程度上说遗传算法是对生物进化过程进行的数学方式仿真。生物种群的生存过程普遍遵循达尔文进化准则，群体中的个体根据对环境的适应能力而被大自然所选择或淘汰。进化过程的结果反映在个体的结构上，其染色体包含若干基因，相应的表现型和基因型的联系体现了个体的外部特性与内部机理间逻辑关系。通过个体之间的交叉、变异来适应大自然环境。生物染色体用数学方式或计算机方式来体现就是一串数码，仍叫染色体，有时也叫个体；适应能力是对应着一个染色体的一个数值来衡量；染色体的选择或淘汰则按所面对的问题是求最大还是最小来进行。

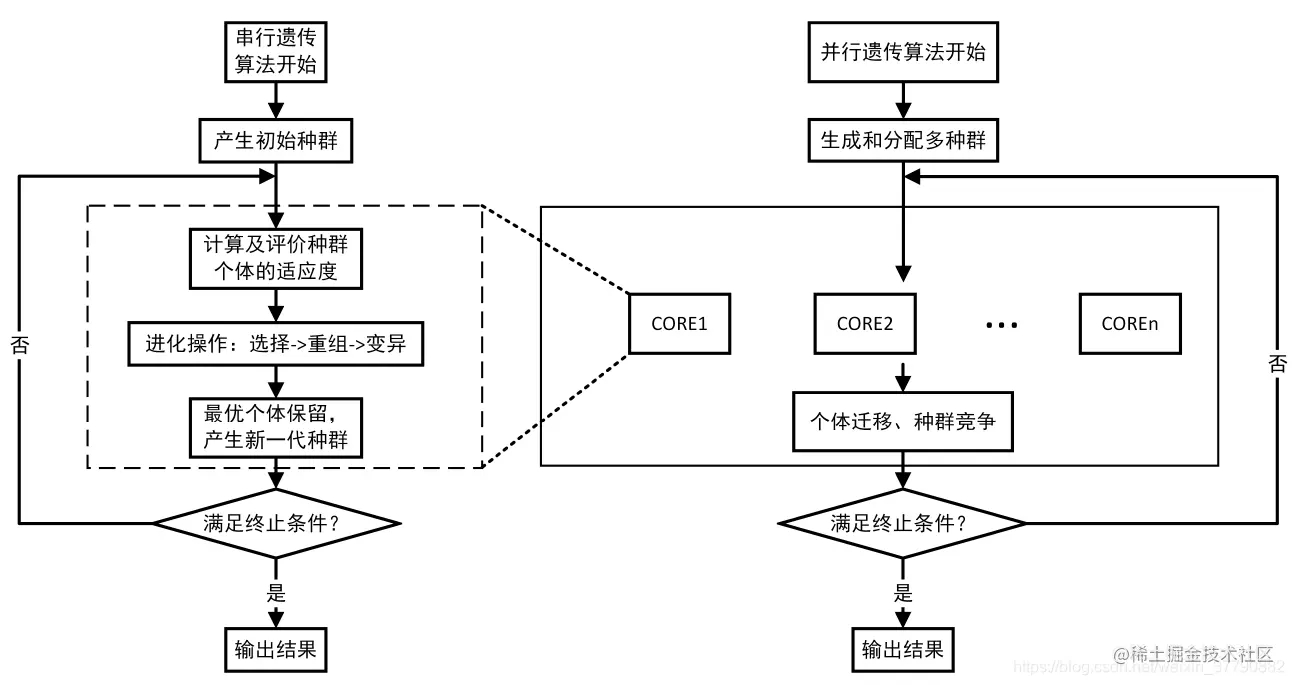
二、 遗传算法库Geatpy

2.1 遗传算法工具箱Geatpy参数介绍

API官方参考文档

population参数【重要属性：Chrom，Phen，Objv，CV，FitnV】

• sizes : int - 种群规模，即种群的个体数目。
• ChromNum : int - 染色体的数目，即每个个体有多少条染色体。
• Encoding : str - 染色体编码方式， 'BG':二进制/格雷编码； 'RI':实整数编码，即实数和整数的混合编码； 'P':排列编码
• Field : array - 译码矩阵
• Chrom : array - 种群染色体矩阵，每一行对应一个个体的一条染色体。
• Lind : int - 种群染色体长度。
• ObjV : array - 种群目标函数值矩阵，每一行对应一个个体的目标函数值，每一列对应一个目标
• FitnV : array - 种群个体适应度列向量，每个元素对应一个个体的适应度，最小适应度为0
• CV : array - CV(Constraint Violation Value)是用来定量描述违反约束条件程度的矩阵，每行对应一个个体，每列对应一个约束
• Phen : array - 种群表现型矩阵（即种群各染色体解码后所代表的决策变量所组成的矩阵）。
• 如果通过CV矩阵基于可行性法则进行约束的设置，那么 不等式约束需要 ≤，等式约束 需要传入abs( ) (因为遵循值越大，适应度越小的原则)

• ea.Problem.init()中的lbin与ubin（决策变量范围边界矩阵）表示范围区间的开闭，1闭合0开区间

Geatpy 结果参数介绍

success: True or False, 表示算法是否成功求解。

stopMsg: 存储着算法停止原因的字符串。

optPop: 存储着算法求解结果的种群对象。如果无可行解，则optPop.sizes=0。optPop.Phen为决策变量矩阵，optPop.ObjV为目标函数值矩阵。

lastPop: 算法进化结束后的最后一代种群对象。

Vars: 等于optPop.Phen，此处即最优解。若无可行解，则Vars=None。

ObjV: 等于optPop.ObjV，此处即最优解对应的目标函数值。若无可行解，ObjV=None。

CV: 等于optPop.CV，此处即最优解对应的违反约束程度矩阵。若无可行解，CV=None。

startTime: 程序执行开始时间。

endTime: 程序执行结束时间。

executeTime: 算法 所用时间。

nfev: 算法评价次数

gd: (多目标优化且给定了理论最优解时才有) GD指标值。

igd: (多目标优化且给定了理论最优解时才有) IGD指标值。

hv: (多目标优化才有) HV指标值。

spacing: (多目标优化才有) Spacing指标值。

三、最佳实践

3.1 代码示例 | 参数模板

解集：

header_regex = '|'.join(['{}'] * len(headers))
header_str = header_regex.format(*[str(key).center(width) for key, width in zip(headers, widths)])
print("=" * len(header_str))
            print(header_str)
            print("-" * len(header_str))

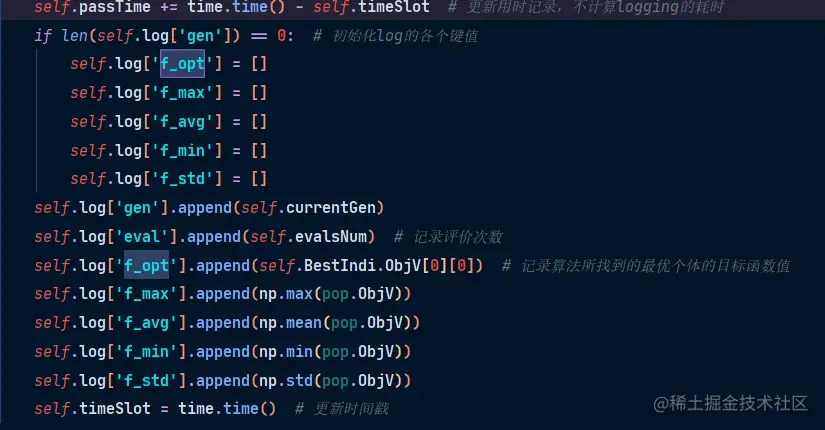
gen: 进化代数      
eval:记录评价次数        
f\_opt: 当代最优个体的目标函数值           
f\_max=当代种群最大函数值          
f\_min 最小   f\_avg ： 平均水平          
f\_std: 标准约束水平

3.2 最佳实践

使用geatpy库求解有向无环图最短路

代码【最短路】一：使用geatpy库

import numpy as np
import geatpy as ea
class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'Shortest_Path'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 10  # 初始化Dim（决策变量维数）
        varTypes = [1] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [0] * Dim  # 决策变量下界
        ub = [9] * Dim  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界 1表示闭合区间，0表示开区间
        ubin = [1] * Dim  # 决策变量上边界
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
        # 设置每一个结点下一步可达的结点（结点从1开始数，因此列表nodes的第0号元素设为空列表表示无意义）
        self.nodes = [[], [2, 3], [3, 4, 5], [5, 6], [7, 8], [4, 6], [7, 9], [8, 9], [9, 10], [10]]
        # 设置有向图中各条边的权重
        self.weights = {'(1, 2)': 36, '(1, 3)': 27, '(2, 4)': 18, '(2, 5)': 20, '(2, 3)': 13, '(3, 5)': 12,
                        '(3, 6)': 23,
                        '(4, 7)': 11, '(4, 8)': 32, '(5, 4)': 16, '(5, 6)': 30, '(6, 7)': 12, '(6, 9)': 38,
                        '(7, 8)': 20,
                        '(7, 9)': 32, '(8, 9)': 15, '(8, 10)': 24, '(9, 10)': 13}
    def decode(self, priority):  # 将优先级编码的染色体解码得到一条从节点1到节点10的可行路径
        edges = []  # 存储边
        path = [1]  # 结点1是路径起点
        while not path[-1] == 10:  # 开始从起点走到终点
            currentNode = path[-1]  # 得到当前所在的结点编号
            nextNodes = self.nodes[currentNode]  # 获取下一步可达的结点组成的列表
            chooseNode = nextNodes[np.argmax(
                priority[np.array(nextNodes) - 1])]  # 从NextNodes中选择优先级更高的结点作为下一步要访问的结点，因为结点从1数起，而下标从0数起，因此要减去1
            path.append(chooseNode)
            edges.append((currentNode, chooseNode))
        return path, edges
    def aimFunc(self, pop):  # 目标函数
        pop.ObjV = np.zeros((pop.sizes, 1))  # 初始化ObjV
        for i in range(pop.sizes):  # 遍历种群的每个个体，分别计算各个个体的目标函数值
            priority = pop.Phen[i, :]
            path, edges = self.decode(priority)  # 将优先级编码的染色体解码得到访问路径及经过的边
            pathLen = 0
            for edge in edges:
                key = str(edge)  # 根据路径得到键值，以便根据键值找到路径对应的长度
                if not key in self.weights:
                    raise RuntimeError("Error in aimFunc: The path is invalid. (当前路径是无效的。)", path)
                pathLen += self.weights[key]  # 将该段路径长度加入
            pop.ObjV[i] = pathLen  # 计算目标函数值，赋值给pop种群对象的ObjV属性
## 执行脚本
if __name__ == "__main__":
    # 实例化问题对象
    problem = MyProblem()
    # 构建算法
    algorithm = ea.soea_EGA_templet(problem,
                                    ea.Population(Encoding='RI', NIND=4),
                                    MAXGEN=10,  # 最大进化代数
                                    logTras=1)  # 表示每隔多少代记录一次日志信息
    # 求解
    res = ea.optimize(algorithm, verbose=True, drawing=1, outputMsg=False, drawLog=False, saveFlag=True,
                      dirName='result')
    print('最短路程为：%s' % (res['ObjV'][0][0]))
    print('最佳路线为：')
    best_journey, edges = problem.decode(res['Vars'][0])
    for i in range(len(best_journey)):
        print(int(best_journey[i]), end=' ')
    print()

以上就是Python遗传算法Geatpy工具箱使用介绍的详细内容，更多关于Python遗传算法Geatpy的资料请关注我们其它相关文章！