笛卡尔乘积介绍

笛卡尔（Descartes）乘积又叫直积。假设集合A={a,b}，集合B={0,1,2}，则两个集合的笛卡尔积为{(a,0),(a,1),(a,2),(b,0),(b,1), (b,2)}。可以扩展到多个集合的情况。类似的例子有，如果A表示某学校学生的集合，B表示该学校所有课程的集合，则A与B的笛卡尔积表示所有可能的选课情况。

在数学中，两个集合 X 和 Y 的笛卡儿积（Cartesian product），又称直积，表示为 X × Y，是其第一个对象是 X 的成员而第二个对象是 Y 的一个成员的所有可能的有序对：

。

笛卡儿积得名于笛卡儿，他的解析几何的公式化引发了这个概念。

具体的说，如果集合 X 是 13 个元素的点数集合 { A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2 } 而集合 Y 是 4 个元素的花色集合 {♠, ♥, ♦, ♣}，则这两个集合的笛卡儿积是 52 个元素的标准扑克牌的集合 { (A, ♠), (K, ♠), ..., (2, ♠), (A, ♥), ..., (3, ♣), (2, ♣) }。

目录

  • 1 笛卡儿积的性质
  • 2 笛卡儿平方和 n-元乘积
  • 3 无穷乘积
  • 4 函数的笛卡儿积
  • 5 外部链接
  • 6 参见 笛卡儿积的性质

易见笛卡儿积满足下列性质：

  • 对于任意集合 A，根据定义有 
  • 一般来说笛卡儿积不满足交换律和结合律。
  • 笛卡儿积对集合的并和交满足分配律，即








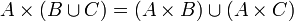
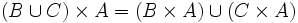
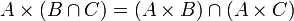
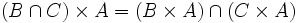
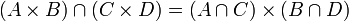
笛卡儿平方和 n-元乘积

集合 X 的笛卡儿平方(或二元笛卡儿积)是笛卡儿积 X × X。一个例子是二维平面 R × R，这里 R 是实数的集合 - 所有的点 (x,y)，这里的 x 和 y 是实数(参见笛卡儿坐标系)。

可以推广出在 n 个集合 X1, ..., Xn 上的 n-元笛卡儿积:

。

实际上，它可以被认同为 (X1 × ... × Xn-1) × Xn。它也是 n-元组的集合。

一个例子是欧几里得三维空间 R × R × R，这里的 R 再次是实数的集合。

为了辅助它的计算，可绘制一个表格。一个集合作为行而另一个集合作为列，从行和列的集合选择元素形成有序对作为表的单元格。

无穷乘积

对最常用的数学应用而言上述定义通常就是所需要的全部。但是有可能在任意(可能无限)的集合的搜集上定义笛卡儿积。如果 I 是任何指标集合，而

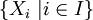
是由 I 索引的集合的搜集，则我们定义

，

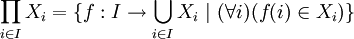就是定义在索引集合上的所有函数的集合，使得这些函数在特定索引 i 上的值是 Xi  的元素。

对在 I 中每个 j，定义自

的函数

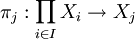
叫做第 j 投影映射。

n-元组可以被看作在 {1, 2, ..., n} 上的函数，它在 i 上的值是这个元组的第 i 个元素。所以，在 I 是 {1, 2, ..., n} 的时候这个定义一致于对有限情况的定义。在无限情况下这个定义是集合族。

特别熟悉的一个无限情况是在索引集合是自然数的集合  的时候: 这正是其中第 i 项对应于集合 Xi  的所有无限序列的集合。再次， 提供了这样的一个例子:

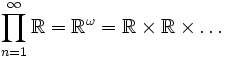
是实数的无限序列的搜集，并且很容易可视化为带有有限数目构件的向量或元组。另一个特殊情况(上述例子也满足它)是在乘积涉及因子 Xi 都是相同的时候，类似于“笛卡儿指数”。则在定义中的无限并集自身就是这个集合自身，而其他条件被平凡的满足了，所以这正是从 I 到 X 的所有函数的集合。

此外，无限笛卡儿积更少直觉性，尽管有应用于高级数学的价值。

断言非空集合的任意非空搜集的笛卡儿积为非空等价于选择公理。

函数的笛卡儿积

如果 f 是从 A 到 B 的函数而 g 是从 X 到 Y 的函数，则它们的笛卡儿积 f×g 是从 A×X 到 B×Y 的函数，带有

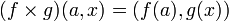
上述可以被扩展到函数的元组和无限指标。

赞 (0)

相关推荐

  • 基于JS实现的笛卡尔乘积之商品发布

    基于JS实现的笛卡尔乘积之商品发布

    没给大家介绍正文之前先给大家补充点知识: js笛卡尔积算法 根据给的对象或者数组生成笛卡尔积 //笛卡儿积组合 function descartes(list) { //parent上一级索引;count指针计数 var point = {}; var result = []; var pIndex = null; var tempCount = 0; var temp = []; //根据参数列生成指针对象 for(var index in list) { if(typeof list[ind

  • JS实现简单的二维矩阵乘积运算

    JS实现简单的二维矩阵乘积运算

    本文实例讲述了JS实现简单的二维矩阵乘积运算方法.分享给大家供大家参考,具体如下: Console控制台截图如下: (上图为输出结果直接上代码了(A矩阵可以乘以B矩阵的前提是A矩阵的列数等于B矩阵的行数) <!DOCTYPE html> <html> <head> <title>demo</title> </head> <body> </body> <script type="text/java

  • javascript笛卡尔积算法实现方法

    本文实例讲述了javascript笛卡尔积算法实现方法.分享给大家供大家参考.具体分析如下: 这里可根据给的对象或者数组生成笛卡尔积 //笛卡儿积组合 function descartes(list) { //parent上一级索引;count指针计数 var point = {}; var result = []; var pIndex = null; var tempCount = 0; var temp = []; //根据参数列生成指针对象 for(var index in list)

  • .net C# 实现任意List的笛卡尔乘积算法代码

    可以扩展到多个集合的情况.类似的例子有,如果A表示某学校学生的集合,B表示该学校所有课程的集合,则A与B的笛卡尔积表示所有可能的选课情况 复制代码 代码如下: using System;using System.Collections.Generic;using System.Diagnostics;using System.Linq; namespace 算法{    public static class 算法    {        /// <summary>        /// 笛卡

  • Javascript浮点数乘积运算出现多位小数的解决方法

    Javascript在进行浮点数的乘积运算,会出现多位小数的情况. 这是由于在运算的时候先把浮点数转化成二进制后进行运算,但是有的小数在二进制编码后出现无限循环,因而导致计算出现了误差,在其它变成语言中也有类似的问题. 原因解释参考自百度知道: 例如:求1038.1-1000 1038.1=10000001110.0001100110011001100110011001100110011001100..... 1000 =1111101000 1038.1转化为二进制是个无限循环小数,1100是

  • 笛卡尔乘积介绍

    笛卡尔乘积介绍

    笛卡尔(Descartes)乘积又叫直积.假设集合A={a,b},集合B={0,1,2},则两个集合的笛卡尔积为{(a,0),(a,1),(a,2),(b,0),(b,1), (b,2)}.可以扩展到多个集合的情况.类似的例子有,如果A表示某学校学生的集合,B表示该学校所有课程的集合,则A与B的笛卡尔积表示所有可能的选课情况. 在数学中,两个集合 X 和 Y 的笛卡儿积(Cartesian product),又称直积,表示为 X × Y,是其第一个对象是 X 的成员而第二个对象是 Y 的一个成员

  • Python实现求笛卡尔乘积的方法

    Python实现求笛卡尔乘积的方法

    本文实例讲述了Python实现求笛卡尔乘积的方法.分享给大家供大家参考,具体如下: 在数学中,两个集合X和Y的笛卡尓乘积(Cartesian product),又称直积,表示为X × Y,第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员.假设集合A={a,b},集合B={0,1,2},则两个集合的笛卡尔积为{(a,0), (a,1), (a,2), (b,0), (b,1), (b, 2)}.有时我们需要在python求两个list的笛卡尔乘积,其实很简单,一行代码搞定. 例如

  • 利用python绘制笛卡尔直角坐标系

    利用python绘制笛卡尔直角坐标系

    背景: 有些数学题目经常要用到数形结合思想,尤其是一些函数题目,如果能够把函数图像画出来进行解题的话,思路会更加清晰明了.python绘图主要用到matplotlib绘图模块,平时我们看到的往往是下面这种图 用一个实线矩形把几何图形封闭起来,看起来好像在一个象限里面.现实中,我们通常采用描点作图,首先建立一个笛卡尔直角坐标系,然后根据一个自变量,一个因变量的在坐标系里面描一些点,然后用一条光滑曲线把这些点串起来,更像下面这种图 那么,我们怎么才能利用matplotlib模块画出上面的正弦函数呢?

  • Python简单实现两个任意字符串乘积的方法示例

    本文实例讲述了Python简单实现两个任意字符串乘积的方法.分享给大家供大家参考,具体如下: 题目: 给定两个任意数字组成的字符串,求乘积,字符可能很大,但是python具有无限精度的整数在这里就不需要考虑这个问题了 下面是简单的实现: #!usr/bin/env python #encoding:utf-8 ''''' __Author__:沂水寒城 功能:两个任意字符串乘积 ''' def two_strs_mutiply(one_str, two_str): ''''' ''' if on

  • Python编程语言的35个与众不同之处（语言特征和使用技巧）

    一.Python介绍 从我开始学习Python时我就决定维护一个经常使用的"窍门"列表.不论何时当我看到一段让我觉得"酷,这样也行!"的代码时(在一个例子中.在StackOverflow.在开源码软件中,等等),我会尝试它直到理解它,然后把它添加到列表中.这篇文章是清理过列表的一部分.如果你是一个有经验的Python程序员,尽管你可能已经知道一些,但你仍能发现一些你不知道的.如果你是一个正在学习Python的C.C++或Java程序员,或者刚开始学习编程,那么你会像

  • MySQL中union和join语句使用区别的辨析教程

    MySQL中union和join语句使用区别的辨析教程

    union和join是需要联合多张表时常见的关联词,具体概念我就不说了,想知道上网查就行,因为我也记不准确. 先说差别:union对两张表的操作是合并数据条数,等于是纵向的,要求是两张表字段必须是相同的(Schema of both sides of union should match.).也就是说如果A表中有三条数据,B表中有两条数据,那么A union B就会有五条数据.说明一下union 和union all的差别,对于union如果存在相同的数据记录会被合并,而union all不会合

  • Python 迭代器工具包【推荐】

    原文:https://git.io/pytips 0x01 介绍了迭代器的概念,即定义了 __iter__() 和 __next__() 方法的对象,或者通过 yield 简化定义的"可迭代对象",而在一些函数式编程语言(见 0x02 Python 中的函数式编程)中,类似的迭代器常被用于产生特定格式的列表(或序列),这时的迭代器更像是一种数据结构而非函数(当然在一些函数式编程语言中,这两者并无本质差异).Python 借鉴了 APL, Haskell, and SML 中的某些迭代器

  • 五种提高 SQL 性能的方法

    五种提高 SQL 性能的方法

    发布日期: 4/1/2004 | 更新日期: 4/1/2004 Johnny Papa Data Points Archive 有时, 为了让应用程序运行得更快,所做的全部工作就是在这里或那里做一些很小调整.啊,但关键在于确定如何进行调整!迟早您会遇到这种情况:应用程序中的 SQL 查询不能按照您想要的方式进行响应.它要么不返回数据,要么耗费的时间长得出奇.如果它降低了报告或您的企业应用程序的速度,用户必须等待的时间过长,他们就会很不满意.就像您的父母不想听您解释为什么在深更半夜才回来一样,用户

随机推荐