python实现梯度法 python最速下降法

假设我们已经知道梯度法——最速下降法的原理。

现给出一个算例：

如果人工直接求解：

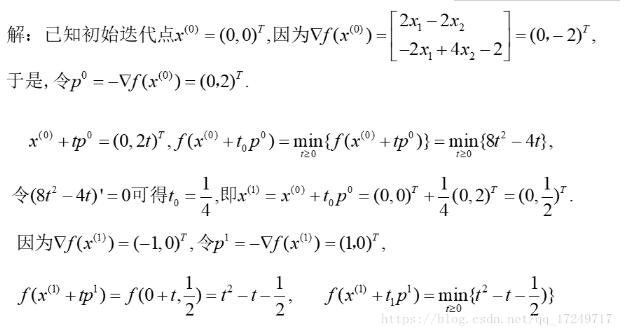
现给出Python求解过程：

import numpy as np
from sympy import *
import math
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist

# 定义符号
x1, x2, t = symbols('x1, x2, t')

def func():
 # 自定义一个函数
 return pow(x1, 2) + 2 * pow(x2, 2) - 2 * x1 * x2 - 2 * x2

def grad(data):
 # 求梯度向量,data=[data1, data2]
 f = func()
 grad_vec = [diff(f, x1), diff(f, x2)] # 求偏导数,梯度向量
 grad = []
 for item in grad_vec:
  grad.append(item.subs(x1, data[0]).subs(x2, data[1]))
 return grad

def grad_len(grad):
 # 梯度向量的模长
 vec_len = math.sqrt(pow(grad[0], 2) + pow(grad[1], 2))
 return vec_len

def zhudian(f):
 # 求得min(t)的驻点
 t_diff = diff(f)
 t_min = solve(t_diff)
 return t_min

def main(X0, theta):
 f = func()
 grad_vec = grad(X0)
 grad_length = grad_len(grad_vec) # 梯度向量的模长
 k = 0
 data_x = [0]
 data_y = [0]
 while grad_length > theta: # 迭代的终止条件
  k += 1
  p = -np.array(grad_vec)
  # 迭代
  X = np.array(X0) + t*p
  t_func = f.subs(x1, X[0]).subs(x2, X[1])
  t_min = zhudian(t_func)
  X0 = np.array(X0) + t_min*p
  grad_vec = grad(X0)
  grad_length = grad_len(grad_vec)
  print('grad_length', grad_length)
  print('坐标', X0[0], X0[1])
  data_x.append(X0[0])
  data_y.append(X0[1])

 print(k)

 # 绘图
 fig = plt.figure()
 ax = axisartist.Subplot(fig, 111)
 fig.add_axes(ax)
 ax.axis["bottom"].set_axisline_style("-|>", size=1.5)
 ax.axis["left"].set_axisline_style("->", size=1.5)
 ax.axis["top"].set_visible(False)
 ax.axis["right"].set_visible(False)
 plt.title(r'$Gradient \ method - steepest \ descent \ method$')
 plt.plot(data_x, data_y, label=r'$f(x_1,x_2)=x_1^2+2 \cdot x_2^2-2 \cdot x_1 \cdot x_2-2 \cdot x_2$')
 plt.legend()
 plt.scatter(1, 1, marker=(5, 1), c=5, s=1000)
 plt.grid()
 plt.xlabel(r'$x_1$', fontsize=20)
 plt.ylabel(r'$x_2$', fontsize=20)
 plt.show()

if __name__ == '__main__':
 # 给定初始迭代点和阈值
 main([0, 0], 0.00001)

最终结果图如下所示：

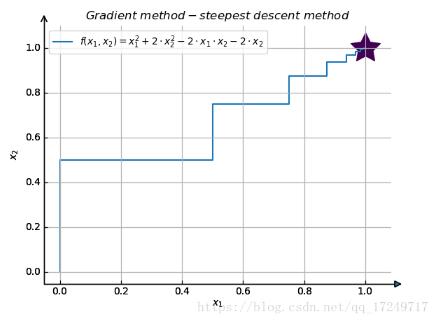
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。