Java数据结构二叉树难点解析

前言

本章，我们主要需要了解以下内容

• 什么是线索二叉树
• 怎么去把二叉树线索化
• 怎么通过线索二叉树查找某个数的后继结点
• 二叉树的查看——二叉树怎们遍历

什么是线索二叉树

首先我们来了解一下什么是线索二叉树？

定义：一个二叉树通过如下的方法“穿起来”：所有原本为空的右(孩子)指针改为指向该节点在中序序列中的后继，所有原本为空的左(孩子)指针改为指向该节点的中序序列的前驱。

再看一下为什么要有线索二叉树？

顾名思义，线索二叉树，肯定是根据线索查找，查找速度肯定更快。

• 线索二叉树能线性地遍历二叉树，从而比递归的中序遍历更快。使用线索二叉树也能够方便的找到一个节点的父节点，这比显式地使用父亲节点指针或者栈效率更高。这在栈空间有限，或者无法使用存储父节点的栈时很有作用（对于通过深度优先搜索来查找父节点而言)。

那线索仅仅是这样吗？当然不，我们都是懒的，能等待解决的问题，为什么会去想新的办法。我们要解决的是:

• 为了解决无法直接找到该结点在某种遍历序列中的前驱和后继结点的问题
• 但是同时出现了二叉链表找左、右孩子困难的问题，即在构建线索二叉树之后，链表的原来遍历方式会出问题。

最后看一下什么线索二叉树的图解

在我们的线索二叉树的书上，基本上都有以下这张图：

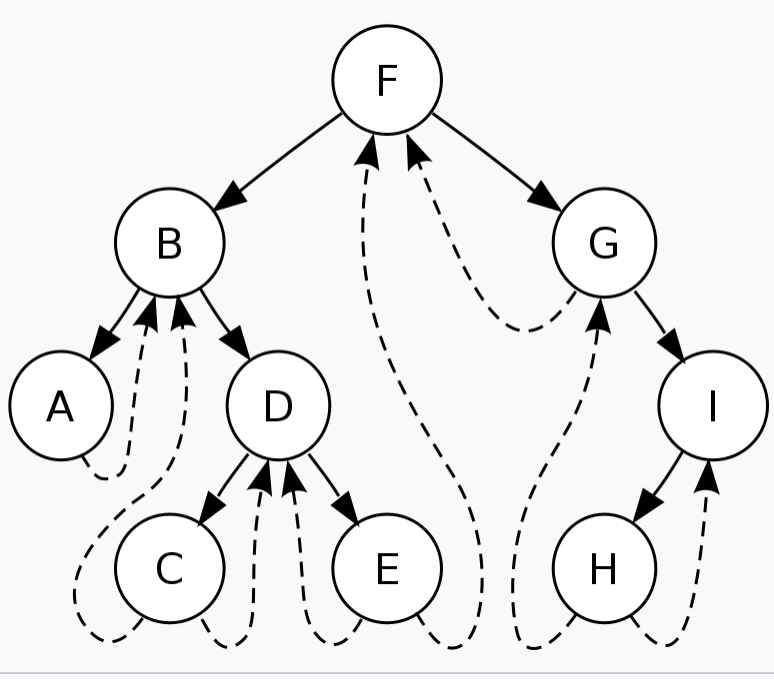
大家看到上面这张图还是有点懵的叭，我们一起看一下我下面手画的图

怎么去把二叉树线索化

哦！在着之前献给大家提一下，二叉树的遍历方式，有这样的几种

• 前序遍历二叉树的递归定义(根左右)
• 中序遍历二叉树的递归定义(左根右)
• 后续遍历二叉树的递归意义(左右根)

本博文主要讨论的是中序遍历
它的中序遍历结果就是ABCDE F GHI

它的中序线索二叉树遍历如下

先画线索二叉树

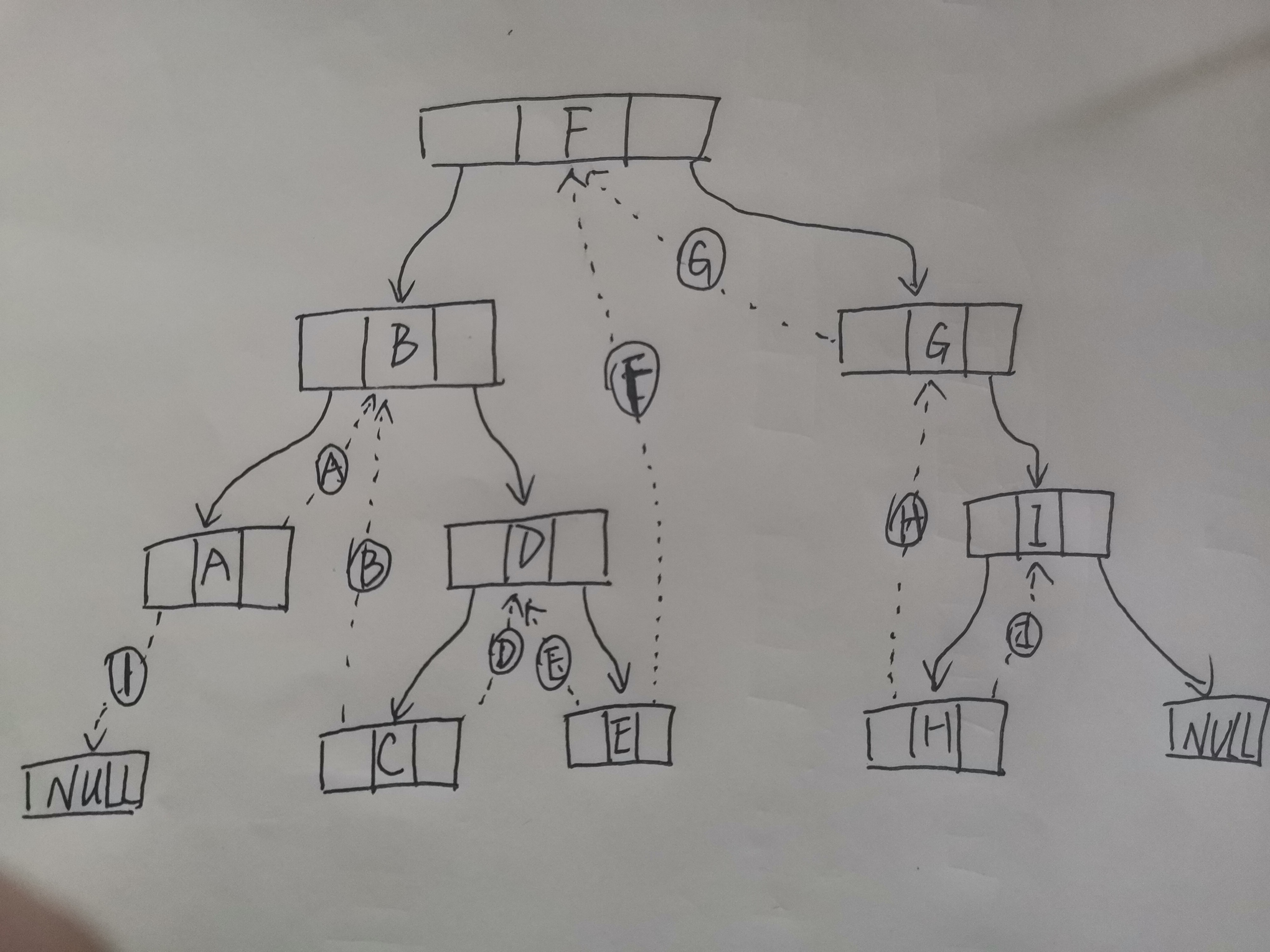
虚线箭头为线索指针，对于所有左指针指向空的节点：将该节点的左指针指向该节点在中序遍历中的上一节点；对于所有右指针指向空的节点，将该节点的右指针指向该节点在中序遍历中的下一结点。最后一个末尾结点除外。
中序图解线索二叉树

怎么通过线索二叉树查找某个数的后继结点

即形成了一个特殊的双向链表，之所以特殊，以F–>E为例，F–>E并不是直接到达，而是通过F–>B–>D–>E间接到达。

我们尝试用Java去构建一颗线索二叉树叭

先申明，我从未使用Java构建过树，二叉树都没有，若有错误，请指出

数据结点类

package com.testtree;

/**
 * @author pier
 */
public class TreeNode {
    /**数据域**/
    private int data;
    /**左指针**/
    private TreeNode left;
    /** 左孩子是否为线索，采用布尔类型主要是判断是否未null足以**/
    private boolean leftIsThread;
    /**右指针**/
    private TreeNode right;
    /** 右孩子是否为线索**/
    private boolean rightIsThread;

    /**根据数据域来确定所在的指针对应位置**/
    public TreeNode(int data)
    {
        this.data = data;
        this.left = null;
        this.leftIsThread = false;
        this.right = null;
        this.rightIsThread = false;
    }

    public int getData()
    {
        return data;
    }

    public void setData(int data)
    {
        this.data = data;
    }

    public TreeNode getLeft()
    {
        return left;
    }

    public void setLeft(TreeNode left)
    {
        this.left = left;
    }

    public boolean isLeftIsThread()
    {
        return leftIsThread;
    }

    public void setLeftIsThread(boolean leftIsThread)
    {
        this.leftIsThread = leftIsThread;
    }

    public TreeNode getRight()
    {
        return right;
    }

    public void setRight(TreeNode right)
    {
        this.right = right;
    }

    public boolean isRightIsThread()
    {
        return rightIsThread;
    }

    public void setRightIsThread(boolean rightIsThread)
    {
        this.rightIsThread = rightIsThread;
    }

    @Override
    public boolean equals(Object obj)
    {
        if (obj instanceof TreeNode )
        {
            TreeNode temp = (TreeNode) obj;
            if (temp.getData() == this.data)
            {
                return true;
            }
        }
        return false;
    }

    @Override
    public int hashCode()
    {
        return super.hashCode() + this.data;
    }
}

二叉树类

package com.testtree;
/*author:pier
2021/10/12
*/

public class BiTree {
    /** 根节点 **/
    private TreeNode root;
    /** 大小 **/
    private int size;
    /** 线索化的时候保存前驱 **/
    private TreeNode pre = null;

    public BiTree()
    {
        this.root = null;
        this.size = 0;
        this.pre = null;
    }

    public BiTree(int[] data)
    {
        this.pre = null;
        this.size = data.length;
        // 创建二叉树
        this.root = createTree(data, 1);
    }

    /**
     * 创建二叉树
     *
     */
    public TreeNode createTree(int[] data, int index)
    {
        if (index > data.length)
        {
            return null;
        }
        TreeNode node = new TreeNode(data[index - 1]);
        TreeNode left = createTree(data, 2 * index);
        TreeNode right = createTree(data, 2 * index + 1);
        node.setLeft(left);
        node.setRight(right);
        return node;
    }
    /**中序遍历**/
    public void inList(TreeNode root)
    {
        if (root != null)
        {
            inList(root.getLeft());
            System.out.print(root.getData() + ",");
            inList(root.getRight());
        }
    }

    public TreeNode getRoot()
    {
        return root;
    }

    public void setRoot(TreeNode root)
    {
        this.root = root;
    }

    public int getSize()
    {
        return size;
    }

    public void setSize(int size)
    {
        this.size = size;
    }
    /**线索化二叉树**/
    public void inThread(TreeNode root) {
        if ( root != null ) {
            // 线索化左孩子
            inThread(root.getLeft());
            // 左孩子为空
            if ( null == root.getLeft() )
            {
                // 将左孩子设置为线索
                root.setLeftIsThread(true);
                root.setLeft(pre);
            }
            // 右孩子为空
            if ( pre != null && null == pre.getRight() )
            {
                pre.setRightIsThread(true);
                pre.setRight(root);
            }
            pre = root;
            // 线索化右孩子
            inThread(root.getRight());
        }
    }
    /**
     * 中序遍历线索二叉树
     *
     */
    public void inThreadList(TreeNode root)
    {
        if (root != null)
        {
            // 如果左孩子不是线索
            while (root != null && !root.isLeftIsThread())
            {
                root = root.getLeft();
            }

            do
            {
                // 如果右孩子是线索
                System.out.print(root.getData() + ",");
                if (root.isRightIsThread())
                {
                    root = root.getRight();
                }
                // 有右孩子
                else
                {
                    root = root.getRight();
                    while (root != null && !root.isLeftIsThread())
                    {
                        root = root.getLeft();
                    }
                }
            } while (root != null);
        }
    }
}

测试类

package com.testtree;

/**
 * @author pier
 */
public class Test {
    public static void main(String[] args) {
    //不要问我为什么设置这么大，结尾看我效果截图
        int[] arr = new int[10000];
        for (int i = 0; i < arr.length; i++) {
            arr[i]=i+1;
        }
        //创建一颗二叉树
        BiTree biTree = new BiTree(arr);
        //中序遍历二叉树
        System.out.println("中序遍历结果如下:");
        long start1 = System.currentTimeMillis();
        biTree.inList(biTree.getRoot());
        long end1 = System.currentTimeMillis();
        System.out.println();
        System.out.println("普通遍历时间为:"+(end1-start1)+"毫秒");
        System.out.println("\n");
        //中序遍历将二叉树线索化
        biTree.inThread(biTree.getRoot());
        System.out.println("线索二叉树中序遍历如下:");
        long start2 = System.currentTimeMillis();
        biTree.inThreadList(biTree.getRoot());
        long end2 = System.currentTimeMillis();
        System.out.println();
        System.out.println("线索二叉树的遍历时间为:"+(end2-start2)+"毫秒");

    }
}

运行结果

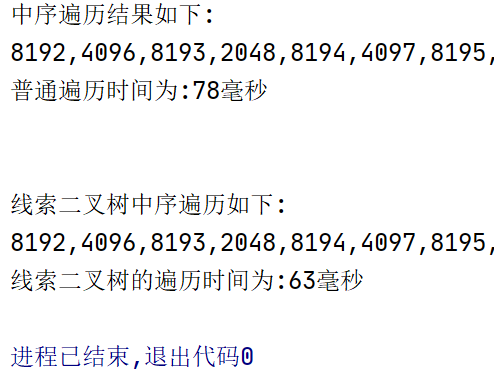
当我使用1-10的时候效果截图

完全看不出来差距，所以，哈哈才设置那么大，能够实践出来线索二叉树的遍历速度确实更快的。

Ps：看完这篇文章，你不来点个赞吗？不来个三连吗？重点是，你今天Get到了吗？别之后ALT+Insert自动生成get哟，用你那看起来不聪明的小脑袋瓜想一想。

到此这篇关于Java数据结构二叉树难点解析的文章就介绍到这了,更多相关Java 二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！