浅谈Python3实现两个矩形的交并比(IoU)

一、前言

因为最近刚好被问到这个问题，但是自己当时特别懵逼，导致没有做出来。所以下来后自己Google了很多IoU的博客，但是很多博客要么过于简略，要么是互相转载的，有一些博客图和代码还有点问题，也导致自己这个萌新走了不少弯路。所以自己重新整理了看的博客，力求以更简单的方式展现这个问题的解答办法，方便日后自己回顾。如果朋友们觉得写的有问题的地方，非常欢迎大家在下面留言交流，避免因为我的问题导致读者走弯路。

二、交并比的概念及应用

假设平面坐标中有一个矩形，并且这个矩形的长和宽均分别与x轴和y轴平行。

那么矩形在平面坐标中的唯一位置可以通过对角线上的两个顶点坐标来确定（这里不做证明）。

如下图所示：这个矩形的唯一位置可以用左上和右下的顶点坐标，即：（xmin, ymax, xmax, ymin)来确定，也可以用左下和右上顶点坐标，即（xmin, ymin, xmax, ymax)来确定。

接下来说一下自己踩的坑：网上的大部分博客，图是标的是左上和右下的顶点坐标，但是代码清一色是通过左下和右上顶点坐标来确定矩形位置的。所以一开始看着特别晕圈。

理论上两种确定方式都可以，不过相对而言，通过左下和右上两个顶点坐标，即（xmin, ymin, xmax, ymax)来确定矩形位置更符合我们的习惯，我想这也是网上大部分代码都是这样的原因吧。

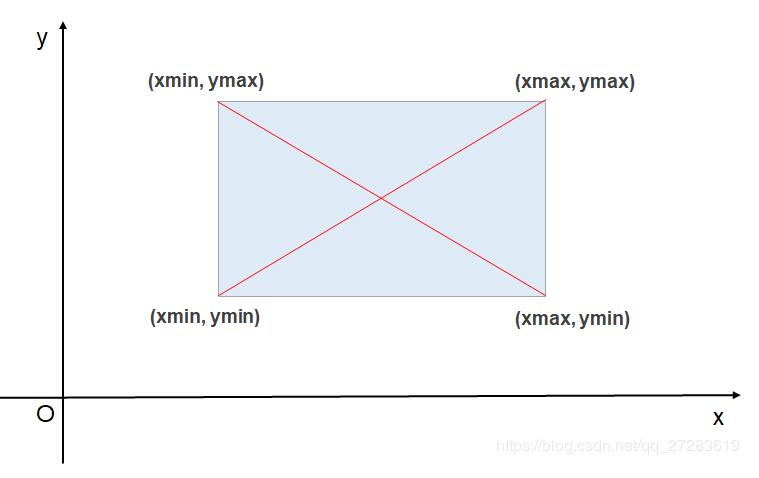
矩形的面积很好求，长X宽就行：

矩形的面积 = （xmax -xmin) X (ymax - ymin)

好了，理清楚怎么确定矩形的位置后，接下来我们就来解决交并比的计算问题。

交并比（Intersection over Union, IoU）是目标检测任务中的一个非常重要的概念。它是产生的预测框（Predicted bounding box）与原标记框（Ground-truth bounding box）的交叠率，即它们的交集（相交面积）与并集（总面积）的比值。最理想情况是完全重叠，即比值为1。一般来说，这个score ＞ 0.5 就可以被认为是一个不错的结果。这个标准用于测量真实和预测之间的相关度，相关度越高，该值越高，它可以评估算法的准确度。

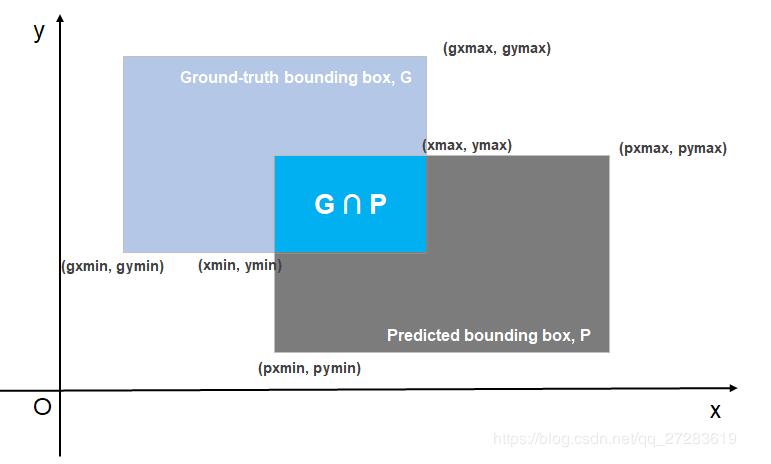
假设平面坐标中有两个矩形：原标记框（Ground-truth bounding box, G）和预测框（Predicted bounding box, P），其中G为手动标记的框，P为算法预测的框，并且这两个矩形的长和宽均分别与x轴和y轴平行。如下图所示：

IoU计算公式：

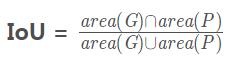
所以有：矩形G(gxmin, gymin, gxmax, gymax)和矩形P(pxmin, pymin, pxmax, pymax)

求交并比的关键是求出相交矩形G∩P的面积。

解决这个问题，我们只要确定相交矩形的左下（xmin, ymin）和右上（xmax, ymax）顶点坐标即可，即确定（xmin, ymin, xmax, ymax)。

通过看图，我们可以清楚的观察到：

# 相交矩形的左下顶点坐标, 就是两个矩形左下坐标的x和y分别取最大值
xmin = max(gxmin, pxmin)
ymin = max(gymin, pymin)
# 相交矩形的右上顶点坐标, 就是两个矩形右上坐标的x和y分别取最小值
xmax = min(gxmax, pxmax)
ymax = min(gymax, pyxmax)

如果一下没有看明白，可以自己在纸上多画画，理解下。

得到了相交矩形的坐标（xmin, ymin, xmax, ymax)那么相交矩形的面积就非常简单了。

area(G∩P) = 长 X 宽

w = xmax - xmin # 计算相交矩形的长

h = ymax - ymin # 计算相交矩形的宽

area(G∩P) = w X h # 计算相交矩形的面积

这里还有最后一个问题，当计算得到的宽或者长为0或者负数时，说明两个矩形不相交，相交面积为0，那么最后的IoU就为0。这里我们有两种处理方式：

1. 用if语句来分类讨论：

if w <=0 or h <= 0:
 return 0

2. 用max()方法来处理：

w = max(0, (x2 - x1))
h = max(0, (y1 - y2))

三、Python3 实现代码

经过以上分析，思路应该已经非常清晰了，这里我就直接放出完整Python3代码。

def calculate_IoU(predicted_bound, ground_truth_bound):
 """
 computing the IoU of two boxes.
 Args:
  box: (xmin, ymin, xmax, ymax),通过左下和右上两个顶点坐标来确定矩形位置
 Return:
  IoU: IoU of box1 and box2.
 """
 pxmin, pymin, pxmax, pymax = predicted_bound
 print("预测框P的坐标是：({}, {}, {}, {})".format(pxmin, pymin, pxmax, pymax))
 gxmin, gymin, gxmax, gymax = ground_truth_bound
 print("原标记框G的坐标是：({}, {}, {}, {})".format(gxmin, gymin, gxmax, gymax))

 parea = (pxmax - pxmin) * (pymax - pymin) # 计算P的面积
 garea = (gxmax - gxmin) * (gymax - gymin) # 计算G的面积
 print("预测框P的面积是：{}；原标记框G的面积是：{}".format(parea, garea))

 # 求相交矩形的左下和右上顶点坐标(xmin, ymin, xmax, ymax)
 xmin = max(pxmin, gxmin) # 得到左下顶点的横坐标
 ymin = max(pymin, gymin) # 得到左下顶点的纵坐标
 xmax = min(pxmax, gxmax) # 得到右上顶点的横坐标
 ymax = min(pymax, gymax) # 得到右上顶点的纵坐标

 # 计算相交矩形的面积
 w = xmax - xmin
 h = ymax - ymin
 if w <=0 or h <= 0:
  return 0

 area = w * h # G∩P的面积
 # area = max(0, xmax - xmin) * max(0, ymax - ymin) # 可以用一行代码算出来相交矩形的面积
 print("G∩P的面积是：{}".format(area))

 # 并集的面积 = 两个矩形面积 - 交集面积
 IoU = area / (parea + garea - area)

 return IoU

if __name__ == '__main__':
 IoU = calculate_IoU( (1, -1, 3, 1), (0, 0, 2, 2))
 print("IoU是：{}".format(IoU))

这里也放一下通过左上和右下顶点坐标来确定矩形的位置的Python3代码。原理是一样的，不要弄混就好。

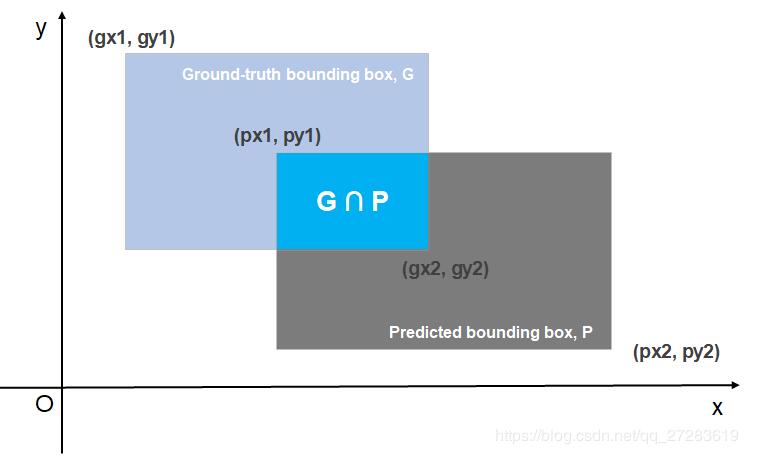
def calculate_IoU(predicted_bound, ground_truth_bound):
 """
 computing the IoU of two boxes.
 Args:
  box: (x1, y1, x2, y2),通过左上和右下两个顶点坐标来确定矩形
 Return:
  IoU: IoU of box1 and box2.
 """
 px1, py1, px2, py2 = predicted_bound
 print("预测框P的坐标是：({}, {}, {}, {})".format(px1, py1, px2, py2))

 gx1, gy1, gx2, gy2 = ground_truth_bound
 print("原标记框G的坐标是：({}, {}, {}, {})".format(gx1, gy1, gx2, gy2))

 parea = (px2 - px1) * (py1 - py2) # 计算P的面积
 garea = (gx2 - gx1) * (gy1 - gy2) # 计算G的面积
 print("预测框P的面积是：{}；原标记框G的面积是：{}".format(parea, garea))

 # 求相交矩形的左上和右下顶点坐标(x1, y1, x2, y2)
 x1 = max(px1, gx1) # 得到左上顶点的横坐标
 y1 = min(py1, gy1) # 得到左上顶点的纵坐标
 x2 = min(px2, gx2) # 得到右下顶点的横坐标
 y2 = max(py2, gy2) # 得到右下顶点的纵坐标

 # 利用max()方法处理两个矩形没有交集的情况,当没有交集时,w或者h取0,比较巧妙的处理方法
 # w = max(0, (x2 - x1)) # 相交矩形的长，这里用w来表示
 # h = max(0, (y1 - y2)) # 相交矩形的宽，这里用h来表示
 # print("相交矩形的长是：{}，宽是：{}".format(w, h))
 # 这里也可以考虑引入if判断
 w = x2 - x1
 h = y1 - y2
 if w <=0 or h <= 0:
  return 0

 area = w * h # G∩P的面积
 print("G∩P的面积是：{}".format(area))

 # 并集的面积 = 两个矩形面积 - 交集面积
 IoU = area / (parea + garea - area)

 return IoU

if __name__ == '__main__':
 IoU = calculate_IoU( (1, 1, 3, -1), (0, 2, 2, 0))
 print("IoU是：{}".format(IoU))

以上这篇浅谈Python3实现两个矩形的交并比(IoU)就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。