java实现哈夫曼压缩与解压缩的方法
一哈夫曼树以及文件压缩原理：
1.哈夫曼树 ：
给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近（频率越高的结点离根越进）。
以 下数组为例，构建哈夫曼树
int a[] = {0,1,2,3,4,5,6,7,8}
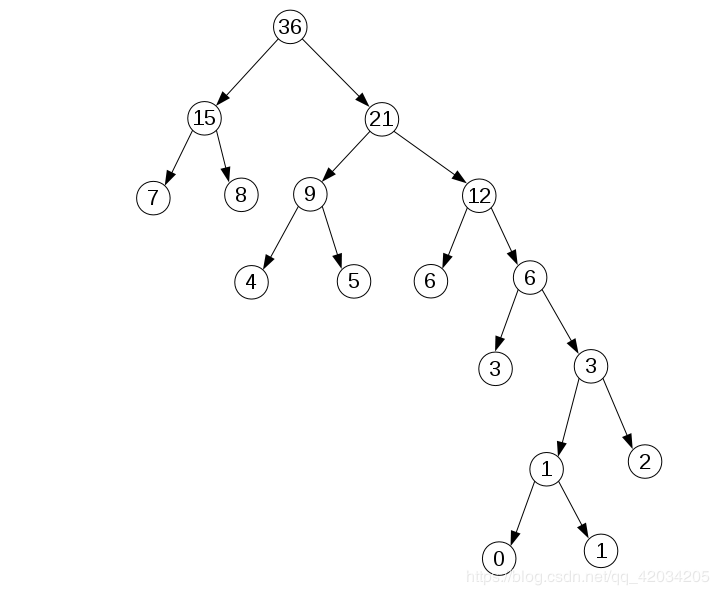
我们可以发现以下规律
1：9个数构成的哈夫曼树一共有17个结点，也就是可以n个数可以生产2*n-1个结点
2：数字越大的数离根节点越近，越小的数离根节点越近。
2.如何利用haffman编码实现文件压缩：
比如abc.txt文件中有以下字符：aaaabbbccde，
1.进行字符统计
aaaabbbccde a : 4次 b : 3次 c : 2次 d : 1次 e : 1次
2.用统计结果构建哈夫曼树
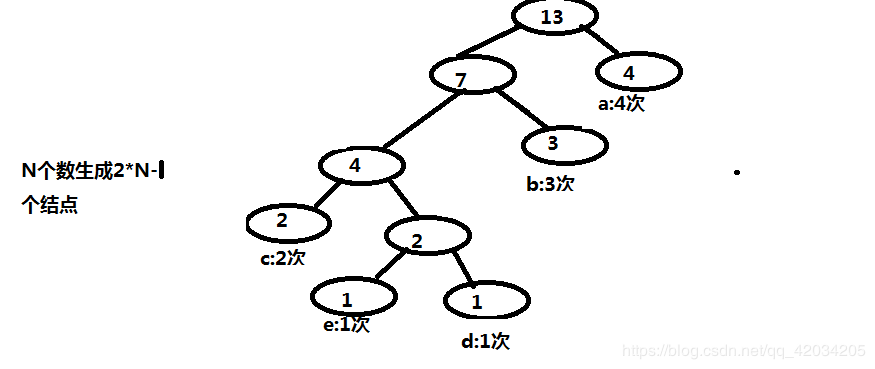
3.用哈夫曼树生成哈夫曼编码（从根结点开始，路径左边记为0，右边记为1）：
a的编码：1 b的编码:01 c的编码:000 d的编码:0011 e的编码:0010
4.哈夫曼编码代替字符，进行压缩。
源文件内容为：aaaabbbccde
将源文件用对应的哈夫曼编码（haffman code）替换，则有：11110101 01000000 00110010 （总共3个字节）
由此可见，源文件一共有11个字符，占11字节的内存，但是经过用haffman code替换之后，只占3个字节，这样就能达到压缩的目的
二主要技术点：
1.哈夫曼树算法（哈夫曼压缩的基本算法）
2.哈希算法（字符统计时候会用到，也可以直接用HashMap统计）
3.位运算（涉及到将指定位，置0或置1）
4.java文件操作，以及缓冲操作。
5.存储模式（大端存储，小端存储，能看懂文件16进制的形式）
7.设置压缩密码，解压输入密码解压（小编自己加的内容）
三实现过程：
以上述aaaabbbccde为例
1.字符统计：
public class FreqHuf {
public static int BUFFER_SIZE = 1 << 18;
int freq[] = new int[256];
File file;
int count;
List<HuffmanFreq> list;
FreqHuf(String pathname) throws Exception {
list = new ArrayList<>();
this.file = new File(pathname);
if(!file.exists()){
throw new Exception("文件不存在");
}
System.out.println("进行字符统计中");
CensusChar();
System.out.println("字符统计完毕");
}
public void CensusChar() throws IOException{
int intchar;
FileInputStream fis = new FileInputStream(file);
System.out.println("统计中");
//这种统计处理方案，速度极慢，不建议使用，以下采用缓存读数据。
// while((intchar = fis.read()) != -1){
// freq[intchar]++;
// }
//这里采用缓存机制，一次读1 << 18个字节，大大提高效率。
byte[] bytes = new byte[BUFFER_SIZE];
while((intchar = fis.read(bytes))!= -1){
for(int i = 0; i < intchar;i++){
int temp = bytes[i]& 0xff;
freq[temp]++;
}
}
fis.close();
for(int i = 0; i < 256; i++){
if(freq[i] != 0){
this.count++;
}
}
int index = 0;
for(int i = 0; i < 256; i++){
if(freq[i] != 0){
HuffmanFreq huffman = new HuffmanFreq();
huffman.character = (char)i;
huffman.freq = freq[i];
list.add(index, huffman);
}
}
}
}
//统计每个字符和其频率的类
public class HuffmanFreq {
char character;
int freq;
HuffmanFreq() {
}
HuffmanFreq(int character,int freq) {
this.character = (char)character;
this.freq = freq;
}
char getCharacter() {
return character;
}
void setCharacter(int character) {
this.character = (char)character;
}
int getFreq() {
return freq;
}
void setFreq(int freq) {
this.freq = freq;
}
byte[] infoToByte(){
byte[] bt = new byte[6];
byte[] b1 = ByteAnd8Types.charToByte(character);
for(int i= 0; i < b1.length;i++){
bt[i] = b1[i];
}
byte[] b2 = ByteAnd8Types.intToBytes2(freq);
int index = 2;
for(int i= 0; i < b2.length;i++){
bt[index++] = b2[i];
}
return bt;
}
@Override
public String toString() {
return "Huffman [character=" + character + ", freq=" + freq + "]";
}
}
2.用统计结果构建哈夫曼树：
//treeSize为总节点数
private void creatTree(int treeSize){
int temp;
treeList = new ArrayList<HuffTreeNode>();
for(int i = 0; i < treeSize; i++){
HuffTreeNode node = new HuffTreeNode();
treeList.add(i, node);
}
for(int i = 0; i < charCount; i++){
HuffTreeNode node = treeList.get(i);
node.freq.freq = charList.get(i).getFreq();
node.freq.character = charList.get(i).getCharacter();
node.left = -1;
node.right = -1;
node.use = 0;
}
for(int i = charCount; i < treeSize; i++){
int index = i;
HuffTreeNode node = treeList.get(i);
node.use = 0;
node.freq.character = '#';
node.right = searchmin(index);
node.left = searchmin(index);
node.freq.freq = treeList.get(node.right).freq.freq + treeList.get(node.left).freq.freq;
temp = searchmin(++index);
if(temp == -1){
break;
}
treeList.get(temp).use = 0;
}
}
private int searchmin(int count){
int minindex = -1;
for(int i = 0; i < count; i++){
if(treeList.get(i).use == 0){
minindex = i;
break;
}
}
if(minindex == -1){
return -1;
}
for(int i = 0; i < count; i++){
if((treeList.get(i).freq.freq <= treeList.get(minindex).freq.freq) && treeList.get(i).use == 0){
minindex = i;
}
}
treeList.get(minindex).use = 1;
return minindex;
}
3.用哈夫曼树生成哈夫曼编码（从根结点开始，路径左边记为0，右边记为1）：
private void bulidhuftreecode(int root, String str){
if(treeList.get(root).getLeft() != -1 && treeList.get(root).getRight() != -1){
bulidhuftreecode(treeList.get(root).getLeft(), str+"0");
bulidhuftreecode(treeList.get(root).getRight(), str + "1");
}
else{
treeList.get(root).code = str;
}
}
4.哈夫曼编码代替字符，进行压缩，压缩前首先要将文件头（文件标志，字符数量，最后一个字节有效位，密码）字符和其频率的那张表格写入文件，以便于解压缩
public void creatCodeFile(String path) throws Exception{
byte value = 0;
int index = 0;
int arr[] = new int[256];
int intchar;
for(int i = 0; i < charCount; i++){
arr[treeList.get(i).freq.character] = i;
}
File file = new File(path);
if(!file.exists()){
if(!file.createNewFile()){
throw new Exception("创建文件失败");
}
}
int count = charList.size();
HuffmanHead head = new HuffmanHead(count, howlongchar(count), password);
//将文件头信息写入文件
this.write = new RandomAccessFile(file, "rw");
write.write(head.InfoToByte());
//将字符及其频率的表写入文件
for(HuffmanFreq freq : charList){
byte[] bt = freq.infoToByte();
write.write(bt);
}
//将字符用哈夫曼编码进行压缩，这里读写都是采用缓存机制
byte[] readBuffer = new byte[BUFFER_SIZE];
while((intchar = read.read(readBuffer))!= -1){
ProgressBar.SetCurrent(read.getFilePointer());
for(int i = 0; i < intchar;i++){
int temp = readBuffer[i]& 0xff;
String code = treeList.get(arr[temp]).code;
char[] chars = code.toCharArray();
for(int j = 0; j < chars.length; j++){
if(chars[j] == '0'){
value = CLR_BYTE(value, index);
}
if(chars[j] == '1'){
value = SET_BYTE(value, index);
}
if(++index >= 8){
index = 0;
writeInBuffer(value);
}
}
}
}
//此方法速度较慢
// while((intchar = is.read()) != -1){
// String code = treeList.get(arr[intchar]).code;
// char[] chars = code.toCharArray();
//
// for(int i = 0; i < chars.length; i++){
// if(chars[i] == '0'){
// value = CLR_BYTE(value, index);
// }
// if(chars[i] == '1'){
// value = SET_BYTE(value, index);
// }
// if(++index >= 8){
// index = 0;
// oos.write(value);
// }
// }
// }
if(index != 0){
writeInBuffer(value);
}
byte[] Data = Arrays.copyOfRange(writeBuffer, 0, writeBufferSize);
write.write(Data);
write.close();
read.close();
}
//指定位，置1
byte SET_BYTE(byte value, int index){
return (value) |= (1 << ((index) ^ 7));
}
//指定位，置0
byte CLR_BYTE(byte value, int index){
return (value) &= (~(1 << ((index) ^ 7)));
}
//判断指定位是否为0,0为false,1为true
boolean GET_BYTE(byte value, int index){
return ((value) & (1 << ((index) ^ 7))) != 0;
}
如果一个字节一个字节往文件里写，速度会极慢，为了提高效率，写也采用缓存，先写到缓存区，缓存区满了后写入文件，
private void writeInBuffer(byte value) throws Exception {
if(writeBufferSize < BUFFER_SIZE){
writeBuffer[writeBufferSize] = value;
if(++writeBufferSize >= BUFFER_SIZE){
write.write(writeBuffer);
writeBufferSize = 0;
}
} else{
throw new Exception("写入文件出错");
}
}
到这里压缩就完成了，以下为解压缩方法
1.从写入文件中的字符统计的表读出放入list里
public void init() throws Exception{
char isHUf = read.readChar();
//验证文件头信息
if(isHUf != '哈'){
throw new Exception("该文件不是HUFFMAN压缩文件");
}
this.charCount = read.readChar();
this.treeSize = 2*charCount -1;
this.lastIndex = read.readChar();
int password = read.readInt();
if(password != this.password.hashCode()){
System.out.println("密码错误");
} else{
System.out.println("密码正确，正在解压");
}
//从文件中将字符统计的表读出
byte[] buffer = new byte[charCount * 6];
read.seek(10);
read.read(buffer, 0, charCount * 6);
ProgressBar.SetCurrent(read.getFilePointer());
for(int i = 0; i < buffer.length; i+=6){
byte[] buff = Arrays.copyOfRange(buffer, i, i+2);
ByteBuffer bb = ByteBuffer.allocate (buff.length);
bb.put (buff);
bb.flip ();
CharBuffer cb = cs.decode (bb);
byte[] buff1 = Arrays.copyOfRange(buffer, i+2, i+6);
int size = ByteAnd8Types.bytesToInt2(buff1, 0);
HuffmanFreq freq = new HuffmanFreq(cb.array()[0], size);
charList.add(freq);
}
}
2.用统计结果构建哈夫曼树（和以上代码一样）
3.用哈夫曼树生成哈夫曼编码（从根结点开始，路径左边记为0，右边记为1）（和以上代码一样）
4.遍历文件每个字节，根据哈夫曼编码找到对应的字符，将字符写入新文件
public void creatsourcefile(String pathname) throws Exception{
int root = treeList.size() - 1;
int fininsh = 1;
long len;
File file = new File(pathname);
if(!file.exists()){
if(!file.createNewFile()){
throw new Exception("创建文件失败");
}
}
write = new RandomAccessFile(file, "rw");
int intchar;
byte[] bytes = new byte[1<<18];
int index = 0;
while((intchar = read.read(bytes))!= -1){
len = read.getFilePointer();
ProgressBar.SetCurrent(len);
for(int i = 0; i < intchar;i++){
for(;index < 8 && fininsh != 0;){
if(GET_BYTE(bytes[i], index)){
root = treeList.get(root).right;
} else{
root = treeList.get(root).left;
}
if(treeList.get(root).right== -1 && treeList.get(root).left == -1){
byte temp = (byte)treeList.get(root).freq.character;
writeInBuffer(temp);
root = treeList.size() - 1;
}
index++;
if(len == this.goalfilelenth && i == intchar-1){
if(index >= this.lastIndex){
fininsh = 0;
}
}
}
index = 0;
}
}
byte[] Data = Arrays.copyOfRange(writeBuffer, 0, writeBufferSize);
write.write(Data);
write.close();
write.close();
read.close();
}
四运行展示：
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。
相关推荐
-
图文详解JAVA实现哈夫曼树
前言 我想学过数据结构的小伙伴一定都认识哈夫曼,这位大神发明了大名鼎鼎的"最优二叉树",为了纪念他呢,我们称之为"哈夫曼树".哈夫曼树可以用于哈夫曼编码,编码的话学问可就大了,比如用于压缩,用于密码学等.今天一起来看看哈夫曼树到底是什么东东. 概念 当然,套路之一,首先我们要了解一些基本概念. 1.路径长度:从树中的一个结点到另一个结点之间的分支构成这两个结点的路径,路径上的分支数目称为路径长度. 2.树的路径长度:从树根到每一个结点的路径长度之和,我们所说的完全
-
java实现哈夫曼压缩的实例
哈夫曼压缩的原理: 通过统计文件中每个字节出现的频率,将8位的01串转换为位数较短的哈夫曼编码. 其中哈夫曼编码是根据文件中字节出现的频率构建的,其中出现频率越高的字节,其路径长度越短; 出现频率越低的字节其路径长度越长.从而达到压缩的目的. 如何构造哈夫曼树? 一. 定义字节类 我的字节类定义了一下属性 public int data;//节点数据 public int weight;//该节点的权值 public int point;//该节点所在的左右位置 0-左 1-右 privat
-
Java 最优二叉树的哈夫曼算法的简单实现
最优二叉树也称哈夫曼树,讲的直白点就是每个结点都带权值,我们让大的值离根近.小的值离根远,实现整体权值(带权路径长度)最小化. 哈夫曼算法的思想我认为就是上面讲的,而它的算法实现思路是这样的: 从根结点中抽出权值最小的两个(涉及排序,但是我这个实现代码没做严格的排序,只有比较)合并出新的根结点重新加入排序(被抽出来的两个自然是变成非根结点了啊),就这样循环下去,直到合并完成,我们得到一颗最优二叉树--哈夫曼树. 说明: (1)哈夫曼树有n个叶子结点,则我们可以推出其有n-1个分支结点.因此我在定
-
java哈夫曼树实例代码
本文实例为大家分享了哈夫曼树java代码,供大家参考,具体内容如下 package boom; import java.util.ArrayDeque; import java.util.ArrayList; import java.util.Collections; import java.util.List; import java.util.Queue; class Node<T> implements Comparable<Node<T>>{ private T
-
java实现哈夫曼压缩与解压缩的方法
一哈夫曼树以及文件压缩原理: 1.哈夫曼树 : 给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树.哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近(频率越高的结点离根越进). 以 下数组为例,构建哈夫曼树 int a[] = {0,1,2,3,4,5,6,7,8} 我们可以发现以下规律 1:9个数构成的哈夫曼树一共有17个结点,也就是可以n个数可以生产2*n-1个结点 2:数字越大的数离根节点越近,越小的数离根节点越近.
-
Java之哈夫曼压缩原理案例讲解
1. 哈夫曼压缩原理 首先要明确一点,计算机里面所有的文件都是以二进制的方式存储的. 在计算机的存储单元中,一个ASCII码值占一个字节,1个字节等于8位(1Byte = 8bit) 可以参考这个网站: ASCII码在线转换计算器 以"JavaJavaJavaJavaJavaJava"这个字符串为例,它在计算机内部是这样存储的(每一个字符的ASCII码转换为二进制存储起来): public static void main(String[] args) { String beforeS
-
java实现哈夫曼文件解压缩
本文实例为大家分享了java实现哈夫曼文件解压缩的具体代码,供大家参考,具体内容如下 1.哈夫曼压缩对已经经过压缩处理的文件压缩率比较低,比如ppt和视频. 2.这个程序主要涉及到集合.树.IO相关知识. 字符的统计可以用map集合进行统计. 哈夫曼树的构建过程也并不复杂: ①先对树的集合按照根节点大小进行排序 ②拿出根节点数值最小的两棵树,用它两构建成一颗新的树: ③从集合中删除之前那两颗根节点最小的数: ④把新生成的树加入到集合中 一直循环重复上面的过程,直到集合的大小变成1为止: 写出.读
-
Java利用哈夫曼编码实现字符串压缩
赫夫曼编码基本介绍 1) 赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法 2) 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一. 3) 赫夫曼编码广泛地用于数据文件压缩.其压缩率通常在 20%-90%之间 4) 赫夫曼码是可变字长编码(VLC)的一种.Huffman 于 1952 年提出一种编码方法,称之为最佳编码 在通信领域中几种信息处理方式的区别(以字符串" i like like like java do you li
-
Java实现赫夫曼树(哈夫曼树)的创建
目录 一.赫夫曼树是什么? 1.路径和路径长度 2.节点的权和带权路径长度 3.树的带权路径长度 二.创建赫夫曼树 1.图文创建过程 2.代码实现 一.赫夫曼树是什么? 给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度(WPL)达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree).哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近. 图1 一棵赫夫曼树 1.路径和路径长度 在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径.
-
Android实现zip文件压缩及解压缩的方法
本文实例讲述了Android实现zip文件压缩及解压缩的方法.分享给大家供大家参考.具体如下: DirTraversal.java如下: package com.once; import java.io.File; import java.util.ArrayList; import java.util.LinkedList; /** * 文件夹遍历 * @author once * */ public class DirTraversal { //no recursion public sta
-
Python数据结构之哈夫曼树定义与使用方法示例
本文实例讲述了Python数据结构之哈夫曼树定义与使用方法.分享给大家供大家参考,具体如下: HaffMan.py #coding=utf-8 #考虑权值的haff曼树查找效率并非最高,但可以用于编码等使用场景下 class TreeNode: def __init__(self,data): self.data=data self.left=None self.right=None self.parent=None class HaffTree: def __init__(self): sel
-
如何用Java实现啥夫曼编码
大家可能会想,程序和第三方提供了很多压缩方式,何必自己写压缩代码呢?不错,如GZIP这样的压缩工具很多,可是在某些情况下(如文本内容小且字符不重复),GZIP压缩后会比原始文本还要大.所以在某些特殊情况下用自己的压缩方式可以更优. 大家可能早已忘记了在学校学习的哈夫曼知识,可以先在百度百科了解一下哈夫曼知识:http://baike.baidu.com/view/127820.htm 哈夫曼思想:统计文本字符重复率,求出各字符权值,再构造出一颗最优二叉树(又称哈夫曼树),然后给每个叶子结点生成一