Java数据结构之环形链表和约瑟夫问题详解

目录

• 一、环形链表
• 1、创建结点
• 2、添加小结点
• 3、显示循环链表
• 二、约瑟夫问题
• 1、问题描述
• 2、首先确定圈大小及开始位置
• 3、出圈操作
• 4、出圈方法完整代码
• 总结

一、环形链表

1、创建结点

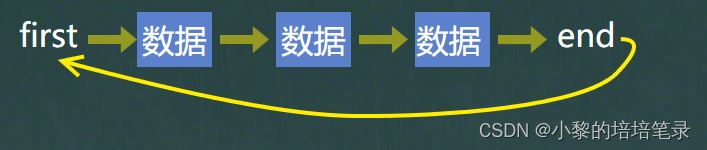
环形链表其实也很好理解，就是将单链表的头和尾连接起来，就形成了环形链表。

public class Node {
    public int data;
    public Node next;

    public Node(int data) {
        this.data = data;
    }

    @Override
    public String toString() {
        return "Node{" +
                "data=" + data +
                '}';
    }
}

2、添加小结点

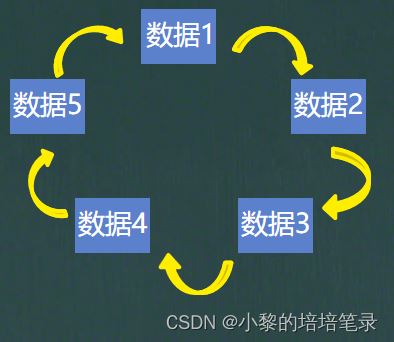
写一个方法用来添加结点，这个方法我们直接传入需要创建结点的个数，然后再方法中直接创建出一个简单的循环链表。代码解析：

//创建一个first结点，当前没有编号
public Node first = new Node(-1);

     public void add(int n){
        //其实循环链表，一个结点也可以循环，但这里为了方便后面介绍约瑟夫问题
        //我们循环的结点不能少于两个所以做了这个判断。
        if (n < 2){
            System.out.println("n的值不正确");
            return;
        }

        //辅助结点
        Node end = null;

        //使用for循环来创建链表
        for (int i = 1; i <= n; i++) {

            //根据编号创建结点
            Node node = new Node(i);

            //如果是第一个结点，first头指向第一个结点，end表示尾，回过头来指向first，形成循环
            if(i == 1){
                first = node;
                end = first;
            }else{
                //先将尾部end的next指向新的结点node，然后end后移指向新的结点，
                //再将end的next指向第一个结点first，这样就形成了循环
                end.next = node;
                end = end.next;
                end.next = first;
            }

        }
    }

3、显示循环链表

显示循环链表的方式和单链表的显示方式差不多，关键点在于如何判断循环链表的结束，我们的尾部是指向头部的，所以当尾部的next指向的结点等于头部，就是最后一个结点，此时就退出循环。

  public void show(Node first){

        //判断循环链表是否为空
        if (first.next == first){
            System.out.println("列表为空！");
            return;
        }

        //辅助结点
        Node temp = first;
        //循环打印
        while (true){

            System.out.println(temp);
            //最后一个结点的next等于first，就退出

            if (temp.next == first){
                break;
            }

            temp = temp.next;
        }
    }

二、约瑟夫问题

1、问题描述

约瑟夫(Joseph)问题的一种描述是:编号为1,2,...n的n个人按顺时针方向围坐一圈，每人持有一个密码(正整数)。开始选任一个正整数作为报数上限值m, 从第一个人开始按顺时针方向自1开始顺序报数, 报到m时停止报数。 报m的人出列, 将它的密码作为新的m值。 试设计一个程序求出出列顺序。

2、首先确定圈大小及开始位置

写一个方法

        start ：表示从哪一个位置开始

m ： 报多少个数，报到m个数的人出列

n ：圈总的大小

public void goOutCircle(int start,int m, int n){
}

确定圈的大小

        传入的n要多余两个人才能玩，然后传入的开始位置start不能在总人数之外，符合条件，我们调用前面我们介绍的方法add（）进行循环链表的创建。

        if (n >= 2 && start <= n){
            add(n);
        }else {
            System.out.println("输入异常！");
            return;
        }

确定开始位置

        first是指向链表的第一个的，但我们开始的位置可以是任何一个结点，所以先声明辅助结点temp，遍历循环链表，如果结点的data和传入的start的值相等，就找到了开始位置，将first 指向开始位置temp，然后循环就结束了。

        Node temp = first;
        while (true){
            if (temp.data == start){
                first = temp;
                break;
            }
            temp = temp.next;
        }

3、出圈操作

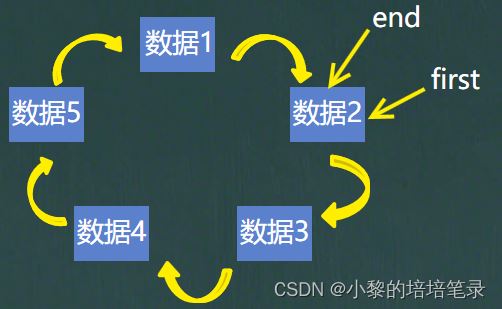
首先，我们需要一个辅助的结点end，然后假设开始位置在数据2的地方，first和end都指向数据2，数的次数为m = 2。

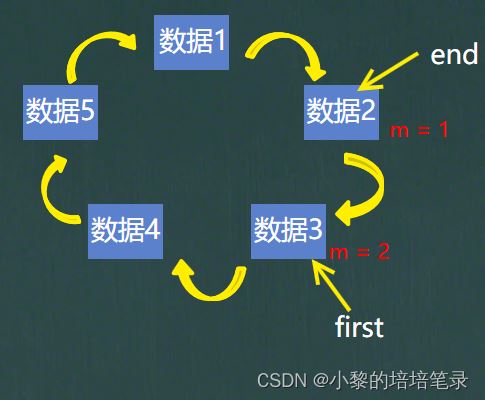
开始数数，数据3的位置是数数m = 2 的时候，这时数据3应该出圈。

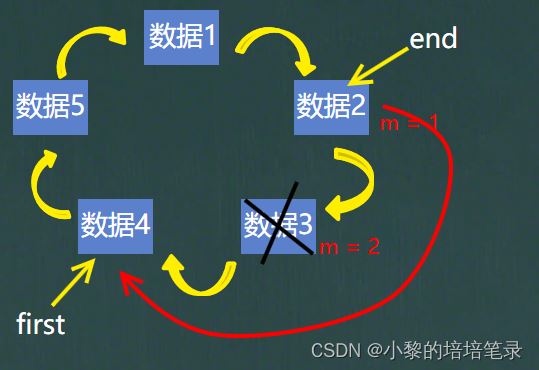
first继续指向要出圈数据的下一个结点，end所在的结点指向first指向的结点，就让数据3出圈了。

结点出圈后，first和end又同时指向一个结点，m 又开始重新计数 ，如此循环下去即可。

        Node end = first;

        while (true) {
            //当总数只有一个的时候，循环结束。
            if (n == 1) {
                System.out.println("胜利者为" + first + "号");
                break;
            }

            //用for循环，循环次数为 m - 1，因为本身要数一个数
            for (int i = 1; i <= m - 1; i++) {
                //first指向下一个结点
                first = first.next;
                //如果找到了要出圈的结点，first是正好指向它的
                if (i == m - 1) {
                    //first指向的这个结点出圈
                    System.out.println(first + "号出圈");
                    //每出圈一个，总数减一
                    n--;
                    //first继续指向下一个结点
                    first = first.next;
                    //此时end还在出圈结点的前一个位置，end的next指向first
                    end.next = first;
                    //end也同样指向first指向的结点
                    end = first;
                    break;
                }
                //如果没有到要出圈的结点，end继续跟着first指向同一个结点
                end = first;
            }
        }

4、出圈方法完整代码

    public void goOutCircle(int start,int m, int n){
        //首先确定圈的大小
        if (n >= 2 && start <= n){
            add(n);
        }else {
            System.out.println("输入异常！");
            return;
        }

        //确定数数的位置
        Node temp = first;
        while (true){
            if (temp.data == start){
                first = temp;
                break;
            }
            temp = temp.next;
        }

        //进行遍历
        Node end = first;
        while (true) {
            if (n == 1) {
                System.out.println("胜利者为" + first + "号");
                break;
            }

            for (int i = 1; i <= m - 1; i++) {
                first = first.next;
                if (i == m - 1) {
                    System.out.println(first + "号出圈");
                    n--;
                    first = first.next;
                    end.next = first;
                    end = first;
                    break;
                }
                end = first;
            }
        }
    }

运行结果：

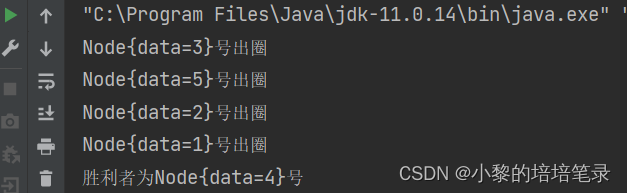
总结

到此这篇关于Java数据结构之环形链表和约瑟夫问题详解的文章就介绍到这了,更多相关Java环形链表和约瑟夫问题内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！