Java数据结构之红黑树的原理及实现

目录

• 为什么要有红黑树这种数据结构
• 红黑树的简介
• 红黑树的基本操作之旋转
• 红黑树之添加元素
• 红黑树之删除结点
• 删除结点没有儿子的情况
• 删除结点仅有一个儿子结点的情况
• 删除结点有两个儿子结点
• 红黑树动态可视化网站
• 红黑树参考代码

为什么要有红黑树这种数据结构

我们知道ALV树是一种严格按照定义来实现的平衡二叉查找树，所以它查找的效率非常稳定，为O(log n),由于其严格按照左右子树高度差不大于1的规则，插入和删除操作中需要大量且复杂的操作来保持ALV树的平衡（左旋和右旋），因此ALV树适用于大量查询，少量插入和删除的场景中

那么假设现在假设有这样一种场景：大量查询，大量插入和删除，现在使用ALV树就不太合适了，因为ALV树大量的插入和删除会非常耗时间，那么我们是否可以降低ALV树对平衡性的要求从而达到快速的插入和删除呢？

答案肯定是有的，红黑树这种数据结构就应运而生了（因为ALV树是高度平衡的，所以查找起来肯定比红黑树快，但是红黑树在插入和删除方面的性能就远远不是ALV树所能比的了）

红黑树的简介

红黑树是一种特殊的二叉查找树，每个结点都要储存位表示结点的颜色，或红或黑

红黑树的特性(红黑树必须满足的5个条件)：

1）每个结点或红或黑

2）根结点是黑色

3）空叶子结点是黑色

4）如果一个结点是红色，那么它的子节点是黑色

5）从任意一个结点出发到空的叶子结点经过的黑结点个数相同

示意图：(红黑树首先是一颗搜索树，所以左子树点小于根结点，右子树大于根节点，等于根结点的按照自己的需要放左边和右边都是可以的）（红黑树不仅是一颗搜索树还是一颗非严格的平衡树）

现在有个问题：红黑树是怎么通过上面5条性质保证任意结点到空的叶子结点的所有路径中，没有一条路径会大于其他路径的两倍的呢？（换句话说就是它是如何确保任何一个结点的左右子树的高度差不会超过二者中较低那个的一倍的呢？）

先结合红黑树的5个性质分析一下红黑树的一些操作，我们可能就明白了！

建议学习红黑树前了解AVL树

红黑树的基本操作之旋转

红黑树的基本操作是添加和删除，在对红黑树进行添加和删除之后，都会用到旋转方法，为什么呢？道理很简单，因为添加或者删除红黑树中的结点之后，红黑树就发生了变化，可能不满足上面的5条性质了，这个时候就需要通过旋转操作来保证它依旧是一棵红黑树，旋转分为左旋和右旋（旋转操作仅仅只是用来调节结点的位置的，就是为了满足红黑树的性质5）

左旋

左旋是将X的右子树绕X逆时针旋转，使得X的右子树成为X的父亲，同时修改相关结点的引用，旋转之后，要求二叉查找树的属性依然满足

右旋

右旋是将X的左子树绕X顺时针旋转，使得X的左子树成为X的父亲，同时注意修改相关结点的引用，旋转之后要求仍然满足搜索树的属性

红黑树之添加元素

添加操作宏观过程：首先将红黑树当作一颗查找树一样将结点插入，然后将结点着为红色，最后通过旋转和重新着色的方法使之重新成为红黑树

将新加入的结点涂成红色的原因：

1）不违背红黑树的性质5：从任意一个结点出发到空叶子结点，经过的黑色结点个数相同

2）按照红黑树的性质4我们知道红黑树中黑结点的个数至少是红结点个数的两倍，所以新增结点的父亲结点是黑结点的概率比较大，如果新增结点的父节点为黑色，那么此时不需要再去进行任何调整操作，因此效率很高，所以新结点应该涂成红色

少违背一条性质，意味着我们后续的旋转和重新着色操作会简单很多

现在我们来看看新增一个红色的结点会违背红黑树的5条性质中的哪些？

1）每个结点或红或黑

2）根结点是黑色

3）空叶子结点是黑色

4）如果一个结点是红色，那么它的子节点是黑色

5）从任意一个结点出发到空的叶子结点经过的黑结点个数相同

1.显然没有违背

2.根据查找树的特定，插入操作不好改变根结点，所以也没有违背

3.插入的肯定不是空叶子结点，所以也没有违背

4.有可能违背！！！

5.插入结点涂成红色就是为了不违背第5条性质

现在我们来分析一下新增的结点（红色）插入之后可能面临的几种情况，以及他们的处理措施

1.插入的结点为根结点

将新插入的红色结点变成黑色结点，满足根结点为黑色结点的要求！

2.父亲结点为黑色结点

这个时候不需要进行任何调整操作，此时的树仍然是一颗标准的红黑树

3.父亲结点为红色结点的情况下，叔叔结点为红色结点（不用考虑左右）

解决方案：将叔叔和父亲结点改为黑色，爷爷结点改为红色，然后又将爷爷结点当作插入结点看待，一直进行上面的操作，直到当前结点为根结点，然后将根结点变成黑色

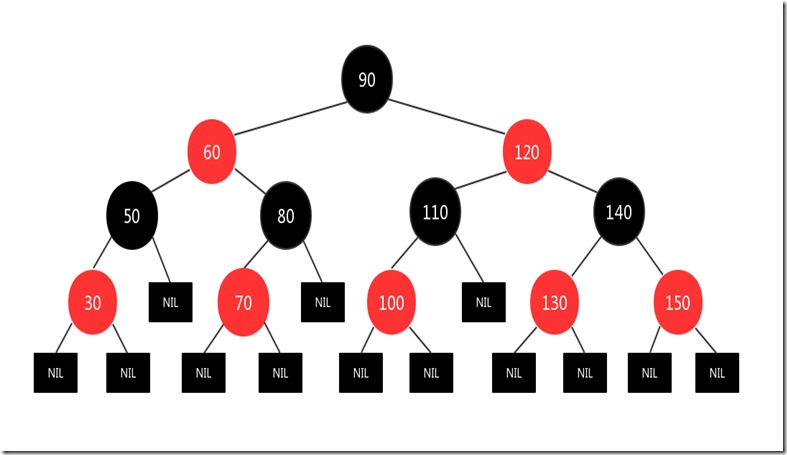
插入一个125的结点：

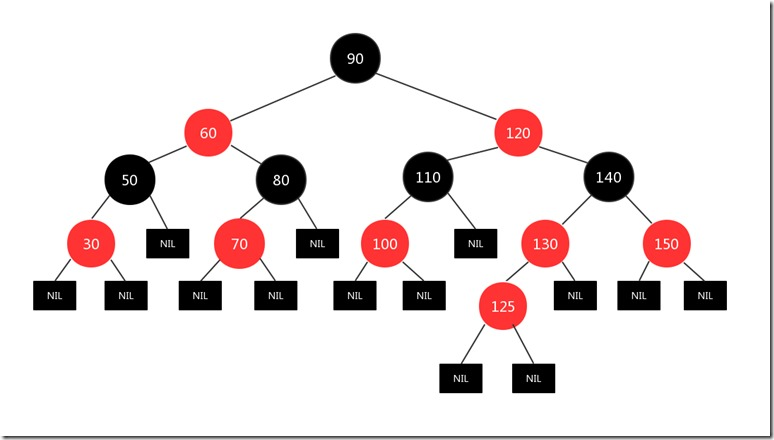
现在125结点和130结点都是红色的，显然违背了规则4，所以将新插入结点的父亲130结点和插入结点的叔叔结点150变成黑色，并将新插入结点的爷爷结点140变成红色，图如下：

然后又将140结点当作新插入结点处理（因为140结点和新插入结点面临的情况都是一样的：和父亲结点都是红色），也就是做如下处理：将140结点的父亲结点120和140的叔叔结点60变成黑色结点，将140结点的爷爷结点变成红色，因为遍历到了根结点，要满足根结点是黑色的性质要求，所以又将140的爷爷结点也就是根结点变成黑色，图如下：

到这里，为新插入结点125所做的某些结点重新着色的操作就完成了，现在该树是标准的红黑树了！

4.新插入的结点的父亲结点为红色，其叔叔结点为黑色

1）父亲结点为爷爷结点的左孩子，新插入结点为父节点的左孩子（左左情况）

2）父亲结点为爷爷结点的右孩子，新插入结点为父亲结点的右孩子（右右情况）

上述两种情况都是同一个处理办法

比如下图，新插入结点为25，其父亲结点30为红色，其叔叔结点为空黑色叶子结点，且新插入结点和其父节点都是左孩子：

我们将其父亲结点和爷爷结点颜色互换，然后针对爷爷结点进行一次左旋，图如下：

现在这颗树完全满足红黑树的5个性质了（最好自己对照5个性质看一下）

现在又一个问题，我们为什么要进行旋转？

假设我们只将新增结点的父亲结点和其爷爷结点的颜色互换了，图如下：

我们发现上述两条到叶子结点的路径经过的黑色结点数量不一样！！！，所以它不满足红黑树的第5条性质，所以这就是我们旋转的意义所在！！！（因为无论你这么旋转都没有改变结点颜色，改变的是结点的位置，而这位置改变刚好能使得树满足红黑树的第5条性质！）

5.新插入的结点的父亲结点是红色，其叔叔结点是黑色

1）插入结点是右结点，父节点是左结点

2）插入结点是左结点，父亲结点是右结点

上述两种情况都是同一个处理办法

比如下图，新插入结点是126，其父结点125为红色，其叔叔结点为空的黑色结点，而且插入结点是右结点，父结点是左结点

我们将父亲结点125看作当前结点进行左旋，旋转结果如下：

现在我们的当前结点是125，现在125的处境和上面的情况4是一样的（父节点为红，叔叔结点为黑，插入结点为左结点，父亲结点也为左孩子）现在我们继续按照情况4的处理办法处理上述情况（措施和情况4一样，父亲结点和爷爷结点互换颜色，然后针对爷爷结点进行左旋），处理后情况如下：

现在树就是一颗标准的红黑树了！

我们现在总结一下插入结点面临的几种情况以及采取的措施：

1.树为空，插入的结点为根结点

直接将插入的结点变成黑色

2.父亲结点为黑色结点

不需要任何操作

3.父亲结点为红色结点的情况下：

3.1 叔叔结点也为红色结点

将叔叔和父亲结点改为黑色，爷爷结点改为红色，未完，然后又将爷爷结点当作插入结点看待，一直进行上

面的操作，直到当前结点为根结点，然后将根结点变成黑色

3.2 叔叔结点为黑色结点的情况下：

3.2.1 （父亲结点为左孩子，插入结点也为左孩子）||（父亲结点为右孩子，插入结点也为右孩子）

将父亲结点和爷爷结点的颜色互换，然后针对爷爷结点进行一次左旋

3.2.2 （父亲结点为左孩子，插入结点为右孩子）||（父亲结点为右孩子，插入结点为左孩子）

针对父结点进行左旋，此时左旋后的情况必定是3.2.1的情况，然后按照3.2.1的情况处理

现在我们来推导一下，为什么插入的情况只有上面这些：

1.爷爷结点为红色结点的情况下，父亲结点只能为黑色（红黑树的性质4），处理操作：上面情况2

2.爷爷结点为黑色的情况下，父亲结点和叔叔结点：可以为红色，也可以为黑色

2.1 父亲结点为黑，叔叔结点为黑：处理操作：上面情况2

2.2 父亲结点为黑，叔叔结点为红：处理操作：上面情况2

2.3 父亲结点为红，叔叔结点为红：处理操作：上面情况3.1

（上面3种情况都是不用考虑左右的）

2.4 父亲结点为红，叔叔结点为黑：

• 2.4.1 父亲结点为左孩子，叔叔结点为左孩子：处理操作：上面情况3.2.1
• 2.4.2 父亲结点为右孩子，叔叔结点为右孩子：处理操作：上面情况3.2.1
• 2.4.3 父亲结点为左孩子，插入结点为右孩子：处理操作：上面情况3.2.2
• 2.4.4 父亲结点为右孩子，插入结点为左孩子：处理操作：上面情况3.2.2

总结：可以发现我们没有遗漏任何情况，所有可能面临的情况我们都处理了

红黑树之删除结点

先说一个删除结点的过程原理：首先将红黑树当作一个二叉查找树，将该结点从二叉查找树种删除，然后通过一些列重新着色操作等一系列措施来修正该树，使之重新成为一颗红黑树, 删除结点其实很容易，难的是如何使得删除结点后的树重新成为一个红黑树

我们可以根据删除结点N的儿子个数分为三种情况：

删除结点没有儿子

删除结点有1个儿子

删除结点有2个儿子

接下来我们又可以对以上三种情况继续进行细分:

一.删除结点没有儿子的情况：

• 1）删除结点为红色
• 2）删除结点为黑色，其兄弟结点没有儿子
• 3）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子为右孩子
• 4）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子为左孩子
• 5）删除结点为黑色，其兄弟结点有两个孩子，而且兄弟结点为红色
• 6）删除结点为黑色，其兄弟结点有两个孩子，而且兄弟结点为黑色

二. 删除结点只有一个儿子的情况：

• 1）删除结点为黑色，其唯一的儿子结点为红色（必定是红色，要不然不符合红黑树的第5条性质）
• 2）删除结点为红色，其儿子结点只能为黑：(红黑树中不存在这种情况，要不然无法满足红黑树第5条性质)

三. 删除结点有两个儿子的情况： 找到删除结点的右子树中最左的结点，两两值交换，然后删除结点的情况就变成了上面两种情况中的一种了

现在我们就具体分析一下面临不同的操作到达该这么操作：

删除结点没有儿子的情况

1）删除结点为红色

直接删除，比如下图，想要删除130结点

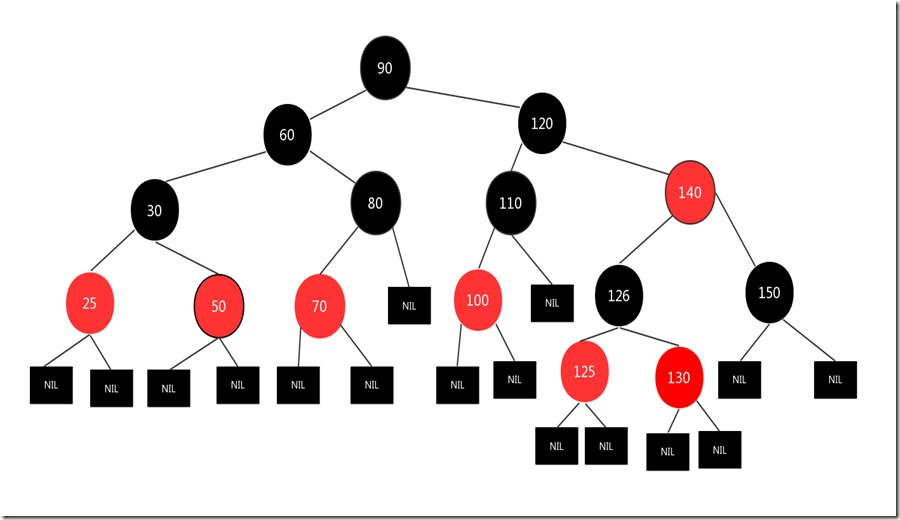
直接删除130结点，结果图如下：

因为删除的是红色结点，不会影响红黑树第5条性质，所以可以直接删除

2）删除结点为黑色，其兄弟结点没有儿子

这种情况下其兄弟结点也肯定是黑色的（要满足红黑树第5条性质），假设现在要删除的是150这个结点，原图如下：

先删除结点150，然后将兄弟结点126变成红色，父亲结点140变成黑色，结果如下：

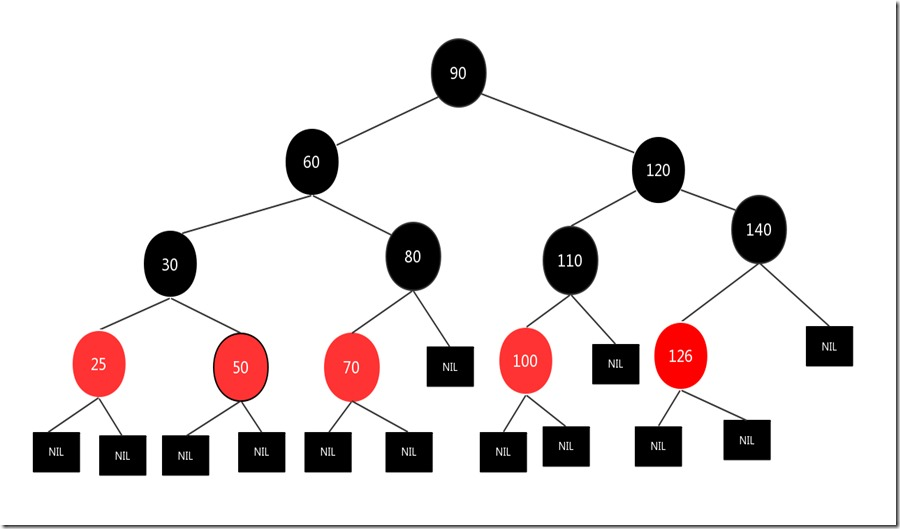
这样做的目的是为了满足红黑树的第5条性质，要不然根到最右边的叶子结点经过的黑色结点只有3个，而其他路径有4个

3）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子和兄弟结点在同一边（同为左子树或者同为右子树）

假设现在要删除的结点为110，其兄弟结点140只有一个孩子150，而且都是右子树，满足上述条件，原图如下：

先把需要删除的结点110删除，然后这个时候需要交换兄弟结点140和父亲结点120的颜色，并且把父亲结点120涂成黑色，把兄弟结点的子节点150涂成黑色

如果兄弟结点和兄弟结点的儿子都在右子树的话：对父亲结点进行左旋如果兄弟结点和兄弟结点的儿子都在左子树的话：对父亲结点进行右旋

上图是第一种情况，所以对父结点120进行左旋，结果如下：

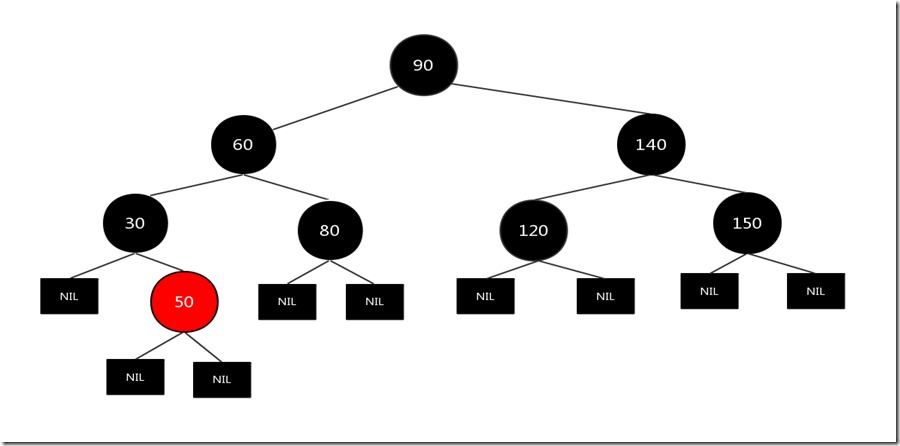
通过对某些结点重新着色和旋转，又将该树变成了一个标准的红黑树了

4）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子和兄弟结点不在同一边（右左或者左右的情况）

假设我们现在要删除的结点是80结点，其兄弟结点只有一个儿子，而且兄弟结点和兄弟结点的儿子是左右的情况（兄弟结点为左结点，兄弟结点的儿子为右结点），符合上述要求，原图如下：

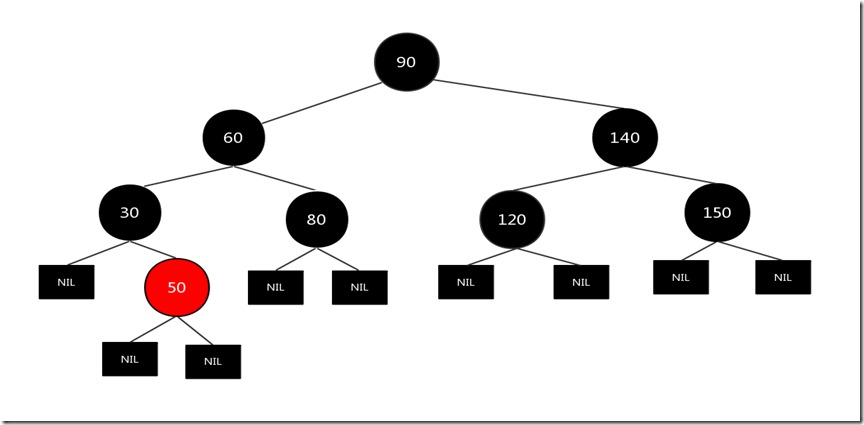
现在我们先将需要删除的80结点删除，然后将兄弟结点和兄弟结点的儿子结点颜色互换

如果兄弟结点是左子树，兄弟结点的儿子结点是右子树：对兄弟结点进行左旋

如果兄弟结点是右子树，兄弟结点的儿子结点是左子树：对兄弟结点进行右旋

上图的情况是进行左旋，也就是对兄弟结点30进行左旋，结果如下图：

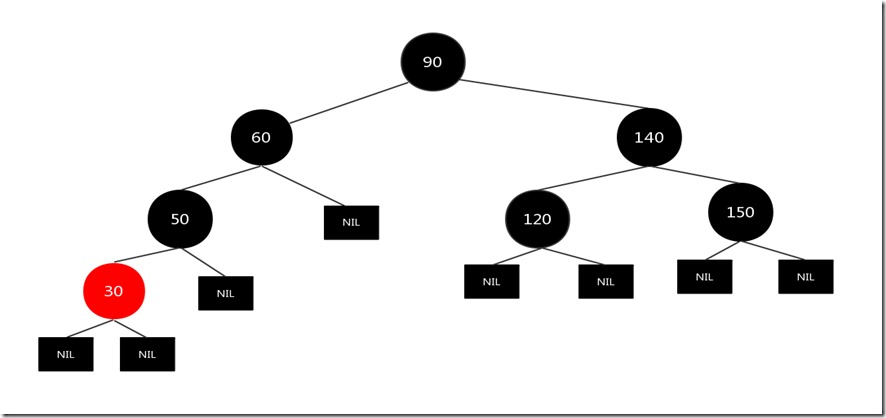
注意！！，现在还没有结束变换，我们发现变换之后的红黑树和情况3中的情况很相似，兄弟结点50和兄弟结点的子节点30处在同一边，我们可以按照情况3的处理办法进行处理：

交换兄弟结点50和父亲结点60的颜色，把父亲结点60和兄弟结点的子节点30涂成黑色

如果兄弟结点和兄弟结点的儿子都在右子树的话：对父亲结点进行左旋如果兄弟结点和兄弟结点的儿子都在左子树的话，对父亲结点进行右旋

上图的情况是第2中，所以对父亲结点60进行右旋，结果如下：

5)删除结点为黑色，其兄弟结点有两个孩子，兄弟结点为黑色而且两个孩子结点也为黑色

现在我们假设要删除的结点是130结点，其兄弟结点有两个孩子（可以把空的叶子结点看成黑色的儿子结点），而且兄弟结点和兄弟结点的儿子结点都是黑色，符合上述情况，原图如下：

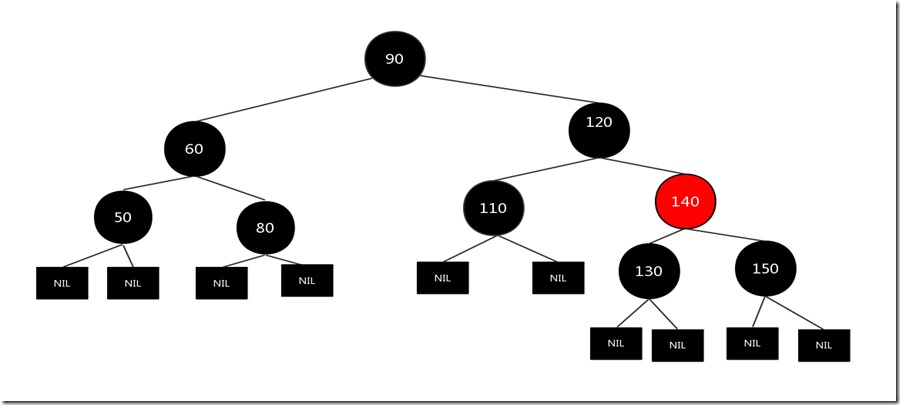
先直接删除需要删除的结点130，然后将父亲结点140和兄弟结点150颜色互换即可，结果如下：

6)删除结点为黑色，其兄弟结点有两个孩子，而且兄弟结点为红色

假设我们要删除的结点是110，其兄弟结点140为红色而且有两个孩子，原图如下：

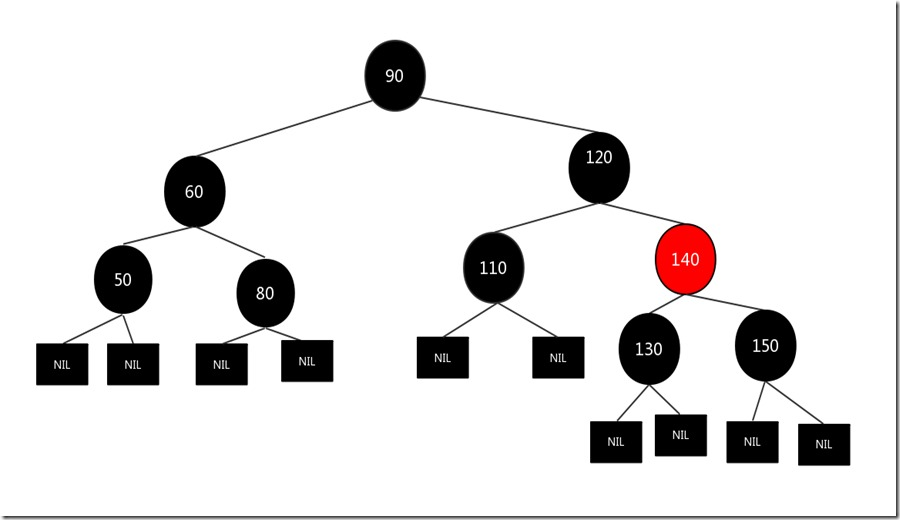
我们先交换兄弟结点140和父亲结点120的颜色

1.被删除的元素为左子树：对父亲结点左旋

2.被删除的元素为右子树：对父亲结点右旋

上图的情况是第一种情况，所以我们对父亲结点140进行左旋，按照上面操作之后（未完），结果如下：

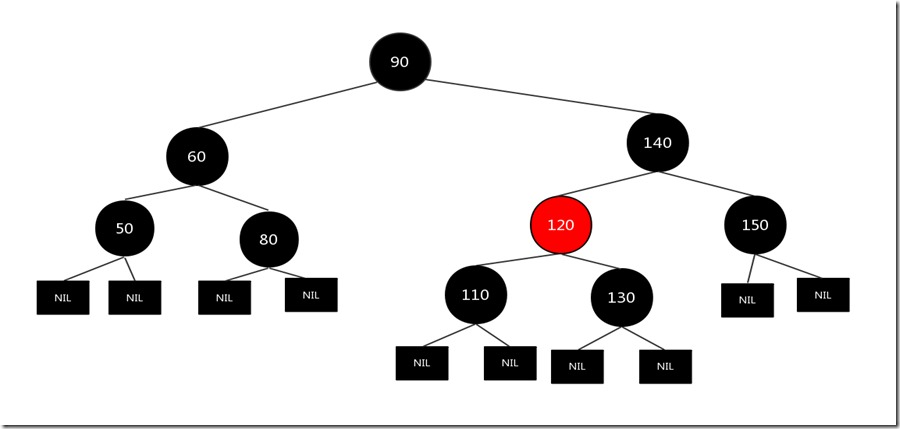
我们发现完成上述操作之后树还不是一个标准的红黑树（到叶子结点的一条路径黑色结点只有3个，而其他的路径有4个），我们发现现在红黑树的情况又和情况5的很像，所以我们按照情况5的做法继续：

我们要需要删除的结点还没有被删除（我特意留到最后删除的，就是为了在这里表示父亲结点是谁的父亲结点…）,现在我们将父亲结点120和兄弟结点130的颜色互换即可，结果如下：

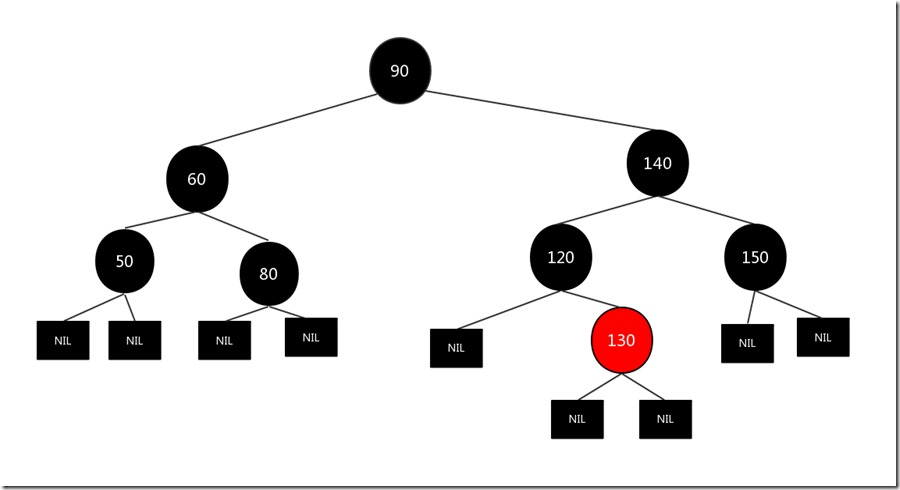
我们现在对删除结点没有儿子结点的6种删除情况进行一下总结：

删除结点没有儿子结点：

1）删除结点为红色：

直接删除

2）删除结点为黑色，其兄弟结点没有儿子：

兄弟结点变红，父亲结点变黑，然后将父亲结点当作当前结点按照这几种情形处理，直到当前结点为根结点

3）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子和兄弟结点在同一边（同为左子树或者同为右子树）：

1.不管是括号中那种情况，先交换兄弟结点和父亲结点的颜色，并且把父亲结点和兄弟结点的子结点涂成黑色

2.1如果兄弟结点和兄弟结点的儿子都在右子树的话：对父亲结点进行左旋

2.2如果兄弟结点和兄弟结点的儿子都在左子树的话：对父亲结点进行右旋

4）删除结点为黑色，其兄弟结点有一个孩子不空，并且该孩子和兄弟结点不在同一边（右左或者左右的情况）：

1.先将兄弟结点和兄弟结点的儿子结点颜色互换

2.1如果兄弟结点是左子树，兄弟结点的儿子结点是右子树：对兄弟结点进行左旋

2.2如果兄弟结点是右子树，兄弟结点的儿子结点是左子树：对兄弟结点进行右旋

3.将后续变换按照第3条处理

5)删除结点为黑色，其兄弟结点有两个孩子，兄弟结点为黑色而且两个孩子结点也为黑色：

1.将父亲结点和兄弟结点颜色互换

6）删除结点为黑色，其兄弟结点有两个孩子，而且兄弟结点为红色：

1.将兄弟结点和父亲结点的颜色互换

2.1 被删除的元素为左子树：对父亲结点左旋

2.2 被删除的元素为右子树：对父亲结点右旋

3.将后续变换按照第5条进行处理

以上6种情况讨论的都是删除结点没有儿子的情况（空叶子结点不算儿子结点）

现在我们来看看删除结点仅有一个儿子结点的情况！

删除结点仅有一个儿子结点的情况

1）删除结点为黑色，儿子结点无论左右都可以

比如我们要删除的结点是120结点，删除结点为黑色，唯一的儿子结点130为红色（必须是红色，不然违背红黑树第5条性质）原图如下：

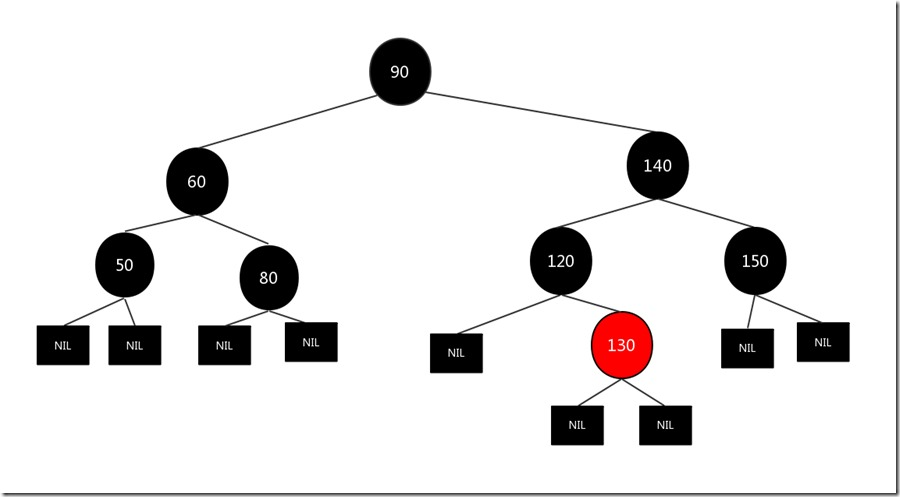
我们将需要删除的结点120删除，然后将子节点130涂黑放到被删除结点120的位置，结果如下：

2）删除结点为红色：其儿子结点只能为黑，红黑树中不存在这种情况，要不然无法满足红黑树第5条性质

总结一下删除结点只有一个儿子的情况：

1）删除结点为黑色，儿子结点无论左右都可以(将儿子结点涂成黑色放到被删除结点的位置)

下面我们来看看删除结点有两个儿子结点的情况

删除结点有两个儿子结点

找到删除结点的右子树中最左的结点，两两值交换，然后删除结点的情况就变成了上面两种情况中的一种了

删除结点只有一个儿子的情况

删除结点没有儿子的情况

比如下图

假设要删除的结点是120，先找到结点120右子树中最左的结点125，交换两者的值，图如下：

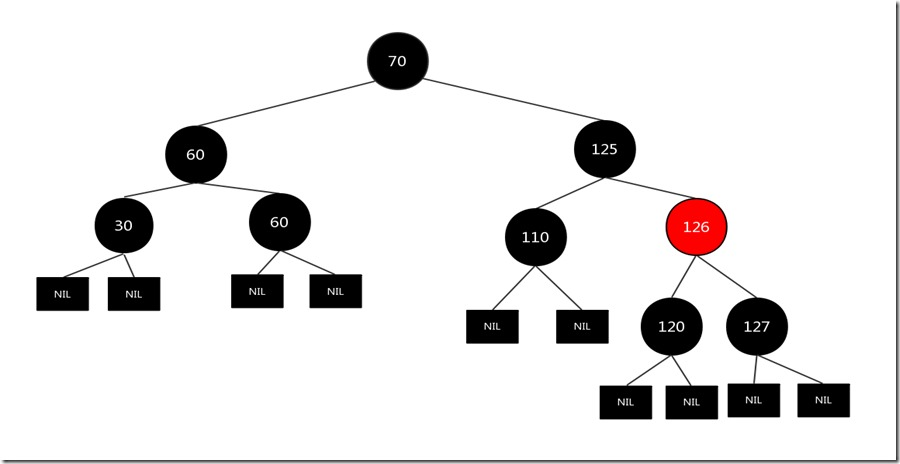
现在120仍然是要删除的结点，我们发现删除结点120没有一个儿子，而且其兄弟结点也没有儿子，那么其对应的情况为：

2）删除结点为黑色，其兄弟结点没有儿子：兄弟结点变红，父亲结点变黑

经过上面的变形，结果如下：

经过变换，该树变成了一颗标准的红黑树

所以当删除结点右两个儿子结点的时候，我们只需要按照搜索二叉树的删除方法替换删除值，这样就可以将情况变成删除结点没有儿子结点或者1个儿子结点的情况处理了

红黑树动态可视化网站

https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

红黑树参考代码

package com.tree.rbtree;

/**
 * Java 语言: 红黑树
 *
 * @author huanmin
 */

public class RBTree<T extends Comparable<T>> {

    private RBTNode<T> mRoot;    // 根结点

    private static final boolean RED   = false;
    private static final boolean BLACK = true;

    public class RBTNode<T extends Comparable<T>> {
        boolean color;        // 颜色
        T key;                // 关键字(键值)
        RBTNode<T> left;    // 左孩子
        RBTNode<T> right;    // 右孩子
        RBTNode<T> parent;    // 父结点

        public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) {
            this.key = key;
            this.color = color;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }

        public T getKey() {
            return key;
        }

        @Override
        public String toString() {
            return ""+key+(this.color==RED?"(R)":"B");
        }
    }

    public RBTree() {
        mRoot=null;
    }

    private RBTNode<T> parentOf(RBTNode<T> node) {
        return node!=null ? node.parent : null;
    }
    private boolean colorOf(RBTNode<T> node) {
        return node!=null ? node.color : BLACK;
    }
    private boolean isRed(RBTNode<T> node) {
        return ((node!=null)&&(node.color==RED)) ? true : false;
    }
    private boolean isBlack(RBTNode<T> node) {
        return !isRed(node);
    }
    private void setBlack(RBTNode<T> node) {
        if (node!=null) {
            node.color = BLACK;
        }
    }
    private void setRed(RBTNode<T> node) {
        if (node!=null) {
            node.color = RED;
        }
    }
    private void setParent(RBTNode<T> node, RBTNode<T> parent) {
        if (node!=null) {
            node.parent = parent;
        }
    }
    private void setColor(RBTNode<T> node, boolean color) {
        if (node!=null) {
            node.color = color;
        }
    }

    /*
     * 前序遍历"红黑树"
     */
    private void preOrder(RBTNode<T> tree) {
        if(tree != null) {
            System.out.print(tree.key+" ");
            preOrder(tree.left);
            preOrder(tree.right);
        }
    }

    public void preOrder() {
        preOrder(mRoot);
    }

    /*
     * 中序遍历"红黑树"
     */
    private void inOrder(RBTNode<T> tree) {
        if(tree != null) {
            inOrder(tree.left);
            System.out.print(tree.key+" ");
            inOrder(tree.right);
        }
    }

    public void inOrder() {
        inOrder(mRoot);
    }

    /*
     * 后序遍历"红黑树"
     */
    private void postOrder(RBTNode<T> tree) {
        if(tree != null)
        {
            postOrder(tree.left);
            postOrder(tree.right);
            System.out.print(tree.key+" ");
        }
    }

    public void postOrder() {
        postOrder(mRoot);
    }

    /*
     * (递归实现)查找"红黑树x"中键值为key的节点
     */
    private RBTNode<T> search(RBTNode<T> x, T key) {
        if (x==null) {
            return x;
        }

        int cmp = key.compareTo(x.key);
        if (cmp < 0) {
            return search(x.left, key);
        } else if (cmp > 0) {
            return search(x.right, key);
        } else {
            return x;
        }
    }

    public RBTNode<T> search(T key) {
        return search(mRoot, key);
    }

    /*
     * (非递归实现)查找"红黑树x"中键值为key的节点
     */
    private RBTNode<T> iterativeSearch(RBTNode<T> x, T key) {
        while (x!=null) {
            int cmp = key.compareTo(x.key);

            if (cmp < 0) {
                x = x.left;
            } else if (cmp > 0) {
                x = x.right;
            } else {
                return x;
            }
        }

        return x;
    }

    public RBTNode<T> iterativeSearch(T key) {
        return iterativeSearch(mRoot, key);
    }

    /*
     * 查找最小结点：返回tree为根结点的红黑树的最小结点。
     */
    private RBTNode<T> minimum(RBTNode<T> tree) {
        if (tree == null) {
            return null;
        }

        while(tree.left != null) {
            tree = tree.left;
        }
        return tree;
    }

    public T minimum() {
        RBTNode<T> p = minimum(mRoot);
        if (p != null) {
            return p.key;
        }

        return null;
    }

    /*
     * 查找最大结点：返回tree为根结点的红黑树的最大结点。
     */
    private RBTNode<T> maximum(RBTNode<T> tree) {
        if (tree == null) {
            return null;
        }

        while(tree.right != null) {
            tree = tree.right;
        }
        return tree;
    }

    public T maximum() {
        RBTNode<T> p = maximum(mRoot);
        if (p != null) {
            return p.key;
        }

        return null;
    }

    /*
     * 找结点(x)的后继结点。即，查找"红黑树中数据值大于该结点"的"最小结点"。
     */
    public RBTNode<T> successor(RBTNode<T> x) {
        // 如果x存在右孩子，则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
        if (x.right != null) {
            return minimum(x.right);
        }

        // 如果x没有右孩子。则x有以下两种可能：
        // (01) x是"一个左孩子"，则"x的后继结点"为 "它的父结点"。
        // (02) x是"一个右孩子"，则查找"x的最低的父结点，并且该父结点要具有左孩子"，找到的这个"最低的父结点"就是"x的后继结点"。
        RBTNode<T> y = x.parent;
        while ((y!=null) && (x==y.right)) {
            x = y;
            y = y.parent;
        }

        return y;
    }

    /*
     * 找结点(x)的前驱结点。即，查找"红黑树中数据值小于该结点"的"最大结点"。
     */
    public RBTNode<T> predecessor(RBTNode<T> x) {
        // 如果x存在左孩子，则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
        if (x.left != null) {
            return maximum(x.left);
        }

        // 如果x没有左孩子。则x有以下两种可能：
        // (01) x是"一个右孩子"，则"x的前驱结点"为 "它的父结点"。
        // (01) x是"一个左孩子"，则查找"x的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"。
        RBTNode<T> y = x.parent;
        while ((y!=null) && (x==y.left)) {
            x = y;
            y = y.parent;
        }

        return y;
    }

    /*
     * 对红黑树的节点(x)进行左旋转
     *
     * 左旋示意图(对节点x进行左旋)：
     *      px                              px
     *     /                               /
     *    x                               y
     *   /  \      --(左旋)-.           / \                #
     *  lx   y                          x  ry
     *     /   \                       /  \
     *    ly   ry                     lx  ly
     *
     *
     */
    private void leftRotate(RBTNode<T> x) {
        // 设置x的右孩子为y
        RBTNode<T> y = x.right;

        // 将 “y的左孩子” 设为 “x的右孩子”；
        // 如果y的左孩子非空，将 “x” 设为 “y的左孩子的父亲”
        x.right = y.left;
        if (y.left != null) {
            y.left.parent = x;
        }

        // 将 “x的父亲” 设为 “y的父亲”
        y.parent = x.parent;

        if (x.parent == null) {
            this.mRoot = y;            // 如果 “x的父亲” 是空节点，则将y设为根节点
        } else {
            if (x.parent.left == x) {
                x.parent.left = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
            } else {
                x.parent.right = y;    // 如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
            }
        }

        // 将 “x” 设为 “y的左孩子”
        y.left = x;
        // 将 “x的父节点” 设为 “y”
        x.parent = y;
    }

    /*
     * 对红黑树的节点(y)进行右旋转
     *
     * 右旋示意图(对节点y进行左旋)：
     *            py                               py
     *           /                                /
     *          y                                x
     *         /  \      --(右旋)-.            /  \                     #
     *        x   ry                           lx   y
     *       / \                                   / \                   #
     *      lx  rx                                rx  ry
     *
     */
    private void rightRotate(RBTNode<T> y) {
        // 设置x是当前节点的左孩子。
        RBTNode<T> x = y.left;

        // 将 “x的右孩子” 设为 “y的左孩子”；
        // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
        y.left = x.right;
        if (x.right != null) {
            x.right.parent = y;
        }

        // 将 “y的父亲” 设为 “x的父亲”
        x.parent = y.parent;

        if (y.parent == null) {
            this.mRoot = x;            // 如果 “y的父亲” 是空节点，则将x设为根节点
        } else {
            if (y == y.parent.right) {
                y.parent.right = x;    // 如果 y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
            } else {
                y.parent.left = x;    // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
            }
        }

        // 将 “y” 设为 “x的右孩子”
        x.right = y;

        // 将 “y的父节点” 设为 “x”
        y.parent = x;
    }

    /*
     * 红黑树插入修正函数
     *
     * 在向红黑树中插入节点之后(失去平衡)，再调用该函数；
     * 目的是将它重新塑造成一颗红黑树。
     *
     * 参数说明：
     *     node 插入的结点        // 对应《算法导论》中的z
     */
    private void insertFixUp(RBTNode<T> node) {
        RBTNode<T> parent, gparent;

        // 若“父节点存在，并且父节点的颜色是红色”
        while (((parent = parentOf(node))!=null) && isRed(parent)) {
            gparent = parentOf(parent);

            //若“父节点”是“祖父节点的左孩子”
            if (parent == gparent.left) {
                // Case 1条件：叔叔节点是红色
                RBTNode<T> uncle = gparent.right;
                if ((uncle!=null) && isRed(uncle)) {
                    setBlack(uncle);
                    setBlack(parent);
                    setRed(gparent);
                    node = gparent;
                    continue;
                }

                // Case 2条件：叔叔是黑色，且当前节点是右孩子
                if (parent.right == node) {
                    RBTNode<T> tmp;
                    leftRotate(parent);
                    tmp = parent;
                    parent = node;
                    node = tmp;
                }

                // Case 3条件：叔叔是黑色，且当前节点是左孩子。
                setBlack(parent);
                setRed(gparent);
                rightRotate(gparent);
            } else {    //若“z的父节点”是“z的祖父节点的右孩子”
                // Case 1条件：叔叔节点是红色
                RBTNode<T> uncle = gparent.left;
                if ((uncle!=null) && isRed(uncle)) {
                    setBlack(uncle);
                    setBlack(parent);
                    setRed(gparent);
                    node = gparent;
                    continue;
                }

                // Case 2条件：叔叔是黑色，且当前节点是左孩子
                if (parent.left == node) {
                    RBTNode<T> tmp;
                    rightRotate(parent);
                    tmp = parent;
                    parent = node;
                    node = tmp;
                }

                // Case 3条件：叔叔是黑色，且当前节点是右孩子。
                setBlack(parent);
                setRed(gparent);
                leftRotate(gparent);
            }
        }

        // 将根节点设为黑色
        setBlack(this.mRoot);
    }

    /*
     * 将结点插入到红黑树中
     *
     * 参数说明：
     *     node 插入的结点        // 对应《算法导论》中的node
     */
    private void insert(RBTNode<T> node) {
        int cmp;
        RBTNode<T> y = null;
        RBTNode<T> x = this.mRoot;

        // 1. 将红黑树当作一颗二叉查找树，将节点添加到二叉查找树中。
        while (x != null) {
            y = x;
            cmp = node.key.compareTo(x.key);
            if (cmp < 0) {
                x = x.left;
            } else {
                x = x.right;
            }
        }

        node.parent = y;
        if (y!=null) {
            cmp = node.key.compareTo(y.key);
            if (cmp < 0) {
                y.left = node;
            } else {
                y.right = node;
            }
        } else {
            this.mRoot = node;
        }

        // 2. 设置节点的颜色为红色
        node.color = RED;

        // 3. 将它重新修正为一颗二叉查找树
        insertFixUp(node);
    }

    /*
     * 新建结点(key)，并将其插入到红黑树中
     *
     * 参数说明：
     *     key 插入结点的键值
     */
    public void insert(T key) {
        RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null);

        // 如果新建结点失败，则返回。
        if (node != null) {
            insert(node);
        }
    }

    /*
     * 红黑树删除修正函数
     *
     * 在从红黑树中删除插入节点之后(红黑树失去平衡)，再调用该函数；
     * 目的是将它重新塑造成一颗红黑树。
     *
     * 参数说明：
     *     node 待修正的节点
     */
    private void removeFixUp(RBTNode<T> node, RBTNode<T> parent) {
        RBTNode<T> other;

        while ((node==null || isBlack(node)) && (node != this.mRoot)) {
            if (parent.left == node) {
                other = parent.right;
                if (isRed(other)) {
                    // Case 1: x的兄弟w是红色的
                    setBlack(other);
                    setRed(parent);
                    leftRotate(parent);
                    other = parent.right;
                }

                if ((other.left==null || isBlack(other.left)) &&
                        (other.right==null || isBlack(other.right))) {
                    // Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的
                    setRed(other);
                    node = parent;
                    parent = parentOf(node);
                } else {

                    if (other.right==null || isBlack(other.right)) {
                        // Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。
                        setBlack(other.left);
                        setRed(other);
                        rightRotate(other);
                        other = parent.right;
                    }
                    // Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。
                    setColor(other, colorOf(parent));
                    setBlack(parent);
                    setBlack(other.right);
                    leftRotate(parent);
                    node = this.mRoot;
                    break;
                }
            } else {

                other = parent.left;
                if (isRed(other)) {
                    // Case 1: x的兄弟w是红色的
                    setBlack(other);
                    setRed(parent);
                    rightRotate(parent);
                    other = parent.left;
                }

                if ((other.left==null || isBlack(other.left)) &&
                        (other.right==null || isBlack(other.right))) {
                    // Case 2: x的兄弟w是黑色，且w的俩个孩子也都是黑色的
                    setRed(other);
                    node = parent;
                    parent = parentOf(node);
                } else {

                    if (other.left==null || isBlack(other.left)) {
                        // Case 3: x的兄弟w是黑色的，并且w的左孩子是红色，右孩子为黑色。
                        setBlack(other.right);
                        setRed(other);
                        leftRotate(other);
                        other = parent.left;
                    }

                    // Case 4: x的兄弟w是黑色的；并且w的右孩子是红色的，左孩子任意颜色。
                    setColor(other, colorOf(parent));
                    setBlack(parent);
                    setBlack(other.left);
                    rightRotate(parent);
                    node = this.mRoot;
                    break;
                }
            }
        }

        if (node!=null) {
            setBlack(node);
        }
    }

    /*
     * 删除结点(node)，并返回被删除的结点
     *
     * 参数说明：
     *     node 删除的结点
     */
    private void
    remove(RBTNode<T> node) {
        RBTNode<T> child, parent;
        boolean color;

        // 被删除节点的"左右孩子都不为空"的情况。
        if ( (node.left!=null) && (node.right!=null) ) {
            // 被删节点的后继节点。(称为"取代节点")
            // 用它来取代"被删节点"的位置，然后再将"被删节点"去掉。
            RBTNode<T> replace = node;

            // 获取后继节点
            replace = replace.right;
            while (replace.left != null) {
                replace = replace.left;
            }

            // "node节点"不是根节点(只有根节点不存在父节点)
            if (parentOf(node)!=null) {
                if (parentOf(node).left == node) {
                    parentOf(node).left = replace;
                } else {
                    parentOf(node).right = replace;
                }
            } else {
                // "node节点"是根节点，更新根节点。
                this.mRoot = replace;
            }

            // child是"取代节点"的右孩子，也是需要"调整的节点"。
            // "取代节点"肯定不存在左孩子！因为它是一个后继节点。
            child = replace.right;
            parent = parentOf(replace);
            // 保存"取代节点"的颜色
            color = colorOf(replace);

            // "被删除节点"是"它的后继节点的父节点"
            if (parent == node) {
                parent = replace;
            } else {
                // child不为空
                if (child!=null) {
                    setParent(child, parent);
                }
                parent.left = child;

                replace.right = node.right;
                setParent(node.right, replace);
            }

            replace.parent = node.parent;
            replace.color = node.color;
            replace.left = node.left;
            node.left.parent = replace;

            if (color == BLACK) {
                removeFixUp(child, parent);
            }

            node = null;
            return ;
        }

        if (node.left !=null) {
            child = node.left;
        } else {
            child = node.right;
        }

        parent = node.parent;
        // 保存"取代节点"的颜色
        color = node.color;

        if (child!=null) {
            child.parent = parent;
        }

        // "node节点"不是根节点
        if (parent!=null) {
            if (parent.left == node) {
                parent.left = child;
            } else {
                parent.right = child;
            }
        } else {
            this.mRoot = child;
        }

        if (color == BLACK) {
            removeFixUp(child, parent);
        }
        node = null;
    }

    /*
     * 删除结点(z)，并返回被删除的结点
     *
     * 参数说明：
     *     tree 红黑树的根结点
     *     z 删除的结点
     */
    public void remove(T key) {
        RBTNode<T> node;

        if ((node = search(mRoot, key)) != null) {
            remove(node);
        }
    }

    /*
     * 销毁红黑树
     */
    private void destroy(RBTNode<T> tree) {
        if (tree==null) {
            return ;
        }

        if (tree.left != null) {
            destroy(tree.left);
        }
        if (tree.right != null) {
            destroy(tree.right);
        }

        tree=null;
    }

    public void clear() {
        destroy(mRoot);
        mRoot = null;
    }

    /*
     * 打印"红黑树"
     *
     * key        -- 节点的键值
     * direction  --  0，表示该节点是根节点;
     *               -1，表示该节点是它的父结点的左孩子;
     *                1，表示该节点是它的父结点的右孩子。
     */
    private void print(RBTNode<T> tree, T key, int direction) {

        if(tree != null) {

            if(direction==0)    // tree是根节点
            {
                System.out.printf("%2d(B) is root\n", tree.key);
            } else                // tree是分支节点
            {
                System.out.printf("%2d(%s) is %2d's %6s child\n", tree.key, isRed(tree)?"R":"B", key, direction==1?"right" : "left");
            }

            print(tree.left, tree.key, -1);
            print(tree.right,tree.key,  1);
        }
    }

    public void print() {
        if (mRoot != null) {
            print(mRoot, mRoot.key, 0);
        }
    }
}

以上就是Java数据结构之红黑树的原理及实现的详细内容，更多关于Java红黑树的资料请关注我们其它相关文章！