C语言数据结构中堆排序的分析总结

目录

• 一、本章重点
• 二、堆
• 2.1堆的介绍（三点）
• 2.2向上调整
• 2.3向下调整
• 2.4建堆（两种方式）
• 三、堆排序

一、本章重点

• 堆
• 向上调整
• 向下调整
• 堆排序

二、堆

2.1堆的介绍（三点）

1.物理结构是数组

2.逻辑结构是完全二叉树

3.大堆:所有的父亲节点都大于等于孩子节点，小堆：所有的父亲节点都小于等于孩子节点。

2.2向上调整

概念：有一个小/大堆，在数组最后插入一个元素，通过向上调整，使得该堆还是小/大堆。

使用条件：数组前n-1个元素构成一个堆。

以大堆为例：

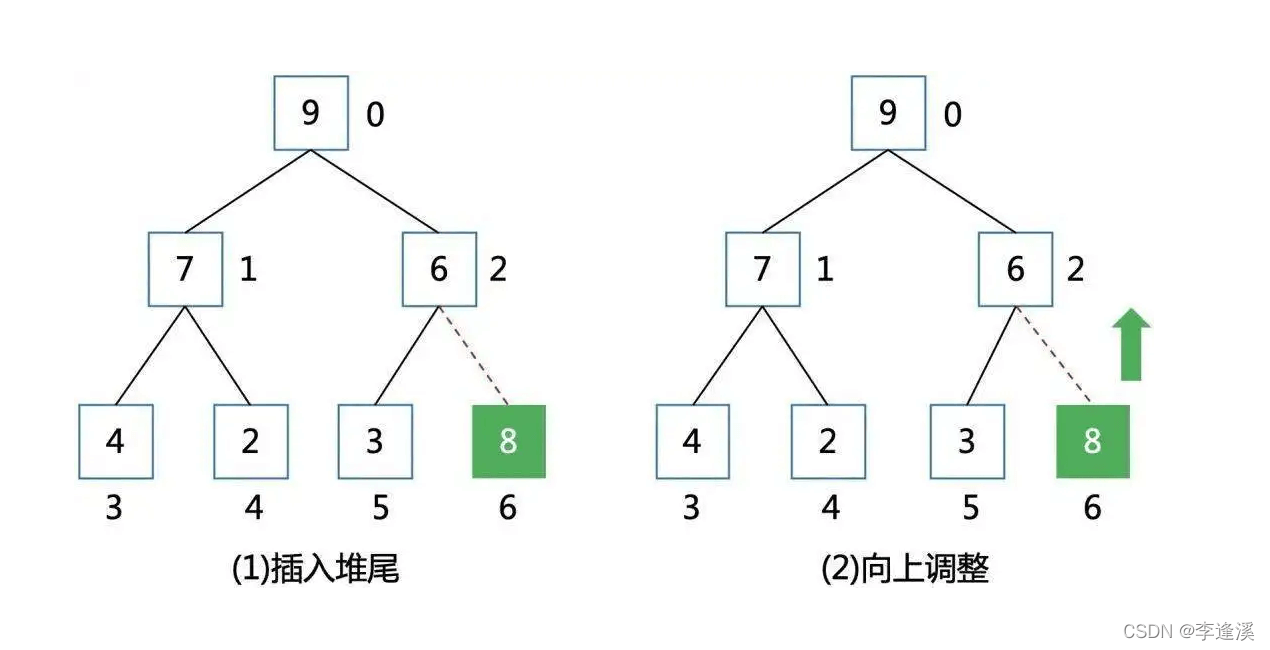
逻辑实现：

将新插入的最后一个元素看做孩子，让它与父亲相比，如果孩子大于父亲，则将它们交换，将父亲看做孩子，在依次比较，直到孩子等于0结束调整·。

如果中途孩子小于父亲，则跳出循环，结束调整。

参考代码：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])//如果孩子大于父亲，则将它们交换。
		{
			Swap(&a[child], &a[parent]);
            //迭代过程：
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
            //如果孩子小于父亲，结束调整
			break;
		}
	}
}

向上调整应用

给大\小堆加入新的元素之后仍使得大\小堆还是大\小堆。

2.3向下调整

概念：根节点的左右子树都是大\小堆，通过向下调整，使得整个完全二叉树都是大\小堆。

使用条件：根节点的左右子树都是大\小堆。

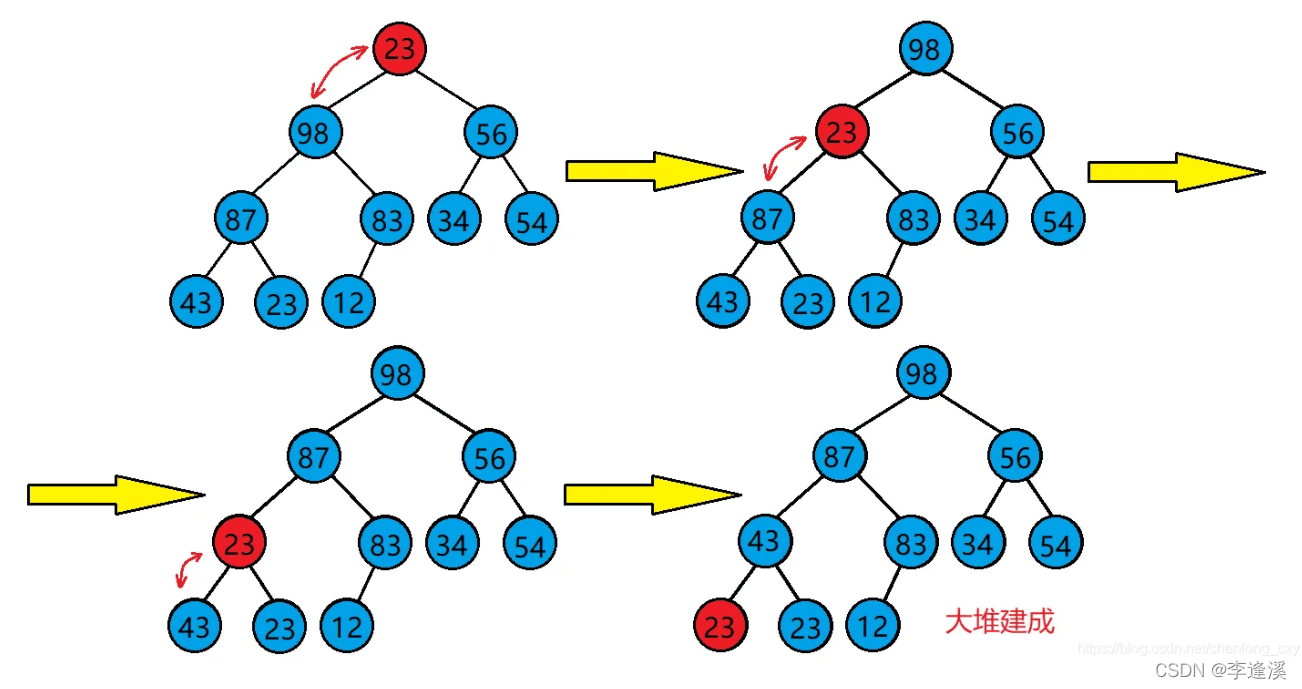
如图根为23，它的左右子树都是大堆，但整颗完全二叉树不是堆，通过向下调整可以使得整颗完全二叉树是堆。

逻辑实现：

选出根的左右孩子较大的那个孩子，然后与根比较，如果比根大，则交换，否则结束调整。

参考代码：

void AdjustDown(HPDataType* a, int size, int root)
{
	int parent = root;
	int child = parent * 2 + 1;//左孩子
	while (child < size)
	{
		if (child + 1 < size && a[child] < a[child + 1])//如果左孩子小于右孩子，则选右孩子
		{
			//务必加上child+1，因为当child=size-1时，右孩子下标是size，对其接引用会越界访问。
            child++;//右孩子的下标等于左孩子+1
		}
		if (a[child] > a[parent])//让较大的孩子与父亲比较，如果孩子大于父亲，则将它们交换。
		{
			Swap(&a[child], &a[parent]);
            //迭代过程
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

2.4建堆（两种方式）

第一种：向上调整建堆（时间复杂度是O（N*logN），空间复杂度O（1））

思路是：从第二个数组元素开始到最后一个数组元素依次进行向上调整。

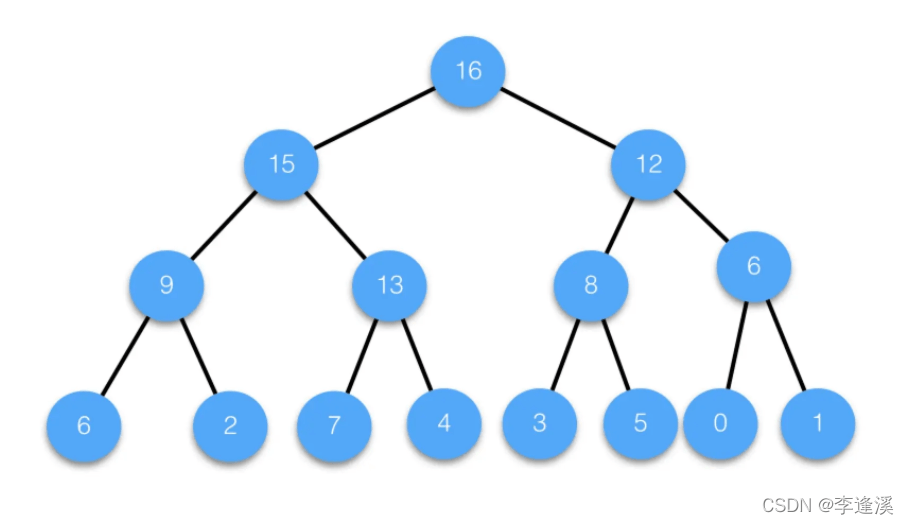
参考代码：

for (int i = 1; i < n; i++)
{
	AdjustUp(a, i);
}

时间复杂度计算：

以满二叉树进行计算

最坏情况执行步数为：T=(2^1)*1+(2^2)*2+(2^3)*3+....+2^(h-1)*(h-1)

最后化简得：T=2^h*(h-2)+2

又因为(2^h)-1=N

所以h=log(N+1)

带入后得T=(N+1)*(logN-1)+2

因此它的时间复杂度是：O（N*logN）

第二种：向下调整建堆（时间复杂度是O（N），空间复杂度是O（1））

从最后一个非叶子节点（最后一个数组元素的父亲）开始到第一个数组元素依次进行向下调整。

参考代码：

//n代表数组元素个数，j的初始值代表最后一个元素的父亲下标
for (int j = (n - 1 - 1) / 2; j >= 0; j--)
{
	AdjustDown(a, n, j);
}

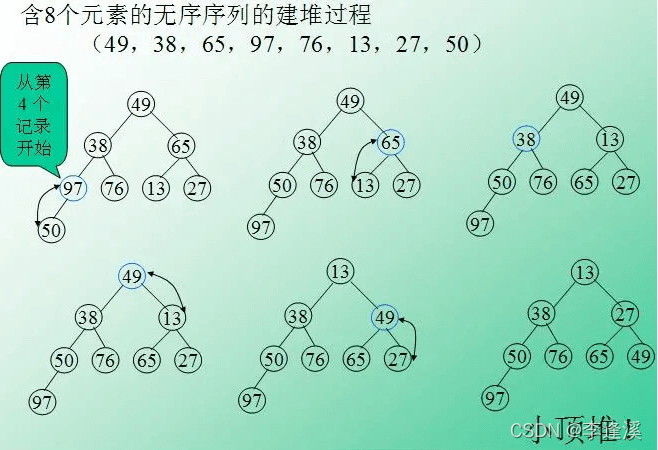
时间复杂度计算：

以满二叉树进行计算

最坏执行次数：

T=2^(h-2)*1+2^(h-3)*2+2^(h-4)*3+.....+2^3*(h-4)+2^2*(h-3)+2^1*(h-2)+2^0*(h-1)

联立2^h-1=N

化简得T=N-log（N+1）

当N很大时，log（N+1）可以忽略。

因此它的时间复杂度是O（N）。

因此我们一般建堆采用向下调整的建堆方式。

三、堆排序

目前最好的排序算法时间复杂度是O（N*logN）

堆排序的时间复杂度是O（N*logN）

堆排序是对堆进行排序，因此当我们对某个数组进行排序时，我们要先将这个数组建成堆，然后进行排序。

首先需要知道的是：

对数组升序，需要将数组建成大堆。

对数组降序，需要将数组建成小堆。

这是为什么呢？

这需要明白大堆和小堆的区别，大堆堆顶是最大数，小堆堆顶是最小数。

当我们首次建堆时，建大堆能够得到第一个最大数，然后可以将它与数组最后的元素进行交换，下一次我们只需要将堆顶的数再次进行向下调整，可以再次将数组变成大堆，然后与数组的倒数第二个元素进行交换，自此已经排好了两个元素，使得它们存储在需要的地方，然后依次进行取数，调整。

而如果是小堆，首次建堆时，我们能够得到最小的数，然后将它放在数组第一个位置，然后你要保持它还是小堆，该怎么办呢？只能从第二个元素开始从下建堆，而建堆的时间复杂度是O（N），你需要不断重建堆，最终堆排序的时间复杂度是O（N*N），这是不明智的。

或者建好小堆后，你这样做:

在开一个n个数组的空间，选出第一个最小数就将它放在新开辟的数组空间中保存，然后删除堆顶数，再通过向下调整堆顶的数，再将新堆顶数放在新数组的第二个位置.......。

虽然这样的时间复杂度是O（N*logN）。

但这样的空间复杂度是O（N）。

也不是最优的堆排序方法。

而建大堆的好处就在它把选出的数放在最后，这样我们就可以对堆顶进行向下调整，使得它还是大堆，而向下调整的时间复杂度是O(logN)，最终堆排序的时间复杂度是O（N*logN）。

堆排序的核心要义：

通过建大堆或者小堆的方式，选出堆中最大或者最小的数，从后往前放。

参考代码：

    int end = n - 1;//n代表数组元素的个数
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}

整个堆排序的代码：

void Swap(int* a, int* b)
{
	int temp = *a;
	*a = *b;
	*b = temp;
}

void AdjustUp(int* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void AdjustDown(int* a, int n, int root)
{
	int child = 2 * root + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child] < a[child+1])
		{
			child++;
		}
		if (a[child] > a[root])
		{
			Swap(&a[child], &a[root]);
			root = child;
			child = 2 * root + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	//建大堆(向上调整)
	//for (int i = 1; i < n; i++)
	//{
	//	AdjustUp(a, i);
	//}

	//建大堆(向下调整)
	for (int j = (n - 1 - 1) / 2; j >= 0; j--)
	{
		AdjustDown(a, n, j);
	}
	//升序
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}
void printarr(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}

int main()
{
	int arr[10] = { 9,2,4,8,6,3,5,1,10 };
	int size = sizeof(arr) / sizeof(arr[0]);
	HeapSort(arr, size);
	printarr(arr, size);
	return 0;
}

到此这篇关于C语言数据结构中堆排序的分析总结的文章就介绍到这了,更多相关C语言 堆排序内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！