C/C++实现图形学扫描线填充算法

在上图形学课的时候，学习了扫描线填充算法。不过在完成实验的时候在真正理解了该算法，在此记录一下，如果有表达上的错误，欢迎指正！

扫描线填充算法通过在与图形相交的第（1，2）、（3，4）... 边之间划线不断不断填充图形。因此，在扫描时就需要确定什么时候与图形的某条边相交、划线的时候x的范围是多少以及划线时是从哪个交点画至另一个交点。

结构体如下所示：

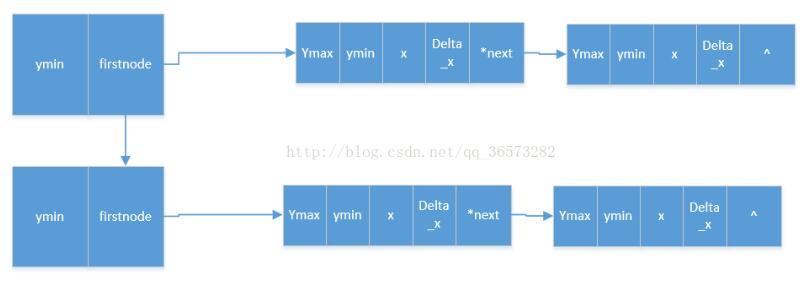
为了节省存储的空间，边表项也使用链表结构，将图形中ymin值相同的边链接在同一个边表项后，这样在扫描的时候方便添加。

具体的流程如下：

一、初始化活动边表

1. 统计并初始化表项

2. 将每条边分别链接在表项后

二、 绘制与填充

1. 取出当前与扫描线相交的边

① 取出ymin 大于当前扫描线的y值的边

② 删除ymax 小于等于当前扫描线的边（①②过程可以排除掉与扫描线平行的边）

2. 将取出的边按照左右顺序排序（根据边的最低点的坐标与直线的斜率判断）

3. 划线并直接在原结构上修改边的x值（因为是在一个函数内，修改保存的值仅限于函数内，并不影响main函数中的值）

具体的代码如下所示，使用的库是EasyX（可以在http://www.easyx.cn/下载）：

#include "graphics.h"
#include "stdio.h"
#include "conio.h"
#include <stdlib.h>
#include <math.h>
#include <cmath>
#include <iostream>

using namespace std;
#define MAX_VOL 20
//多边形的边的数据结构
typedef struct Edge
{
 int y_max, y_min; //该有向边的y坐标的最大值与最小值
 double x, deltax; //该有向边的x的最小值以及x的变化的量（1/斜率）
 struct Edge* next; //指向下一条边的指针

}Edge;
//活动边表表项
typedef struct TableItem
{
 int curr_y;  //该表项的y坐标值 ymin
 Edge *firstNode; //该表项的首个节点，如果没有，NULL
 struct TableItem *next; //指向下一个活动边表表项的指针
}TableItem;
//活动边表结构体
typedef struct Table
{
 TableItem *itemHeader; //活动边表的表项header
 int item_count; //活动边表表项的个数
}ET;

class Point
{
private:
 int x1, x2, y1, y2;
public:
 Point(int x1, int y1, int x2, int y2)
 {
 this->x1 = x1;
 this->x2 = x2;
 this->y1 = y1;
 this->y2 = y2;
 }
 //返回两个点之中的ymax
 int YMax()
 {
 return (y1 > y2 ? y1 : y2);
 }
 //返回ymin
 int YMin()
 {
 return (y1 < y2 ? y1 : y2);
 }
 //返回ymin 端点的x 值
 int x()
 {
 return (y1 < y2 ? x1 : x2);
 }
 //返回直线的斜率,按照传入的参数的顺序
 double KOfLine()
 {
 return ((y2 - y1)*1.0 / (x2 - x1));
 }

};

class Solution
{
public:
 //根据多边形初始化活动表
 //参数 T 活动边表
 //参数edges 用于初始化的边数组
 //参数 edge_num 用于初始化的边的个数
 void Init(ET &T, Edge *edges, int edge_num)
 {
 //初始化活动边表结构体
 T.item_count = 0;
 T.itemHeader = NULL;
 int ymins[20]; //存储ymin ,决定活动边表的个数以及表项的内容

 T.item_count = TableItemCount(edges, edge_num, ymins);
 T.itemHeader = (TableItem*)malloc(sizeof(TableItem));
 T.itemHeader->curr_y = ymins[0];
 T.itemHeader->firstNode = NULL;
 T.itemHeader->next = NULL;
 TableItem *p = T.itemHeader; //指向头结点
 for (int i = 1; i<T.item_count; ++i)
 {
  //依次创建活动边表的各个表项，并连接在一起
  TableItem *e = (TableItem*)malloc(sizeof(TableItem));
  e->curr_y = ymins[i];
  e->firstNode = NULL;
  e->next = NULL;
  p->next = e;
  p = e;
 }

 //按照用于初始化的边数组初始化活动边表
 p = T.itemHeader;
 for (int j = 0; j < edge_num; ++j) {
  this->AppendNode(T, edges[j].y_min, edges[j]);
 }
 //方法结束
 ////////测试区////////////
 //cout << "遍历表项。。。。。" << endl;
 //p = T.itemHeader;
 //while (p != NULL) {
 // cout << "当前表项y : " << p->curr_y << endl;
 // Edge *ele = p->firstNode;
 // while (ele != NULL) {
 // cout << "表项中的边： x = " << ele->x << " y_min = " << ele->y_min << " y_max = " << ele->y_max <<
 //  "deltax = " << ele->deltax << endl;
 // ele = ele->next;
 // }

 // p = p->next;
 //}
 ////////测试删除结点////////
 //p = T.itemHeader;
 //int yMax = 0;
 //while (yMax < 24) {
 // p = T.itemHeader;
 // cout << "-------------------------------" << endl;
 // cout << "当前y max :" << yMax << endl;
 // this->DeleteNode(T, yMax);
 // while (p != NULL) {
 // cout << "当前表项y : " << p->curr_y << endl;
 // Edge *ele = p->firstNode;
 // while (ele != NULL) {
 //  cout << "表项中的边： x = " << ele->x << " y_min = " << ele->y_min << " y_max = " << ele->y_max <<
 //  "deltax = " << ele->deltax << endl;
 //  ele = ele->next;
 // }
 // p = p->next;
 // }
 // yMax++;
 //}

 /////////////////////////

 }

 //用于根据边数组计算需要多少个表项
 //表项的个数取决于边的ymin的个数
 //返回值 ymin 数组
 //返回 item_num 表项的个数
 int TableItemCount(Edge *edges, int edge_num, int* ymins)
 {
 int count = 0;
 for (int i = 0; i<edge_num; ++i)
 {
  if (!isInArray(ymins, edges[i].y_min, count))
  {
  ymins[count++] = edges[i].y_min;
  }
 }
 //将ymin 升序排序
 for (int j = 0; j<count - 1; ++j)
 {
  for (int k = j + 1; k<count; ++k)
  {
  if (ymins[k] < ymins[j])
  {
   int tmp = ymins[k];
   ymins[k] = ymins[j];
   ymins[j] = tmp;
  }
  }
 }
 return count;

 }
 //判断一个整数是否在整数数组中
 bool isInArray(int *array, int e, int array_length)
 {
 for (int i = 0; i<array_length; ++i)
 {
  if (array[i] == e)
  {
  return true;
  }
 }
 return false;
 }

 //传入edges数组，初始化，返回Edge 结构体数组
 //因为需要是封闭图形，所以，在边数组中，最后的点的坐标设为起始点的坐标，传入的edge_num 不变
 Edge* InitEdges(int *edges, int edge_num)
 {
 Edge *newEdges = (Edge*)malloc(sizeof(Edge)*edge_num);
 int j = 0;
 for (int i = 0; i<edge_num; ++i)
 {
  Point point(edges[2 * i], edges[2 * i + 1], edges[2 * (i + 1)], edges[2 * (i + 1) + 1]);
  Edge *newEdge = (Edge*)malloc(sizeof(Edge));
  newEdge->x = (double)point.x();
  newEdge->y_max = point.YMax();
  newEdge->y_min = point.YMin();
  newEdge->deltax = 1.0 / point.KOfLine(); // 斜率分之一
  newEdge->next = NULL;
  newEdges[j++] = *(newEdge);
 }
 return newEdges;
 }
 //删除所有的小于ymax 的节点
 //参数 curr_ymax 当前扫描线的y值
 void DeleteNode(ET &T, int curr_ymax)
 {
 TableItem *p = T.itemHeader; //指向表项的指针
 while (p != NULL) {
  Edge *item = p->firstNode; //指向表项的邻接链表的指针
  Edge *itempre = p->firstNode;   //指向前一个边结点的指针
  while (item != NULL) {
  if (item->y_max <= curr_ymax) { //删除该结点
   T.item_count--; //当前活动边表中的边的个数-1
   //判断该结点是否是该链表的头结点
   if (item == p->firstNode) {
   p->firstNode = (Edge*)malloc(sizeof(Edge));
   p->firstNode = item->next;
   free(item);  //释放该结点
   item = p->firstNode; //重新指向firstnode结点
   itempre = p->firstNode;
   }
   else {
   itempre->next = item->next; //修改前一个结点的next的值
   free(item);   //删除该指针
   item = itempre->next; //继续向后遍历
   }
  }//if (item->y_max < curr_ymax)
  else {
   itempre = item;
   item = item->next;
  }
  }//while (item != NULL)
  p = p->next;
 }//while (p != NULL)

 }

 //将指定y值的节点添加到该表项, 该方法插入的顺序取决于调用该方法传入参数的顺序
 //该方法将新节点插入到对应表项的邻接链表的末尾
 void AppendNode(ET &T, int place_y, Edge &e)
 {
 ////////测试区//////////
 //cout << "In Append , place_y = " << place_y << " e.ymin = " << e.y_min << endl;
 //cout << "item count" << T.item_count << endl;

 ///////////////////////
 TableItem *p = T.itemHeader; //指向活动边表的头结点
 //将边e插入到对应的表项
 //之后在该表项中按照x的大小确定插入的位置
 for (int i = 0; i < T.item_count; ++i) {
  if (p->curr_y == e.y_min)
  break;
  p = p->next;
 }
 //将边插入到该表项的邻接链表中
 Edge *egp = p->firstNode; //egp 指向该表项的首个邻接节点
 if (egp == NULL) { //如果该表项还没有节点，直接插入
  egp = (Edge*)malloc(sizeof(Edge));
  *(egp) = e;
  egp->next = NULL;
  p->firstNode = egp;
 }
 else {
  Edge *pre = egp;
  while (egp != NULL) {
  pre = egp;
  egp = egp->next;
  }
  Edge *newedge = (Edge*)malloc(sizeof(Edge));
  *(newedge) = e;
  pre->next = newedge;
  newedge->next = NULL;
 }

 }

 //绘图的方法
 void Draw(ET T) {
 //首先取出ymin 值小于当前扫描线y 的边
 //按照顺序配对
 int curr_y = 0, curr_edge_num = 0, curr_gy = graphy(curr_y); //图形坐标的扫描线的y坐标
 Edge *currEdges = (Edge*)malloc(sizeof(Edge) * 20); //用于存放指针的数组
 //将每条边的记录的x 化为图形上的坐标
 TableItem *p = T.itemHeader;
 while (p != NULL) {
  Edge *q = p->firstNode;
  while (q != NULL) {
  q->x = graphx(q->x);
  q = q->next;
  }
  p = p->next;
 }

 for (; curr_y < 30; curr_gy--, curr_y = realy(curr_gy)) {
  this->DeleteNode(T, curr_y); //删除当前扫描过的边（ymax 小于 curr_y）
  currEdges = this->GetCurrEdges(T, curr_y, curr_edge_num); //获取当前与扫描线相交的边
  //对获取到的边进行排序、配对
  for (int i = 0; i < curr_edge_num - 1; ++i) {
  for (int j = i + 1; j < curr_edge_num; ++j) {
   if (this->IsRightTo(currEdges[i], currEdges[j])) {
   Edge tmp = currEdges[i];
   currEdges[i] = currEdges[j];
   currEdges[j] = tmp;
   }
  }

  }

  ////
 // getchar();
 // cout << "------------------------------" << endl;

  setcolor(BLUE);
  for (int j = 0; j < curr_edge_num / 2; ++j) {

  ///

  // cout << "line :" << (int)currEdges[2 * j].x << " , " << curr_y << "----->" << (int)currEdges[2 * j + 1].x << " , " << curr_y <<
  // " edge_num = " << curr_edge_num << endl;

  line((int)currEdges[2 * j].x, curr_gy, (int)currEdges[2 * j + 1].x, curr_gy);
  Edge *curr_edge1 = this->GetThisEdge(T, currEdges[2 * j].x, currEdges[2 * j].y_min,
   currEdges[2 * j].y_max); //获取当前边的指针，修改x值，保存修改
  curr_edge1->x += curr_edge1->deltax;
  Edge *curr_edge2 = this->GetThisEdge(T, currEdges[2 * j + 1].x, currEdges[2 * j + 1].y_min,
   currEdges[2 * j + 1].y_max);
  curr_edge2->x += curr_edge2->deltax;

  //line((int)currEdges[2 * j].x, curr_gy, (int)currEdges[2 * j + 1].x, curr_gy); //在两条直线之间划线
  //currEdges[2 * j].x += currEdges[2 * j].deltax;
  //currEdges[2 * j + 1].x += currEdges[2 * j + 1].deltax; //更新x 的坐标值
  }

  //////////测试模拟输出划线///////////////
  /*cout << "------------------------------------------" << endl;
  cout << "curr_y = " << curr_y << endl;
  cout << "当前扫描的边的个数 = " << curr_edge_num << endl;
  for (int i = 0; i < curr_edge_num / 2; ++i) {
  cout << "draw line bwtwen :" << endl;
  cout << "直线1 x = " << currEdges[2 * i].x << " ymin = " << currEdges[2 * i].y_min <<
   " ymax = " << currEdges[2 * i].y_max << endl;
  cout << "直线2 x = " << currEdges[2 * i + 1].x << " ymin = " << currEdges[2 * i + 1].y_min <<
   " ymax = " << currEdges[2 * i + 1].y_max << endl;

  }*/

  ////////////////////////////////////
  //在1,2 3,4 ... 边之间划线
  //TODO 坐标转换以及划线

 }

 ///////测试区/////////////////
 //cout << "-------------------------------------" << endl;
 //cout << "当前取出的边。。。。。。。。。。" << endl;
 //cout << "curr_edge_num = " << curr_edge_num << endl;
 //for (int i = 0; i < curr_edge_num; ++i) {
 // cout << "x = " << currEdges[i].x << " y_min = " << currEdges[i].y_min << " y_max = " << currEdges[i].y_max << endl;
 //}

 ////////////////////////////////

 }

 //返回某个边的指针
 //可通过此指针修改原结构体中边的x的值
 Edge* GetThisEdge(ET T, double x, int y_min, int y_max) {
 TableItem *p = T.itemHeader;
 while (p != NULL) {
  Edge *q = p->firstNode;
  while (q != NULL) {
  if ((q->x == x) && (q->y_max == y_max) && (q->y_min == y_min)) {
   return q;
  }
  q = q->next;
  }
  p = p->next;
 }

 return NULL;
 }

 //用于坐标转换的函数
 double graphx(double x) {
 return x * 10 + 100;
 }

 double realx(double gx) {
 return (gx - 100)*1.0 / 10;
 }

 int graphy(int y) {
 return 400 - y * 10;
 }

 int realy(int gy) {
 return (400 - gy) / 10;
 }

 //绘制坐标系
 void DrawCoordinate(int edges[], int edge_num) {
 line(100, 100, 100, 400);
 line(100, 400, 400, 400);
 outtextxy(85, 95, "y↑");
 outtextxy(400, 393, "→x");

 for (int i = 0; i < 30; ++i) {
  if (i % 2 != 0)
  continue;
  //TODO 字符转换
  outtextxy(i * 10 + 100, 390, "|");
  char *text = (char*)malloc(sizeof(char) * 10);
  itoa(i,text,10);
  outtextxy(i * 10 + 100, 410, text);
  free(text);
 }

 for (int j = 0; j < 30; ++j) {
  if (j % 2 != 0)
  continue;
  outtextxy(100, 400 - j * 10, "_");
  char *str = (char*)malloc(sizeof(char)*10);
  itoa(j,str,10);
  outtextxy(100, 400 - j * 10,str);
  free(str);
 }

 //绘制原多边形
 for (int k = 0; k < edge_num; ++k) {
  setcolor(YELLOW);
  int x1 = 0, x2 = 0, y1 = 0, y2 = 0;
  x1 = edges[2 * k] * 10 + 100;
  y1 = 400 - edges[2 * k + 1] * 10;
  x2 = edges[2 * (k + 1)] * 10 + 100;
  y2 = 400 - edges[2 * (k + 1) + 1] * 10;
  line(x1, y1, x2, y2);
 }

 }

 //获取当前的涉及的扫描线的边
 //即取出当前ymin 小于curr_y的边
 //通过参数返回取出的边的个数
 Edge* GetCurrEdges(ET T, int curr_y, int &edge_num) {
 Edge *currEdges = (Edge*)malloc(sizeof(Edge) * 20); //分配最大容量
 int i = 0;
 TableItem *p = T.itemHeader;
 while (p != NULL) {
  Edge *q = p->firstNode;
  while (q != NULL) {
  if (q->y_min <= curr_y) { //等于号很重要，否则会在图形中出现空白区
   currEdges[i++] = *q; //将当前边的值取出（不改变原活动表）
  }
  q = q->next;
  }
  p = p->next;
 }
 edge_num = i; //保存取出的边的个数
 return currEdges;
 }

 //判断edge1 是否在edge2 的右边的方法
 bool IsRightTo(Edge edge1, Edge edge2) {
 if (edge1.x > edge2.x) //如果edge1最低点的x坐标小于edge2的最低点的x的坐标，则edge1在edge2的右边
  return true;
 else {
  if (edge1.x < edge2.x)
  return false;
  double x_max1 = (edge1.y_max - (edge1.y_min - 1.0 / edge1.deltax*edge1.x))*edge1.deltax;
  double x_max2 = (edge2.y_max - (edge2.y_min - 1.0 / edge2.deltax*edge2.x))*edge2.deltax;
  if (x_max1 > x_max2)
  return true;
 }
 return false;
 }

};

int main()
{
 //TODO 测试活动边表初始化
 Solution solution;
 int edges[] = { 4,18,14,14,26,22,26,10,14,2,4,6,4,18 };
 Edge* newEdges = solution.InitEdges(edges, 6);
 ET T;
 solution.Init(T, newEdges, 6); //初始化活动边表

 initgraph(800, 800, SHOWCONSOLE);
 solution.DrawCoordinate(edges, 6);
 solution.Draw(T);
 getchar();
 closegraph();
 return 0;
}

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。