C语言 数据结构之中序二叉树实例详解

C语言数据结构 中序二叉树

前言：

线索二叉树主要是为了解决查找结点的线性前驱与后继不方便的难题。它只增加了两个标志性域，就可以充分利用没有左或右孩子的结点的左右孩子的存储空间来存放该结点的线性前驱结点与线性后继结点。两个标志性域所占用的空间是极少的，所有充分利用了二叉链表中空闲存的储空间。

要实现线索二叉树，就必须定义二叉链表结点数据结构如下（定义请看代码）：

说明：

1.       leftTag=false时，表示left指向该结点的左孩子；

2.       leftTag=true时，表示left指向该结点的线性前驱结点；

3.       rightTag=false时，表示right指向该结点的右孩子；

4.       rightTag=true时，表示right指向该结点的线性后继结点；

以二叉链表结点数据结构所构成的二叉链表作为二叉树的存储结构，叫做线索二叉链表；指向结点的线性前驱或者线性后继结点的指针叫做线索；加上线索的二叉树称为线索二叉树；对二叉树以某种次序遍历将其变为线索二叉树的过程叫做线索化。

中序次序线索化二叉树算法：

  中序次序线索化是指用二叉链表结点数据结构建立二叉树的二叉链表，然后按照中序遍历的方法访问结点时建立线索；(具体看代码)

检索中序二叉树某结点的线性前驱结点的算法：

1.       如果该结点的leftTag=true,那么left就是它的线性前驱；

2.       如果该结点的leftTag=false，那么该结点左子树最右边的尾结点就是它的线性前驱点；

（具体请看代码）

检索中序二叉树某结点的线性后继结点和算法：

1.       如果该结点的right=true,那么right就是它的线性后继结点；

2.       如果该结点的right=false,那么该结点右子树最左边的尾结点就是它的线性后继结点

（具体请看代码）

图：后继线索

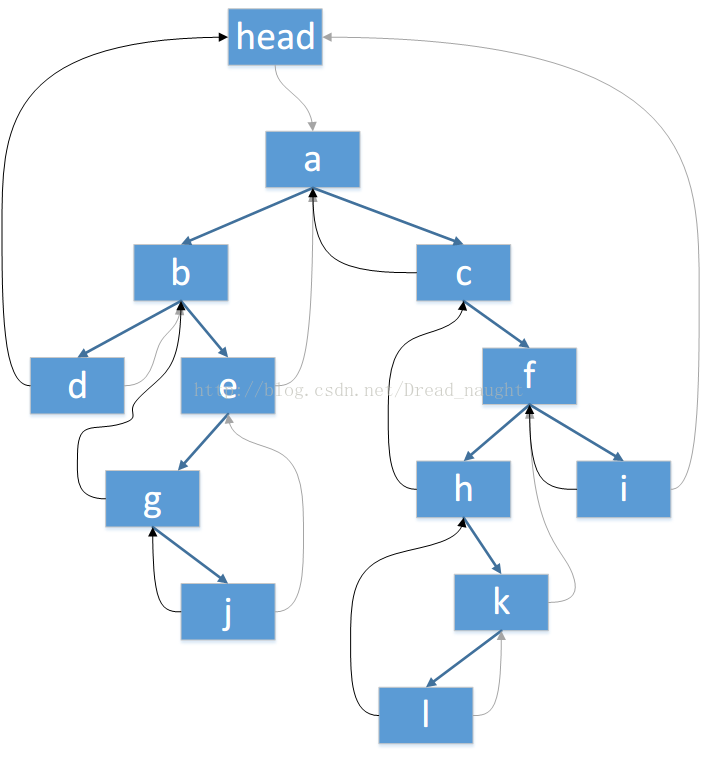
图：前驱线索

节点定义：

struct Node
{
  int data;
  bool leftTag;
  bool rightTag;
  Node* left;
  Node* right;
  Node(int _data):data(_data),left(0),right(0),leftTag(false),rightTag(false){}
}; 

类定义：

class BinaryTree
{
private:
  Node* root;
private:
  Node* head;
  Node* pre;
  void makeThread(Node* node);
public:
  void buildThread();
  void traverseBySuccessor();
  void traverseByPredecessor(); 

// helper methods
private:
  static inline bool visit(Node* T)
  {
    if (T)
    {
      printf("data:%c, left:%c, right:%c\n",
        (char)T->data,
        (T->left!=0) ? (char)T->left->data : '#',
        (T->right!=0) ? (char)T->right->data : '#');
      return true;
    }
    else return false;
  }
}; 

方法定义：

void BinaryTree::makeThread(Node* node)
{
  if (node!=NULL)
  {
    makeThread(node->left);
    if (pre!= NULL)
    {
      if (pre->right==NULL) // 如果前驱节点的右子树为空, 那么把前驱节点的右子树用作线索
      {
        pre->rightTag = true;
        pre->right = node;
      }
      else pre->rightTag = false;
    }
    if (node->left==NULL) // 如果当前结点的左子树为空, 那么把当前结点的左子树用作线索
    {
      node->leftTag = true;
      node->left = pre;
    }
    else node->leftTag = false;
    pre = node;
    makeThread(node->right);
  }
} 

void BinaryTree::traverseBySuccessor()
{
  Node* p = head->left; //first find the root node
  // 亲测表明 如果不使用head哑节点 就要设三道卡, 防止p访问到NULL,
  // 分别在主while处, 第二个visit处和下面的p=p->right处
  while (p!=head)
  {
    while (!p->leftTag)
      p = p->left;
    visit(p); 

    while (p->rightTag && p->right!=head)
    {
      p = p->right;
      visit(p);
    }
    p = p->right;
  }
  cout<<endl;
} 

void BinaryTree::traverseByPredecessor()
{
  Node* p = head->left; //first find the root node
  while (p!=head)
  {
    while (!p->rightTag)
      p = p->right;
    visit(p);
    if (p!=NULL)
    {
      while (p->leftTag && p->left!=head)
      {
        p = p->left;
        visit(p);
      }
      p = p->left;
    }
  }
  cout<<endl;
} 

void BinaryTree::buildThread()
{
  pre = NULL;
  head = new Node('@');
  head->left = root;
  head->right = head;
  makeThread(root);
  // 经过了makeThread过程之后, pre必然指向中序遍历最晚的结点.
  // 把pre的右子树指向head, 就构成了一个双向循环链表
  //
  pre->rightTag = 1;
  pre->right = head;
  pre = NULL;
  Node* p = root;
  /*
   * 在建立前驱线索的时候，最左边的结点没有和head结点连接。要在这里补上
   */
  while (p->left!=NULL)
    p = p->left;
  p->left = head;
} 

感谢阅读，希望能帮助到大家，谢谢大家对本站的支持！