python实现决策树、随机森林的简单原理

本文申明：此文为学习记录过程，中间多处引用大师讲义和内容。

一、概念

决策树（Decision Tree）是一种简单但是广泛使用的分类器。通过训练数据构建决策树，可以高效的对未知的数据进行分类。决策数有两大优点：1）决策树模型可以读性好，具有描述性，有助于人工分析；2）效率高，决策树只需要一次构建，反复使用，每一次预测的最大计算次数不超过决策树的深度。

看了一遍概念后，我们先从一个简单的案例开始，如下图我们样本：

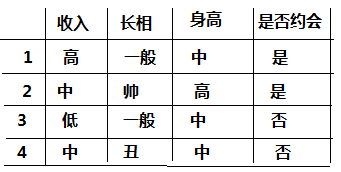
对于上面的样本数据，根据不同特征值我们最后是选择是否约会，我们先自定义的一个决策树，决策树如下图所示：

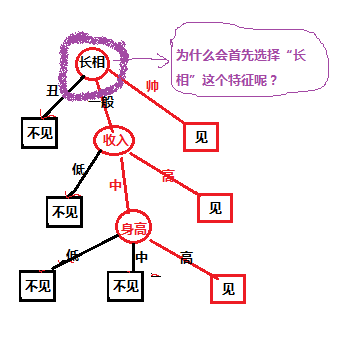
对于上图中的决策树，有个疑问，就是为什么第一个选择是“长相”这个特征，我选择“收入”特征作为第一分类的标准可以嘛？下面我们就对构建决策树选择特征的问题进行讨论；在考虑之前我们要先了解一下相关的数学知识：

信息熵：熵代表信息的不确定性，信息的不确定性越大，熵越大；比如“明天太阳从东方升起”这一句话代表的信息我们可以认为为0；因为太阳从东方升起是个特定的规律，我们可以把这个事件的信息熵约等于0；说白了，信息熵和事件发生的概率成反比：数学上把信息熵定义如下：H(X)＝H(P1，P2，…，Pn)＝-∑P(xi)logP(xi)

互信息：指的是两个随机变量之间的关联程度，即给定一个随机变量后，另一个随机变量不确定性的削弱程度，因而互信息取值最小为0，意味着给定一个随机变量对确定一另一个随机变量没有关系，最大取值为随机变量的熵，意味着给定一个随机变量，能完全消除另一个随机变量的不确定性

现在我们就把信息熵运用到决策树特征选择上，对于选择哪个特征我们按照这个规则进行“哪个特征能使信息的确定性最大我们就选择哪个特征”；比如上图的案例中；

第一步：假设约会去或不去的的事件为Y,其信息熵为H(Y）；

第二步：假设给定特征的条件下，其条件信息熵分别为H(Y|长相)，H(Y|收入)，H(Y|身高)

第三步：分别计算信息增益（互信息）：G(Y,长相) = I(Y,长相) = H(Y)-H(Y|长相) 、G(Y,) = I(Y,长相) = H(Y)-H(Y|长相)等

第四部：选择信息增益最大的特征作为分类特征；因为增益信息大的特征意味着给定这个特征，能很大的消除去约会还是不约会的不确定性；

第五步：迭代选择特征即可；

按以上就解决了决策树的分类特征选择问题，上面的这种方法就是ID3方法，当然还是别的方法如 C4.5;等；

二、决策树的过拟合解决办法

若决策树的度过深的话会出现过拟合现象，对于决策树的过拟合有二个方案：

1.剪枝-先剪枝和后剪纸（可以在构建决策树的时候通过指定深度，每个叶子的样本数来达到剪枝的作用）

2.随机森林 --构建大量的决策树组成森林来防止过拟合；虽然单个树可能存在过拟合，但通过广度的增加就会消除过拟合现象

三、随机森林

随机森林是一个最近比较火的算法，它有很多的优点：

• 在数据集上表现良好
• 在当前的很多数据集上，相对其他算法有着很大的优势
• 它能够处理很高维度（feature很多）的数据，并且不用做特征选择
• 在训练完后，它能够给出哪些feature比较重要
• 训练速度快
• 在训练过程中，能够检测到feature间的互相影响
• 容易做成并行化方法
• 实现比较简单

随机森林顾名思义，是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

上一段决策树代码：

# 花萼长度、花萼宽度，花瓣长度，花瓣宽度
iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica' 

if __name__ == "__main__":
  mpl.rcParams['font.sans-serif'] = [u'SimHei']
  mpl.rcParams['axes.unicode_minus'] = False 

  path = '..\\8.Regression\\iris.data' # 数据文件路径
  data = pd.read_csv(path, header=None)
  x = data[range(4)]
  y = pd.Categorical(data[4]).codes
  # 为了可视化，仅使用前两列特征
  x = x.iloc[:, :2]
  x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.7, random_state=1)
  print y_test.shape 

  # 决策树参数估计
  # min_samples_split = 10：如果该结点包含的样本数目大于10，则(有可能)对其分支
  # min_samples_leaf = 10：若将某结点分支后，得到的每个子结点样本数目都大于10，则完成分支；否则，不进行分支
  model = DecisionTreeClassifier(criterion='entropy')
  model.fit(x_train, y_train)
  y_test_hat = model.predict(x_test)   # 测试数据 

  # 保存
  # dot -Tpng my.dot -o my.png
  # 1、输出
  with open('iris.dot', 'w') as f:
    tree.export_graphviz(model, out_file=f)
  # 2、给定文件名
  # tree.export_graphviz(model, out_file='iris1.dot')
  # 3、输出为pdf格式
  dot_data = tree.export_graphviz(model, out_file=None, feature_names=iris_feature_E, class_names=iris_class,
                  filled=True, rounded=True, special_characters=True)
  graph = pydotplus.graph_from_dot_data(dot_data)
  graph.write_pdf('iris.pdf')
  f = open('iris.png', 'wb')
  f.write(graph.create_png())
  f.close() 

  # 画图
  N, M = 50, 50 # 横纵各采样多少个值
  x1_min, x2_min = x.min()
  x1_max, x2_max = x.max()
  t1 = np.linspace(x1_min, x1_max, N)
  t2 = np.linspace(x2_min, x2_max, M)
  x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
  x_show = np.stack((x1.flat, x2.flat), axis=1) # 测试点
  print x_show.shape 

  # # 无意义，只是为了凑另外两个维度
  # # 打开该注释前，确保注释掉x = x[:, :2]
  # x3 = np.ones(x1.size) * np.average(x[:, 2])
  # x4 = np.ones(x1.size) * np.average(x[:, 3])
  # x_test = np.stack((x1.flat, x2.flat, x3, x4), axis=1) # 测试点 

  cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
  cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
  y_show_hat = model.predict(x_show) # 预测值
  print y_show_hat.shape
  print y_show_hat
  y_show_hat = y_show_hat.reshape(x1.shape) # 使之与输入的形状相同
  print y_show_hat
  plt.figure(facecolor='w')
  plt.pcolormesh(x1, x2, y_show_hat, cmap=cm_light) # 预测值的显示
  plt.scatter(x_test[0], x_test[1], c=y_test.ravel(), edgecolors='k', s=150, zorder=10, cmap=cm_dark, marker='*') # 测试数据
  plt.scatter(x[0], x[1], c=y.ravel(), edgecolors='k', s=40, cmap=cm_dark) # 全部数据
  plt.xlabel(iris_feature[0], fontsize=15)
  plt.ylabel(iris_feature[1], fontsize=15)
  plt.xlim(x1_min, x1_max)
  plt.ylim(x2_min, x2_max)
  plt.grid(True)
  plt.title(u'鸢尾花数据的决策树分类', fontsize=17)
  plt.show()

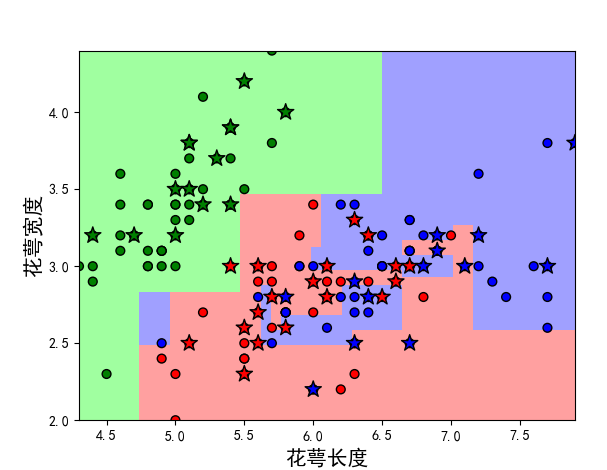
以上就是决策树做分类，但决策树也可以用来做回归，不说直接上代码：

if __name__ == "__main__":
  N =100
  x = np.random.rand(N) *6 -3
  x.sort()
  y = np.sin(x) + np.random.randn(N) *0.05
  x = x.reshape(-1,1)
  print x
  dt = DecisionTreeRegressor(criterion='mse',max_depth=9)
  dt.fit(x,y)
  x_test = np.linspace(-3,3,50).reshape(-1,1)
  y_hat = dt.predict(x_test) 

  plt.plot(x,y,'r*',ms =5,label='Actual')
  plt.plot(x_test,y_hat,'g-',linewidth=2,label='predict')
  plt.legend(loc ='upper left')
  plt.grid()
  plt.show() 

  #比较决策树的深度影响
  depth =[2,4,6,8,10]
  clr = 'rgbmy'
  dtr = DecisionTreeRegressor(criterion='mse')
  plt.plot(x,y,'ko',ms=6,label='Actual')
  x_test = np.linspace(-3,3,50).reshape(-1,1)
  for d,c in zip(depth,clr):
    dtr.set_params(max_depth=d)
    dtr.fit(x,y)
    y_hat = dtr.predict(x_test)
    plt.plot(x_test,y_hat,'-',color=c,linewidth =2,label='Depth=%d' % d)
  plt.legend(loc='upper left')
  plt.grid(b =True)
  plt.show()

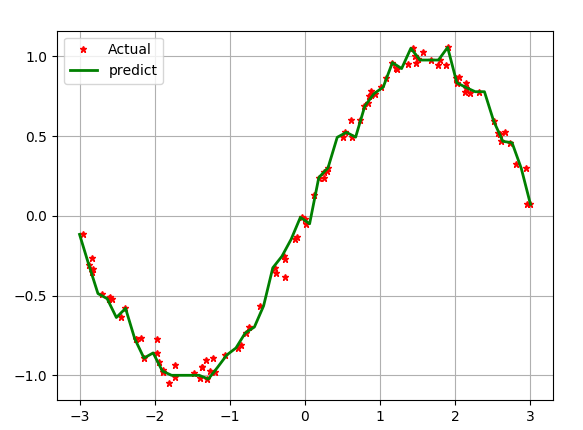
不同深度对回归的 影响如下图：

下面上个随机森林代码

mpl.rcParams['font.sans-serif'] = [u'SimHei'] # 黑体 FangSong/KaiTi
mpl.rcParams['axes.unicode_minus'] = False 

path = 'iris.data' # 数据文件路径
data = pd.read_csv(path, header=None)
x_prime = data[range(4)]
y = pd.Categorical(data[4]).codes
feature_pairs = [[0, 1]]
plt.figure(figsize=(10,9),facecolor='#FFFFFF')
for i,pair in enumerate(feature_pairs):
  x = x_prime[pair]
  clf = RandomForestClassifier(n_estimators=200,criterion='entropy',max_depth=3)
  clf.fit(x,y.ravel())
  N, M =50,50
  x1_min,x2_min = x.min()
  x1_max,x2_max = x.max()
  t1 = np.linspace(x1_min,x1_max, N)
  t2 = np.linspace(x2_min,x2_max, M)
  x1,x2 = np.meshgrid(t1,t2)
  x_test = np.stack((x1.flat,x2.flat),axis =1)
  y_hat = clf.predict(x)
  y = y.reshape(-1)
  c = np.count_nonzero(y_hat == y)
  print '特征：',iris_feature[pair[0]],'+',iris_feature[pair[1]]
  print '\t 预测正确数目：',c
  cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
  cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
  y_hat = clf.predict(x_test)
  y_hat = y_hat.reshape(x1.shape)
  plt.pcolormesh(x1,x2,y_hat,cmap =cm_light)
  plt.scatter(x[pair[0]],x[pair[1]],c=y,edgecolors='k',cmap=cm_dark)
  plt.xlabel(iris_feature[pair[0]],fontsize=12)
  plt.ylabel(iris_feature[pair[1]], fontsize=14)
  plt.xlim(x1_min, x1_max)
  plt.ylim(x2_min, x2_max)
  plt.grid()
plt.tight_layout(2.5)
plt.subplots_adjust(top=0.92)
plt.suptitle(u'随机森林对鸢尾花数据的两特征组合的分类结果', fontsize=18)
plt.show()

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

您可能感兴趣的文章:

• Python实现的随机森林算法与简单总结
• Python决策树和随机森林算法实例详解
• python实现随机森林random forest的原理及方法
• 用Python实现随机森林算法的示例
• 用Python从零实现贝叶斯分类器的机器学习的教程
• Python语言实现机器学习的K-近邻算法
• 机器学习python实战之手写数字识别
• python机器学习之神经网络（一）
• Python机器学习之决策树算法实例详解
• python机器学习之随机森林（七）