Python绘制股票移动均线的实例

1. 前沿

移动均线是股票最进本的指标，本文采用numpy.convolve计算股票的移动均线

2. numpy.convolve

numpy.convolve(a, v, mode='full')

Returns the discrete, linear convolution of two one-dimensional sequences.

The convolution operator is often seen in signal processing, where it models the effect of a linear time-invariant system on a signal [R17]. In probability theory, the sum of two independent random variables is distributed according to the convolution of their individual distributions.

If v is longer than a, the arrays are swapped before computation.

Parameters:

a : (N,) array_like

 First one-dimensional input array.

 v : (M,) array_like

 Second one-dimensional input array.

 mode : {‘full', ‘valid', ‘same'}, optional

 ‘full':

  By default, mode is ‘full'. This returns the convolution at each point of overlap, with an output shape of (N+M-1,). At the end-points of the convolution, the signals do not overlap completely, and boundary effects may be seen.
 ‘same':

  Mode same returns output of length max(M, N). Boundary effects are still visible.
 ‘valid':

  Mode valid returns output of length max(M, N) - min(M, N) + 1. The convolution product is only given for points where the signals overlap completely. Values outside the signal boundary have no effect.

Returns:

out : ndarray

 Discrete, linear convolution of a and v.

计算公式：

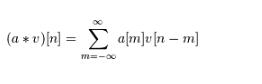
eg:

>>> import numpy as np
>>>
>>> np_list = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
>>>
>>> np_list
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> x = np.convolve(np_list, 2)
>>> x
array([ 2, 4, 6, 8, 10, 12, 14, 16, 18])
>>> x = np.convolve(np_list, [0.5, 0.5])
>>> x
array([ 0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 4.5])

3. 移动均线计算

def moving_average(x, n, type='simple'):
 x = np.asarray(x)
 if type == 'simple':
  weights = np.ones(n)
 else:
  weights = np.exp(np.linspace(-1., 0., n))

 weights /= weights.sum()

 a = np.convolve(x, weights, mode='full')[:len(x)]
 a[:n] = a[n]
 return a

 ma10 = moving_average(close_data, 10, 'simple')
 ma20 = moving_average(close_data, 20, 'simple')

 ax1.plot(data['date'], ma10, color='c', lw=2, label='MA (10)')
 ax1.plot(data['date'], ma20, color='red', lw=2, label='MA (20)')

4. 效果图

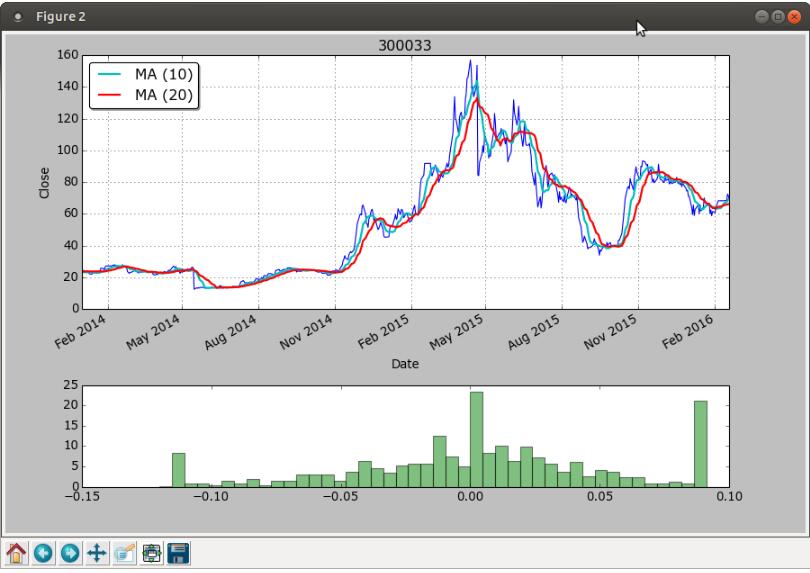
以上这篇Python绘制股票移动均线的实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。