C语言 推理证明带环链表详细过程

目录

• 什么是带环链表：
• 判断链表是否带环：
• 环形链表 I
• 找带环形链表入环的第一个结点：
• 环形链表 II

什么是带环链表：

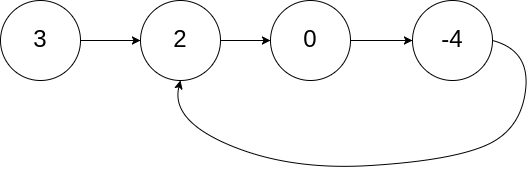
带环链表是链表最后一个结点的指针域不是指向空指针，而是指向链表之前的结点，这样就形成了环状的链表结构。

如图所示：

判断链表是否带环：

那么问题来了，如何判断一个链表是否带环呢？

这里我们再次运用了快慢指针，但是快慢指针又该如何具体设置呢？

• 判断思路：

先定义一个快指针fast，一个慢指针slow。

快指针一定是比慢指针先进环的，当slow进环时，fast指针便开始了追slow指针，当快指针和慢指针相遇的时候，快指针便追上了慢指针，此时就可以判断该链表是有环的，但凡快指针指向空就说明该链表是不带环的。

• 那么快慢指针一次各走几步最合适呢？

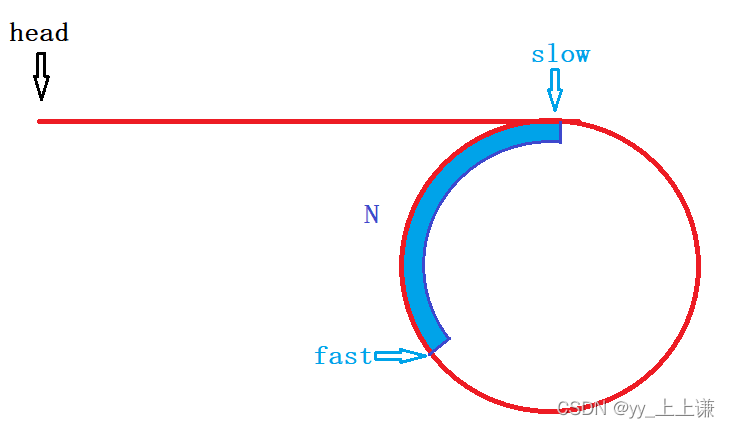
假设slow刚进环时，fast与slow之间的距离为N，环的长度为C。

• 这里我们要多组讨论一下：（先讨论有代表的两组）

1.slow一次走1步，fast一次走2步一定能追上吗？

2.slow一次走1步，fast一次走3步一定能追上吗？

…………………

图为当slow刚进环时，假设fast所在的位置：

1.slow一次走1步，fast一次走2步一定能追上吗？

每次追击，fast与slow之间的距离就缩小1，当距离N缩小为0的时候，便追上了。

N - 1，N - 2，N - 3，……，0

所以这种情况一定能追上。

2.slow一次走1步，fast一次走3步一定能追上吗？

每次追击，fast与slow之间的距离就缩小2，这里要对N进行讨论：

（1）当N为偶数时，N每次缩小2，当距离N缩小为0的时候，便追上了。

N - 2，N - 4，N - 6，……，0

（2）当N为奇数时，N每次缩小2，当距离N缩小为1的时候，下次追击二者距离扔缩小2，此时               fast就会超过slow，距离N变为 -1 ，也就是C - 1，这时又要对C  - 1进行讨论。

• 当C - 1为偶数时就能追上。
• 当C - 1为奇数时就扔会错过，N再次变成C - 1，那么就会永远错过也就永远追不上。

所以这种情况不一定能追上，有可能永远追不上。

3.slow一次走1步，fast一次走4步一定能追上吗？

每次追击，fast与slow之间的距离就缩小3，这里又要对N进行讨论：

（1）当N为3的倍数时，N每次缩小3，当距离N缩小为0的时候，便追上了。

N - 3，N - 6，N - 9，……，0

（2）当N不为3的倍数时，那么fast会与slow错过，至于错过时fast超过slow多少距离还需讨论               （超过的距离取决于一开始N的长度）。

• 当追上后，fast超过slow距离为1时，此时fast追slow追击距离为N即（C - 1），此时又要对C - 1进行上述讨论，即C - 1是否为3的倍数的讨论。
• 当追上后，fast超过slow距离为2时，此时fast追slow追击距离为N即（C - 2），此时又要对C - 2进行上述讨论，即C - 2是否为3的倍数的讨论。

所以这种情况只有当N为3的倍数的时候才能追得上。

综上：能不能追得上取决于两个指针之间的距离N和环的大小C。

下面提供一个结论个人小结：（仅供参考，可能存在局限性）

只要快慢指针的速度差是2的时候，就可能会出现永远追不上的问题。假设fast与slow的速度差为x，那么fast追赶slow一次，他们之间的距离就减少x，途中有可能刚好追上，也有可能错过。当错过的时候，fast在slow前面，这时fast超过slow的距离的取值只可能是在[1 ~ (x - 1)]之间（x取整数）。同时任意一个正整数，假设记作m，（m > x）当m整除一个整数x有余数时，对这个整数m减去[1 ~ (x - 1)]中任意一个值，总能找到一个值x，使得m - x的值能够整除x。所以无论环的长度为多长，假设环的长度为C，总有C减去[1 ~ (x - 1)]中任意一个值，使得C - x能够整除x并且没余数，既然没余数那就是刚好追上的情况。

当fast和slow的速度差为2时，即x = 2的时候，C - x，x属于[1 ~ (x - 1)]，那么C - x就只能是C - 1，那么当C - 1去整除2的时候，如果C - 1为奇数，那么C - 1整除2必然有余数，并且余数为1，下次还是C - 1去整除2，还是会余1，所以这时fast就永远追不上slow。

总结：

设置fast一次走2步，slow一次走1步的时候最保险。 因为快慢指针相距N，每追击一次N就减1，总会减到0，N缩小到0就是追到了。

环形链表 I

环形链表

OJ链接

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

示例 1：

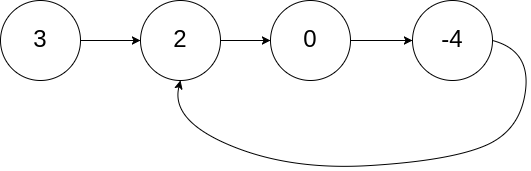
输入：

head = [3,2,0,-4], pos = 1

输出：

true

解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

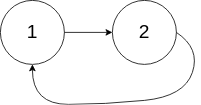
输入：

head = [1,2], pos = 0

输出：

true

解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：

head = [1], pos = -1

输出：

false

解释：链表中没有环。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head)
{
    struct ListNode* fast, *slow;
    fast = slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        return true;
    }

    return false;
}

思路：

运用上述判断环形链表的结论，fast一次走2步，slow每次走1步，只要是环状就一定会追的到。

找带环形链表入环的第一个结点：

接下来更深层次的问题来了，带环链表环的入口该怎么找呢？

以后带环问题通常都用fast一次走2步，slow一次走1步。

当快指针追到慢指针时，假设相遇点为meet，slow指针和fast指针在如图所示的：

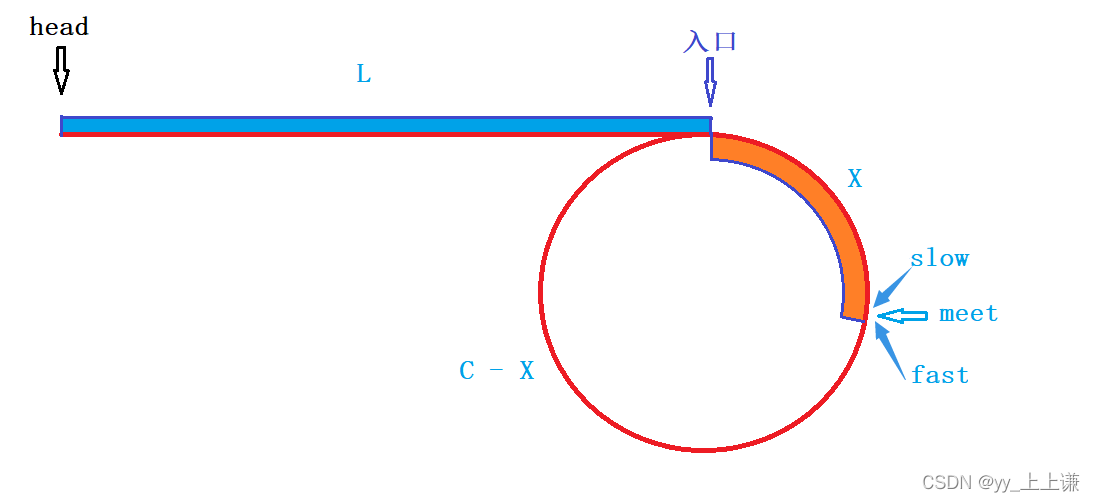
注意：

这里快指针一定是先进环，slow后进环。

slow指针进环后，在走一圈的时间内，一定是会被fast追上的 。

思路：

在是slow指针和fast指针，同时从head头开始走，直到在meet点相遇，又因为fast指针的速度为slow指针速度的二倍，那么就一定满足一个等式关系：

快指针走的距离 = 慢指针走的距离 * 2

还需讨论的是当slow进环时，fast在环内走了多久的问题：

• 当L足够长而C很小时：slow进环时fast可能已经在环内走了好多圈了（假设为n圈）。
• 当L很小而C足够大时：slow进环时fast可能在环内 连一圈还没走。

综合考虑之后再结合上述等式关系变得到下列等式：

L + nC + X = 2 * (L+ X)

化简得：

L = n * C - X

这个公式充分说明了，一个指针从head走，一个指针从相遇点meet走，并且每次都走一步，一     直走下去，它们最终会在环的入口点相遇！！！

环形链表 II

环形链表 II

OJ链接

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改 链表。

示例 1：

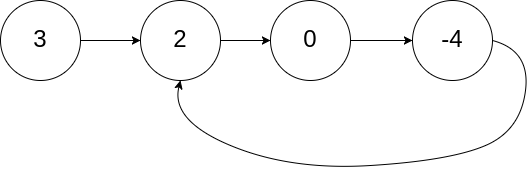
输入：

head = [3,2,0,-4], pos = 1

输出：

返回索引为 1 的链表节点

解释：链表中有一个环，其尾部连接到第二个节点。 示例 2：

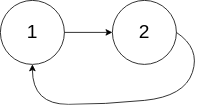
输入：

head = [1,2], pos = 0

输出：

返回索引为 0 的链表节点

解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：

head = [1], pos = -1

输出：

返回 null

解释：链表中没有环。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head)
{
    struct ListNode* fast, *slow;
    slow = fast = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        {
            struct ListNode* meet = slow;
            while(head != meet)
            {
                meet = meet->next;
                head = head->next;
            }
            return meet;
        }
    }
    return NULL;
}

思路1：

先运用上述判断环形链表的结论找到相遇点，再运用上述找环形入口点的结论，就能轻松找到环的入口点。

思路2：

先运用上述判断环形链表的结论找到相遇点，再将相遇点断开，这时就变成了上一篇博客找相交链表公共结点的问题，示意图如下：

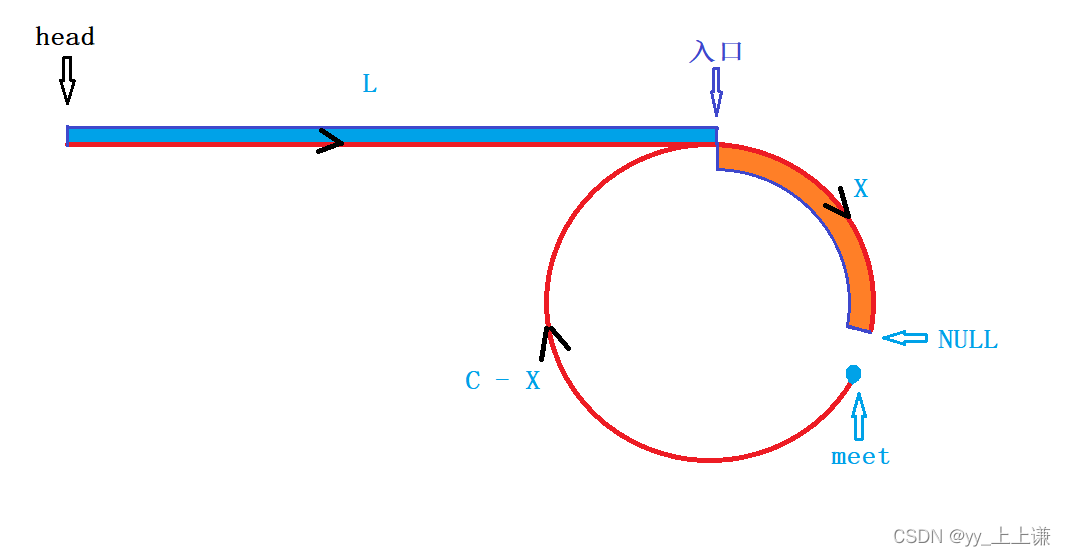
参考代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head)
{
    struct ListNode* fast, *slow;
    slow = fast = head;
    int len1 = 0,len2 = 0;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        {
            struct ListNode* shortList, *longList, *meet, *longTail, *shortTail;
            longList = longTail = head;
            meet = shortList = shortTail = slow->next;
            slow->next = NULL;
            while(shortTail)
            {
                shortTail = shortTail->next;
                len1++;
            }
            while(longTail)
            {
                longTail = longTail->next;
                len2++;
            }
            int gap = abs(len1 - len2);
            if(len1 > len2)
            {
                longList = meet;
                shortList = head;
            }
            while(gap--)
            {
                longList = longList->next;
            }
            while(shortList != longList)
            {
                longList = longList->next;
                shortList = shortList->next;
            }
            return longList;
        }
    }
    return NULL;
}

到此这篇关于C语言 推理证明带环链表详细过程的文章就介绍到这了,更多相关C语言 带环链表内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！