C语言深入探究动态规划之区间DP

2024-10-19 13:05:30

写在前面

之前讲过背包问题，线性DP不知道大家忘了吗，这次是区间DP

石子合并

题意：

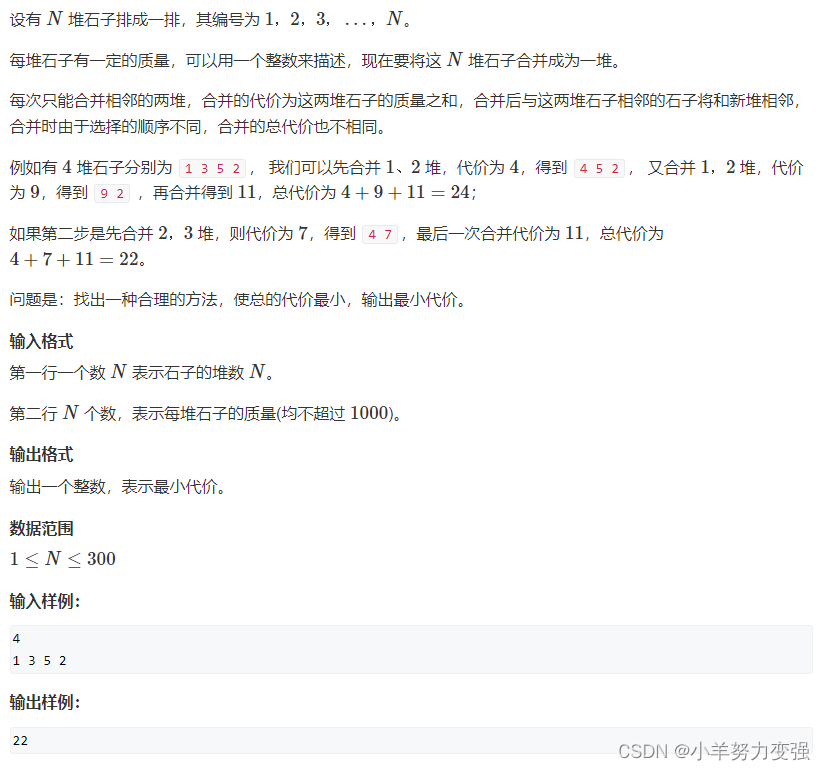
合并 N 堆石子，每次只能合并相邻的两堆石子，求最小代价

解题思路：

关键点：最后一次合并一定是左边连续的一部分和右边连续的一部分进行合并

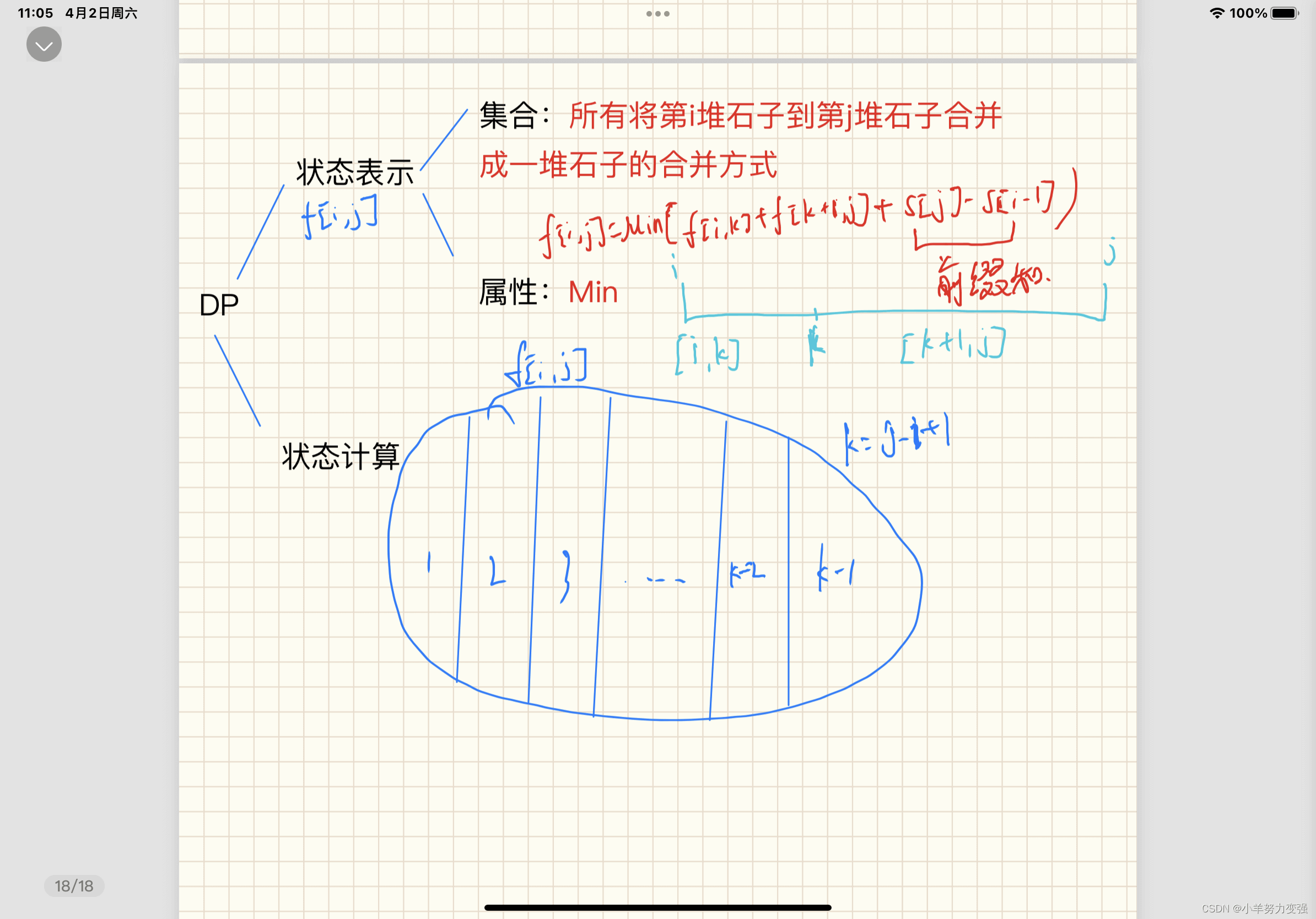
状态表示：f[i][j]表示将 i 到 j 这一段石子合并成一堆的方案的集合，属性 Min

状态计算：（1） i<j 时，f[i][j]=min f[i][k]+f[k+1][j]+s[j]−s[i−1] （2）i=j 时，

f[i][i]=0（合并一堆石子代价为 0）

问题答案： f[1][n]

所有的区间dp问题枚举时，第一维通常是枚举区间长度，并且一般 len = 1 时用来初始化，枚举从 len = 2 开始；第二维枚举起点 i （右端点 j 自动获得，j = i + len - 1）

模板代码如下：

for (int len = 1; len <= n; len++) {         // 区间长度
    for (int i = 1; i + len - 1 <= n; i++) { // 枚举起点
        int j = i + len - 1;                 // 区间终点
        if (len == 1) {
            dp[i][j] = 初始值
            continue;
        }

        for (int k = i; k < j; k++) {        // 枚举分割点，构造状态转移方程
            dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
        }
    }
}

最后总的代码：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 307;

int a[N], s[N];
int f[N][N];

int main() {
    int n;
    cin >> n;

    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        s[i] += s[i - 1] + a[i];
    }

    memset(f, 0x3f, sizeof f);
    // 区间 DP 枚举套路：长度+左端点
    for (int len = 1; len <= n; len ++) { // len表示[i, j]的元素个数
        for (int i = 1; i + len - 1 <= n; i ++) {
            int j = i + len - 1; // 自动得到右端点
            if (len == 1) {
                f[i][j] = 0;  // 边界初始化
                continue;
            }

            for (int k = i; k <= j - 1; k ++) { // 必须满足k + 1 <= j
                f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);
            }
        }
    }

    cout << f[1][n] << endl;

    return 0;
}

到此这篇关于C语言深入探究动态规划之区间DP的文章就介绍到这了,更多相关C语言区间DP内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

C语言矩阵连乘 (动态规划)详解

动态规划法题目描述:给定n个矩阵{A1,A2....An},其中Ai与Ai+1是可以相乘的,判断这n个矩阵通过加括号的方式相乘,使得相乘的次数最少! 以矩阵链ABCD为例按照矩阵链长度递增计算最优值矩阵链长度为1时,分别计算出矩阵链A.B.C.D的最优值矩阵链长度为2时,分别计算出矩阵链AB.BC.CD的最优值矩阵链长度为3时,分别计算出矩阵链ABC.BCD的最优值矩阵链长度为4时,计算出矩阵链ABCD的最优值动归方程: 分析: k为矩阵链断开的位置 d数组存放矩阵链计算的最优值,
C语言动态规划多种背包问题分析讲解

目录写在前面 01背包问题完全背包问题多重背包问题 I 多重背包问题 II 为什么可以这样优化呢一 .二进制与十进制二 .动态规划的时间复杂度估算三 .多重背包分组背包问题写在前面之前讲过简单DP,经典01背包问题,在这我将会把背包问题更深入的讲解,希望能帮助大家更好的理解. 01背包问题 C语言数学问题与简单DP01背包问题详解先回忆一下这个图在这我再将01背包问题代码发一遍,可以用来做对比. 二维: #include<bits/stdc++.h> using name
C语言深入探究动态规划之线性DP

目录写在前面数字三角形最长上升子序列最长上升子序列 II 最长公共子序列写在前面之前讲过背包问题,不知道大家忘了吗,如果忘了可以点这里,这次是线性DP 数字三角形状态表示:f[i,j],到点i,j的最大路径状态计算:f[i,j] = MAX(f[i-1,j-1]+a[i,j],f[i-1,j]+a[i,j]) 看图,以例题为例,将它看成五行五列的三角形,每个点都可以用坐标表示.那么我们可以得知到一个数的最大路径要么来自左上,要么来自右上.左上的数用f[i-1,j-1]表示,右上的
C语言动态规划点杀dp算法LeetCode炒股习题案例解析

目录概念性质典型特征实战论证算法实现优化概念说到动态规划,什么是动态规划? 动态规划(英语:Dynamic programming,简称 dp)通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法.动态规划常常适用于有重叠子问题和最优子结构性质的问题. 看着这么复杂哈,其实总结出来就是大事化小,拆分成小问题但是这些小问题和原问题是同质的,动规致力于解决每一个子问题,减少计算,其实和递归思想,分治法有些类似,斐波那契数列就可以看做入门级的经典动规问题这里引用一个网上流行的例
C语言动态规划之背包问题详解

01背包问题给定n种物品,和一个容量为C的背包,物品i的重量是w[i],其价值为v[i].问如何选择装入背包的物品,使得装入背包中的总价值最大?(面对每个武平,只能有选择拿取或者不拿两种选择,不能选择装入某物品的一部分,也不能装入物品多次) 声明一个数组f[n][c]的二维数组,f[i][j]表示在面对第i件物品,且背包容量为j时所能获得的最大价值. 根据题目要求进行打表查找相关的边界和规律根据打表列写相关的状态转移方程用程序实现状态转移方程真题演练: 一个旅行者有一个最多能装M公斤的背
C语言使用DP动态规划思想解最大K乘积与乘积最大问题

最大K乘积问题设I是一个n位十进制整数.如果将I划分为k段,则可得到k个整数.这k个整数的乘积称为I的一个k乘积.试设计一个算法,对于给定的I和k,求出I的最大k乘积. 编程任务: 对于给定的I 和k,编程计算I 的最大k 乘积. 需求输入: 输入的第1 行中有2个正整数n和k.正整数n是序列的长度:正整数k是分割的段数.接下来的一行中是一个n位十进制整数.(n<=10) 需求输出: 计算出的最大k乘积. 解题思路:DP 设w(h,k) 表示: 从第1位到第K位所组成的十进制数,设m(i,j)
C语言深入探究动态规划之区间DP

目录写在前面石子合并写在前面之前讲过背包问题,线性DP不知道大家忘了吗,这次是区间DP 石子合并题意: 合并 N 堆石子,每次只能合并相邻的两堆石子,求最小代价解题思路: 关键点:最后一次合并一定是左边连续的一部分和右边连续的一部分进行合并状态表示:f[i][j]表示将 i 到 j 这一段石子合并成一堆的方案的集合,属性 Min 状态计算: (1) i<j 时,f[i][j]=min f[i][k]+f[k+1][j]+s[j]−s[i−1] (2)i=j 时, f[i][i]=0
C语言深入理解动态规划之计数类DP

目录写在前面石子合并写在前面之前讲过背包问题,线性DP,区间DP,不知道大家忘了吗,这次是计数类DP 石子合并老规矩,先画图. 思路:把1,2,3, … n分别看做n个物体的体积,这n个物体均无使用次数限制,问恰好能装满总体积为n的背包的总方案数(完全背包问题变形) 初值问题: 求最大值时,当都不选时,价值显然是 0 而求方案数时,当都不选时,方案数是 1(即前 i 个物品都不选的情况也是一种方案),所以需要初始化为 1 即:for (int i = 0; i <= n; i ++)
C语言深入理解动态规划之计数类DP

目录写在前面石子合并写在前面之前讲过背包问题,线性DP,区间DP,不知道大家忘了吗,这次是计数类DP 石子合并老规矩,先画图. 思路:把1,2,3, … n分别看做n个物体的体积,这n个物体均无使用次数限制,问恰好能装满总体积为n的背包的总方案数(完全背包问题变形) 初值问题: 求最大值时,当都不选时,价值显然是 0 而求方案数时,当都不选时,方案数是 1(即前 i 个物品都不选的情况也是一种方案),所以需要初始化为 1 即:for (int i = 0; i <= n; i ++)
C语言深入探究斐波那契数列

目录一.递归思想二.空间换时间三.动态规划四.通项公式五.矩阵快速幂六.总结本文章参考leetcode斐波那契数官方题解斐波那契的边界条件是 F(0)=0 和 F(1)=1.当 n>1 时,每一项的和都等于前两项的和,因此有如下递推关系:F(n)=F(n-1)+F(n-2) 一.递归思想递归的思想是把一个大型复杂问题层层转化为一个与原问题规模更小的问题,问题被拆解成子问题后,递归调用继续进行,直到子问题无需进一步递归就可以解决的地步为止. #include<stdio.h&g
C语言深入探究sizeof与整型数据存储及数据类型取值范围

目录 1.关键字sizeof 2.整型数据存储深入 3.数据类型取值范围深入 1.关键字sizeof sizeof 与 strlen 是我们日常打代码时经常使用到的两个“工具”.前者是求变量或者类型的大小(单位为字节),后者是求某一字符串的长度.我们很容易产生这样一个误解,即把 sizeof 和 strlen 归为函数一类.事实上 sizeof 并不是一个函数,它是一个操作符.关键字.我们通过一段代码证明它不是函数: #include <stdio.h> int main() { int n
C语言深入探究栈的原理

栈压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶. 出栈:栈的删除操作叫做出栈.出数据也在栈顶. 栈的实现栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些.因为数组在尾上插入数据的代价比较小.如下图: 下面用顺序表(数组)来实现栈: 建立一个顺序表结构: typedef int STDataType; typedef struct Stack { STDataType* a; int top; //表示栈顶 int capacity;//表示容量,当容量满时,扩容
C语言深入探究函数的溯源

目录一.函数的由来二.模块化程序设计三.C 语言中的模块化四.面向过程的程序设计五.声名和定义六.小结一.函数的由来二.模块化程序设计三.C 语言中的模块化四.面向过程的程序设计面向过程是一种以过程为中心的编程思想首先将复杂的问题分解为一个个容易解决的问题分解过后的问题可以按照步骤一步步完成函数是面向过程在 C 语言中的体现解决问题的每个步骤可以用函数来实现五.声名和定义声明的意义在于告诉编译器程序单元的存在定义则明确指示程序单元的意义 C 语言中通过 ext
C语言深入探究水仙花数与变种水仙花数代码

目录 1.水仙花 1.1先看代码 1.2大体逻辑 2.变种水仙花数 2.1先看代码 2.2代码剖析 1.水仙花题目: 1.1先看代码 #include <stdio.h> int main() { int i = 0; int count = 0; for (i = 100; i<= 999; i++) { int a = i / 100; int b = (i % 100)/10; int c = (i % 100)%10; if (i == a * a * a + b * b *
C语言深入探究直接插入排序与希尔排序使用案例讲解

目录一.直接插入排序 1.1直接插入排序引入 1.2直接插入排序的核心思想与算法分析 1.3实例说明 1.4直接插入排序代码实现 1.5直接插入排序性能分析二.希尔排序 2.1希尔排序引入 2.2希尔排序的核心思想与算法分析 2.3实例说明 2.4希尔排序代码实现 2.5希尔排序性能分析一.直接插入排序 1.1直接插入排序引入排序是我们生活中经常会面对的问题,以打扑克牌为例,你摸的手牌肯定是杂乱的,你一定会将小牌移动到大牌的左面,大牌移动到小牌的右面,这样顺序就算理好了.这里我们的理牌方

C语言 深入探究动态规划之区间DP

目录

写在前面

石子合并

相关推荐

随机推荐

C语言深入探究动态规划之区间DP