p5.js临摹旋转爱心

运用p5.js临摹旋转爱心，供大家参考，具体内容如下

原图

我的临摹

效果不错的样子，让我们看看实现过程。

第一步、分析原图GIF

因为原图中旋转速度较快，无法用肉眼直观地找到规律。所以我把gif分解，共90帧，一帧一帧的寻找旋转规律。

从上往下顺序，第一层到第六层。从简单的说起。
第六层：逆时针匀速旋转一圈。
第五层：先逆时针旋转α，速度由v1变为0。再顺时针旋转180°+2α，速度由0变为v2，再变为0。最后逆时针旋转α，速度由0变为v1。（观察原图，我将α设为30°0）
第四层：先逆时针旋转α，再顺时针旋转3×180°+2α，最后逆时针旋转α。速度规律与第五层相同。
第三层：先逆时针旋转α，再顺时针旋转5×180°+2α，最后逆时针旋转α。速度规律与第五层相同。
第二层：先逆时针旋转α，再顺时针旋转7×180°+2α，最后逆时针旋转α。速度规律与第五层相同。
第一层：先逆时针旋转α，再顺时针旋转9×180°+2α，最后逆时针旋转α。速度规律与第五层相同。
（注：使用时记得转化为弧度制。）

第二步、绘制基本形状

首先创建画布，设置背景色

function setup() {
  createCanvas(windowWidth, windowHeight,WEBGL);
}

function draw() {
background(220);
}

绘制第一层立方体

值得注意的是translate()函数使用的是偏移量，而不是坐标值。

function drawHeart1(BoxSize,posX,posY,posZ,r,g,b)  //第一排方块
{
fill(r,g,b);
translate(posX-(10/9)*BoxSize,posY,posZ);
box(BoxSize);
translate(-(10/9)*BoxSize,0,0);
box(BoxSize);
translate(3*(10/9)*BoxSize,0,0);
box(BoxSize);
translate((10/9)*BoxSize,0,0);
box(BoxSize);
translate(0,0,(10/9)*BoxSize);
box(BoxSize);
translate(-(10/9)*BoxSize,0,0);
box(BoxSize);
translate(-2*(10/9)*BoxSize,0,0);
box(BoxSize);
translate(-(10/9)*BoxSize,0,0);
box(BoxSize);
}

在draw（）函数中，添加代码。
drawHearts（）中第一个参数是立方体的边长，第二到第四个参数是XYZ轴的偏移量，最后三个为立方体颜色RGB值。

push();
translate(0,0);
drawHeart1(40*size1,0,-2*40*10/9,-20,251,68,104);
pop();

以此类推画出其余五层的立方体。

效果图如上（此处调整了一下相机位置）

第三步、旋转

在之前绘制每一层时，要注意物体的X、Z为0，因为rotateY()函数绕Y轴旋转，否则每一层在旋转时不是以绕其中心旋转。

第六层的旋转

①设置旋转角度变量

②在draw()函数中关于第六层代码。其中theta6-=360*PI/180/90表示一帧旋转的弧度增量。

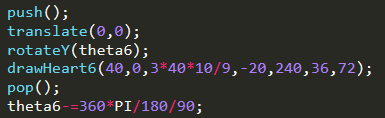
②在draw()函数中关于第五层代码。

③RotateCubes5()函数。第一个参数表示逆时针旋转角度，第二个参数表示顺时针旋转角度的二分之一，第四、五、六个参数用来判断旋转时帧的范围，并用于计算旋转角度。
以第一个if语句为例
在第一帧到第f1帧时，theta5减小，即实现逆时针绕Y轴旋转。其中，frameCount表示当前第几帧。frameCount%90，因为原图有90帧。（f1-frameCount%90）* delta1 * PI *180/Summation（0，f1-1）实现1到f1范围内当前帧数越大，旋转弧度越小。

function RotateCubes5(delta1,delta2,f1,f2,f3){
 if(frameCount%90>=1&&frameCount%90<=f1)
 {
 theta5-=(f1-frameCount%90)*delta1*PI/180/Summation(0,f1-1);
 }
 if(frameCount%90>=f1+1&&frameCount%90<=f2)
 {
 theta5+=(frameCount%90-f1-1)*delta2*PI/180/Summation(0,f2-f1-1);
 }
 if(frameCount%90>=f2+1&&frameCount%90<=f3)
 {
 theta5+=(f3-frameCount%90)*delta2*PI/180/Summation(0,f2-f1-1);
 }
 if(frameCount%90>=f3+1&&frameCount%90<=89)
 {
 theta5-=(frameCount%90-f3-1)*delta1*PI/180/Summation(0,f1-1);
 }
 if(frameCount%90==0)
 {
    theta5-=(90-f3-1)*delta1*PI/180/Summation(0,f1-1);
 }
  return theta5;
}

③Summation()函数，即高斯求和。

function Summation(n1,n2)
{
 return (n1+n2)*(n2-n1+1)/2;
}

第一到四层的旋转
第一到四层的旋转与第五层一致，修改传入参数即可。
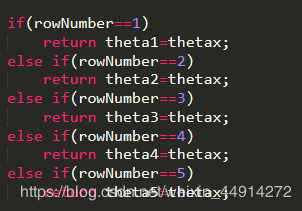
其实RotateCubes()的内容是一致的，最后返回一个theta。但当我为theta赋值后return（如下图），产生效果发生错误 ，分配数据发生错误。第一次接触p5.js，感觉代码写得比较冗余，后续学习中优化。

以上，即完成了对原图的临摹。

拓展作品

让立方体的大小随帧数变化，90帧一循环。

随帧数增加，深粉立方体变小，浅粉立方体变大。并在一瞬间，深粉立方体和浅粉立方体大小相同，形成一个完整的爱心。

if(frameCount%200>=0&&frameCount%200<=99)  //扩展作品2
{
 size1=frameCount%100*0.02;
  size2=(100-frameCount%100)*0.02;
  size3=frameCount%100*0.02;
  size4=(100-frameCount%100)*0.02;
  size5=frameCount%100*0.02;
  size6=(100-frameCount%100)*0.02;
}
if(frameCount%200>=100&&frameCount%200<=199)
{
  size1=(100-frameCount%100)*0.02;
  size2=frameCount%100*0.02;
  size3=(100-frameCount%100)*0.02;
  size4=frameCount%100*0.02;
  size5=(100-frameCount%100)*0.02;
  size6=frameCount%100*0.02;
}

体会：

三维图形比起二维图像要多一个z参数，所以在排布位置的时候难度增大，且translate（）函数的参数是偏移量，又为图形绘制增加了难度。

本GIF又一难点在于运动规律不能用肉眼直接获得，需要把GIF分解到每一帧，逐帧观察。运动规律相对复杂，且每一层运动规律都不同，需要控制的变量较多。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。