Python统计学一数据的概括性度量详解

一、数据的概括性度量

1、统计学概括：

统计学是应用数学的一个分支，主要通过利用概率论建立数学模型，收集所观察系统的数据，进行量化的分析、总结，并进而进行推断和预测，为相关决策提供依据和参考。统计学主要又分为描述统计学和推断统计学。给定一组数据，统计学可以摘要并且描述这份数据，这个用法称作为描述统计学。另外，观察者以数据的形态建立出一个用以解释其随机性和不确定性的数学模型，以之来推论研究中的步骤及母体，这种用法被称做推论统计学。

2、数据的概括性度量：

1）集中趋势的度量：

众数：众数(Mode)，是一组数据中出现次数最多的数值，叫众数，有时众数在一组数中有好几个。用M表示。

中位数：中位数(Median)是指将数据按大小顺序排列起来，形成一个数列，居于数列中间位置的那个数据。中位数用Me表示。计算公式：

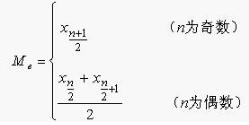
四分位数：四分位数（Quartile）把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分位数。QL=下四分位数，即第25百分位数（ n / 4）；QU=上四分位数，即第75百分位数（ 3n / 4）。

平均数：算术平均数（arithmetic mean）算术平均数是指资料中各观测值的总和除以观测值个数所得的商，简称平均数或均数。

2）离散趋势的度量：

四分位差：四分位差(quartile deviation)，也称为内距或四分间距(inter-quartile range)，它是上四分位数(QU，即位于75%)与下四分位数(QL，即位于25%)的差。

极差：全距(Range)，又称极差，是用来表示统计资料中的变异量数(measures of variation)，其最大值与最小值之间的差距

方差：方差（variance)（样本方差）是各个数据分别与其平均数之差的平方的和的平均数，通常以σ2表示，方差的计算公式为：

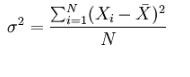
标准差：标准差 (Standard Deviation)，也称均方差（Mean square error）， 。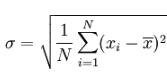

离散系数：离散系数又称变异系数，CV(Coefficient of Variance)表示。CV(Coefficient of Variance)：标准差与均值的比值。离散系数越小，数据的离散程度就越小，反之，亦然。

3）偏度与峰度的度量：

偏态系数：偏度(Skewness)亦称偏态、偏态系数，偏度是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。Sk>0时，分布呈正偏态（右偏），Sk<0时，分布呈负偏态（左偏）。

峰态系数：（Kurtosis)峰度系数是用来反映频数分布曲线顶端尖峭或扁平程度的指标。在正态分布情况下，峰度系数值是3。>3的峰度系数说明观察量更集中，有比正态分布更短的尾部；<3的峰度系数说明观测量不那么集中，有比正态分布更长的尾部，类似于矩形的均匀分布。峰度系数的标准误用来判断分布的正态性。峰度系数与其标准误的比值用来检验正态性。如果该比值绝对值大于2，将拒绝正态性。

3、Python代码实现：

<span style="font-family:Microsoft YaHei;font-size:12px;">#以下代码基于Python3.5环境编写
import numpy as np
import stats as sts
scores = [31, 24, 23, 25, 14, 25, 13, 12, 14, 23,
     32, 34, 43, 41, 21, 23, 26, 26, 34, 42,
     43, 25, 24, 23, 24, 44, 23, 14, 52,32,
     42, 44, 35, 28, 17, 21, 32, 42, 12, 34]
#集中趋势的度量
print('求和：',np.sum(scores))
print('个数：',len(scores))
print('平均值:',np.mean(scores))
print('中位数:',np.median(scores))
print('众数:',sts.mode(scores))
print('上四分位数',sts.quantile(scores,p=0.25))
print('下四分位数',sts.quantile(scores,p=0.75))
#离散趋势的度量
print('最大值:',np.max(scores))
print('最小值:',np.min(scores))
print('极差:',np.max(scores)-np.min(scores))
print('四分位差',sts.quantile(scores,p=0.75)-sts.quantile(scores,p=0.25))
print('标准差:',np.std(scores))
print('方差:',np.var(scores))
print('离散系数:',np.std(scores)/np.mean(scores))
#偏度与峰度的度量
print('偏度:',sts.skewness(scores))
print('峰度:',sts.kurtosis(scores))</span>

以上这篇Python统计学一数据的概括性度量详解就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。