如何利用Javascript生成平滑曲线详解

目录

• 前言
• 贝塞尔曲线简介
• 二次贝塞尔曲线
• 三次贝塞尔曲线
• 贝塞尔曲线计算函数
• 拟合算法
• 附录：Vector2D相关的代码
• 总结

前言

平滑曲线生成是一个很实用的技术

很多时候，我们都需要通过绘制一些折线，然后让计算机平滑的连接起来，

先来看下最终效果(红色为我们输入的直线，蓝色为拟合过后的曲线) 首尾可以特殊处理让图形看起来更好：）

实现思路是利用贝塞尔曲线进行拟合

贝塞尔曲线简介

贝塞尔曲线（英语：Bézier curve）是计算机图形学中相当重要的参数曲线。

二次贝塞尔曲线

二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B（t）追踪：

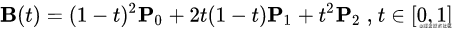
三次贝塞尔曲线

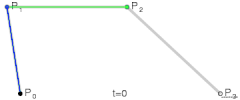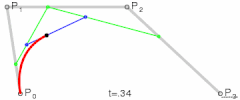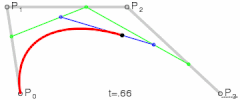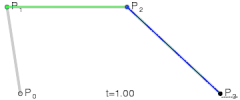
对于三次曲线，可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2，和由二次曲线描述的点R0、R1所建构

贝塞尔曲线计算函数

根据上面的公式我们可有得到计算函数

二阶

  /**
   *
   *
   * @param {number} p0
   * @param {number} p1
   * @param {number} p2
   * @param {number} t
   * @return {*}
   * @memberof Path
   */
  bezier2P(p0: number, p1: number, p2: number, t: number) {
    const P0 = p0 * Math.pow(1 - t, 2);
    const P1 = p1 * 2 * t * (1 - t);
    const P2 = p2 * t * t;
    return P0 + P1 + P2;
  }

    /**
   *
   *
   * @param {Point} p0
   * @param {Point} p1
   * @param {Point} p2
   * @param {number} num
   * @param {number} tick
   * @return {*}  {Point}
   * @memberof Path
   */
  getBezierNowPoint2P(
      p0: Point,
      p1: Point,
      p2: Point,
      num: number,
      tick: number,
  ): Point {
    return {
      x: this.bezier2P(p0.x, p1.x, p2.x, num * tick),
      y: this.bezier2P(p0.y, p1.y, p2.y, num * tick),
    };
  }

    /**
   * 生成二次方贝塞尔曲线顶点数据
   *
   * @param {Point} p0
   * @param {Point} p1
   * @param {Point} p2
   * @param {number} [num=100]
   * @param {number} [tick=1]
   * @return {*}
   * @memberof Path
   */
  create2PBezier(
      p0: Point,
      p1: Point,
      p2: Point,
      num: number = 100,
      tick: number = 1,
  ) {
    const t = tick / (num - 1);
    const points = [];
    for (let i = 0; i < num; i++) {
      const point = this.getBezierNowPoint2P(p0, p1, p2, i, t);
      points.push({x: point.x, y: point.y});
    }
    return points;
  }

三阶

/**
   * 三次方塞尔曲线公式
   *
   * @param {number} p0
   * @param {number} p1
   * @param {number} p2
   * @param {number} p3
   * @param {number} t
   * @return {*}
   * @memberof Path
   */
  bezier3P(p0: number, p1: number, p2: number, p3: number, t: number) {
    const P0 = p0 * Math.pow(1 - t, 3);
    const P1 = 3 * p1 * t * Math.pow(1 - t, 2);
    const P2 = 3 * p2 * Math.pow(t, 2) * (1 - t);
    const P3 = p3 * Math.pow(t, 3);
    return P0 + P1 + P2 + P3;
  }

    /**
   * 获取坐标
   *
   * @param {Point} p0
   * @param {Point} p1
   * @param {Point} p2
   * @param {Point} p3
   * @param {number} num
   * @param {number} tick
   * @return {*}
   * @memberof Path
   */
  getBezierNowPoint3P(
      p0: Point,
      p1: Point,
      p2: Point,
      p3: Point,
      num: number,
      tick: number,
  ) {
    return {
      x: this.bezier3P(p0.x, p1.x, p2.x, p3.x, num * tick),
      y: this.bezier3P(p0.y, p1.y, p2.y, p3.y, num * tick),
    };
  }

    /**
   * 生成三次方贝塞尔曲线顶点数据
   *
   * @param {Point} p0 起始点  { x : number, y : number}
   * @param {Point} p1 控制点1 { x : number, y : number}
   * @param {Point} p2 控制点2 { x : number, y : number}
   * @param {Point} p3 终止点  { x : number, y : number}
   * @param {number} [num=100]
   * @param {number} [tick=1]
   * @return {Point []}
   * @memberof Path
   */
  create3PBezier(
      p0: Point,
      p1: Point,
      p2: Point,
      p3: Point,
      num: number = 100,
      tick: number = 1,
  ) {
    const pointMum = num;
    const _tick = tick;
    const t = _tick / (pointMum - 1);
    const points = [];
    for (let i = 0; i < pointMum; i++) {
      const point = this.getBezierNowPoint3P(p0, p1, p2, p3, i, t);
      points.push({x: point.x, y: point.y});
    }
    return points;
  }

拟合算法

问题在于如何得到控制点，我们以比较简单的方法

取 p1-pt-p2的角平分线 c1c2垂直于该条角平分线 c2为p2的投影点取短边作为c1-pt c2-pt的长度对该长度进行缩放 这个长度可以大概理解为曲线的弯曲程度

ab线段 这里简单处理 只使用了二阶的曲线生成 -> 🌈 这里可以按照个人想法处理

bc线段使用abc计算出来的控制点c2和bcd计算出来的控制点c3 以此类推

  /**
   * 生成平滑曲线所需的控制点
   *
   * @param {Vector2D} p1
   * @param {Vector2D} pt
   * @param {Vector2D} p2
   * @param {number} [ratio=0.3]
   * @return {*}
   * @memberof Path
   */
  createSmoothLineControlPoint(
      p1: Vector2D,
      pt: Vector2D,
      p2: Vector2D,
      ratio: number = 0.3,
  ) {
    const vec1T: Vector2D = vector2dMinus(p1, pt);
    const vecT2: Vector2D = vector2dMinus(p1, pt);
    const len1: number = vec1T.length;
    const len2: number = vecT2.length;
    const v: number = len1 / len2;
    let delta;
    if (v > 1) {
      delta = vector2dMinus(
          p1,
          vector2dPlus(pt, vector2dMinus(p2, pt).scale(1 / v)),
      );
    } else {
      delta = vector2dMinus(
          vector2dPlus(pt, vector2dMinus(p1, pt).scale(v)),
          p2,
      );
    }
    delta = delta.scale(ratio);
    const control1: Point = {
      x: vector2dPlus(pt, delta).x,
      y: vector2dPlus(pt, delta).y,
    };
    const control2: Point = {
      x: vector2dMinus(pt, delta).x,
      y: vector2dMinus(pt, delta).y,
    };
    return {control1, control2};
  }

    /**
   * 平滑曲线生成
   *
   * @param {Point []} points
   * @param {number} ratio
   * @return {*}
   * @memberof Path
   */
  createSmoothLine(points: Point[], ratio: number = 0.3) {
    const len = points.length;
    let resultPoints = [];
    const controlPoints = [];
    if (len < 3) return;
    for (let i = 0; i < len - 2; i++) {
      const {control1, control2} = this.createSmoothLineControlPoint(
          new Vector2D(points[i].x, points[i].y),
          new Vector2D(points[i + 1].x, points[i + 1].y),
          new Vector2D(points[i + 2].x, points[i + 2].y),
          ratio,
      );
      controlPoints.push(control1);
      controlPoints.push(control2);
      let points1;
      let points2;

      // 首端控制点只用一个
      if (i === 0) {
        points1 = this.create2PBezier(points[i], control1, points[i + 1], 50);
      } else {
        console.log(controlPoints);
        points1 = this.create3PBezier(
            points[i],
            controlPoints[2 * i - 1],
            control1,
            points[i + 1],
            50,
        );
      }
      // 尾端部分
      if (i + 2 === len - 1) {
        points2 = this.create2PBezier(
            points[i + 1],
            control2,
            points[i + 2],
            50,
        );
      }

      if (i + 2 === len - 1) {
        resultPoints = [...resultPoints, ...points1, ...points2];
      } else {
        resultPoints = [...resultPoints, ...points1];
      }
    }
    return resultPoints;
  }

案例代码

    const input = [
        { x: 0, y: 0 },
        { x: 150, y: 150 },
        { x: 300, y: 0 },
        { x: 400, y: 150 },
        { x: 500, y: 0 },
        { x: 650, y: 150 },
    ]
    const s = path.createSmoothLine(input);
    let ctx = document.getElementById('cv').getContext('2d');
    ctx.strokeStyle = 'blue';
    ctx.beginPath();
    ctx.moveTo(0, 0);
    for (let i = 0; i < s.length; i++) {
        ctx.lineTo(s[i].x, s[i].y);
    }
    ctx.stroke();
    ctx.beginPath();
    ctx.moveTo(0, 0);
    for (let i = 0; i < input.length; i++) {
        ctx.lineTo(input[i].x, input[i].y);
    }
    ctx.strokeStyle = 'red';
    ctx.stroke();
    document.getElementById('btn').addEventListener('click', () => {
        let app = document.getElementById('app');
        let index = 0;
        let move = () => {
            if (index < s.length) {
                app.style.left = s[index].x - 10 + 'px';
                app.style.top = s[index].y - 10 + 'px';
                index++;
                requestAnimationFrame(move)
            }
        }
        move()
    })

附录：Vector2D相关的代码

/**
 *
 *
 * @class Vector2D
 * @extends {Array}
 */
class Vector2D extends Array {
  /**
   * Creates an instance of Vector2D.
   * @param {number} [x=1]
   * @param {number} [y=0]
   * @memberof Vector2D
   * */
  constructor(x: number = 1, y: number = 0) {
    super();
    this.x = x;
    this.y = y;
  }

  /**
   *
   * @param {number} v
   * @memberof Vector2D
   */
  set x(v) {
    this[0] = v;
  }

  /**
   *
   * @param {number} v
   * @memberof Vector2D
   */
  set y(v) {
    this[1] = v;
  }

  /**
   *
   *
   * @readonly
   * @memberof Vector2D
   */
  get x() {
    return this[0];
  }

  /**
   *
   *
   * @readonly
   * @memberof Vector2D
   */
  get y() {
    return this[1];
  }

  /**
   *
   *
   * @readonly
   * @memberof Vector2D
   */
  get length() {
    return Math.hypot(this.x, this.y);
  }

  /**
   *
   *
   * @readonly
   * @memberof Vector2D
   */
  get dir() {
    return Math.atan2(this.y, this.x);
  }

  /**
   *
   *
   * @return {*}
   * @memberof Vector2D
   */
  copy() {
    return new Vector2D(this.x, this.y);
  }

  /**
   *
   *
   * @param {*} v
   * @return {*}
   * @memberof Vector2D
   */
  add(v) {
    this.x += v.x;
    this.y += v.y;
    return this;
  }

  /**
   *
   *
   * @param {*} v
   * @return {*}
   * @memberof Vector2D
   */
  sub(v) {
    this.x -= v.x;
    this.y -= v.y;
    return this;
  }

  /**
   *
   *
   * @param {*} a
   * @return {Vector2D}
   * @memberof Vector2D
   */
  scale(a) {
    this.x *= a;
    this.y *= a;
    return this;
  }

  /**
   *
   *
   * @param {*} rad
   * @return {*}
   * @memberof Vector2D
   */
  rotate(rad) {
    const c = Math.cos(rad);
    const s = Math.sin(rad);
    const [x, y] = this;

    this.x = x * c + y * -s;
    this.y = x * s + y * c;

    return this;
  }

  /**
   *
   *
   * @param {*} v
   * @return {*}
   * @memberof Vector2D
   */
  cross(v) {
    return this.x * v.y - v.x * this.y;
  }

  /**
   *
   *
   * @param {*} v
   * @return {*}
   * @memberof Vector2D
   */
  dot(v) {
    return this.x * v.x + v.y * this.y;
  }

  /**
   * 归一
   *
   * @return {*}
   * @memberof Vector2D
   */
  normalize() {
    return this.scale(1 / this.length);
  }
}

/**
 * 向量的加法
 *
 * @param {*} vec1
 * @param {*} vec2
 * @return {Vector2D}
 */
function vector2dPlus(vec1, vec2) {
  return new Vector2D(vec1.x + vec2.x, vec1.y + vec2.y);
}

/**
 * 向量的减法
 *
 * @param {*} vec1
 * @param {*} vec2
 * @return {Vector2D}
 */
function vector2dMinus(vec1, vec2) {
  return new Vector2D(vec1.x - vec2.x, vec1.y - vec2.y);
}

export {Vector2D, vector2dPlus, vector2dMinus};

总结

到此这篇关于如何利用Javascript生成平滑曲线的文章就介绍到这了,更多相关JS生成平滑曲线内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！