数据结构之树的概念详解
数据结构树简介
一、树简介
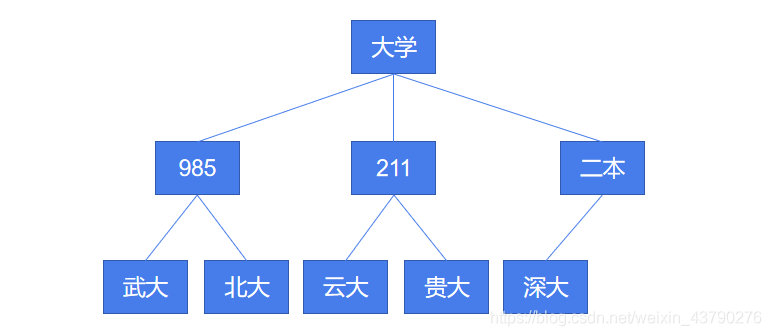
树(Tree)是一种抽象的数据结构,是一个数据的集合,集合中的数据组成了一个树状结构。例如上图,看起来像一棵倒挂的树,根朝上叶朝下。
树是由n(n>=0)个节点组成的具有层次关系的数据集合。当 n=0 时,树中没有节点,称为空树。当 n>0 时,有且仅有一个节点被称为根节点(Root),如果 n=1 ,树只有根节点一个节点。如果 n>1 ,除根节点外,将其余的节点分成m(m>0)个互不相交的数据集合,这 m 个集合每一个都要满足树的结构(有且仅有一个根节点),并且这 m 棵树都“挂”在根节点上,如此递归下去,直到所有节点都“挂”到这棵树上。其中,这 m 个集合构成的 m 棵树都被称为根节点的子树。
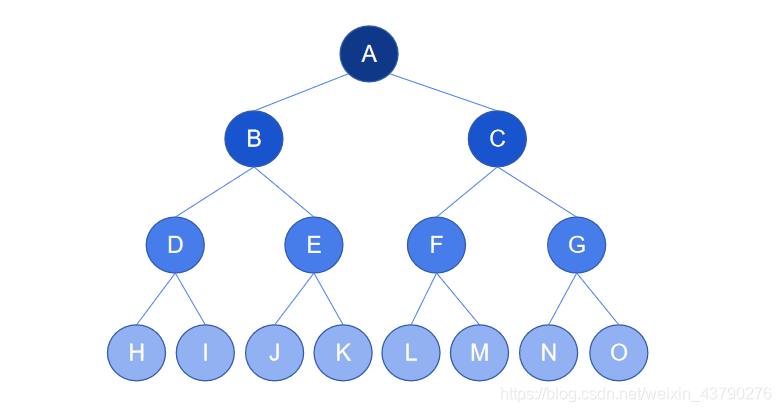
在理解树的结构和定义时,需要运用到递归的思想。以下图为例,树的节点集合为 {A,B,C,D,E,F,G,H} ,n=8,根节点为 A ,除根节点 A 外,其余节点组成了两个(m=2)集合(m1和m2),m1集合为 {B,D,E} ,m2集合为 {C,F,G,H} 。在m1中,B 为m1的根节点,除 B 以外,其余节点组成两个集合,集合 {D} 和集合 {E} ,{D} 和 {E} 都只有一个节点,分别构成一棵只有一个节点的树,它们“挂”在m1的根节点 B 上,是 B 的子树,m1构成一棵树,“挂”在根节点 A 上,m1是 A 的子树。同理,在m2中,C 为m2根节点,其余节点组成三个集合 {F} 、{G} 和 {H} ......

二、树的术语
要理解树这种数据结构,必须先理解一些常用的术语。
树由一个一个的节点组成,节点是构成复杂数据结构的基本组成单位。
1. 子节点:又称为孩子节点,一个节点所包含的子树的根节点被称为该节点的子节点。如下图中,节点 B 有两棵子树,这两棵子树的根节点为 D 和 E ,所以 D 和 E 都是 B 的子节点。
2. 父节点:又称为父亲节点,如果一个节点有子节点,则这个节点被称为其子节点的父节点。如下图中,节点 B 有两个子节点 D 和 E ,则 B 是 D 的父节点,也是 E 的父节点。
3. 兄弟节点:具有相同父节点的节点互称为兄弟节点。下图中的 D 和 E 就互为兄弟节点。
4. 堂兄弟节点:如果树的两个节点深度相同,但父节点不同,则它们互为堂兄弟节点。下图中的 D与F,D与G,D与H,D与I 都是堂兄弟节点关系。

5. 节点的祖先:从根节点开始,依次找到某节点所经路径上的所有节点都称为该节点的祖先。如下图中,节点 J 的祖先节点为 A,B,D 。
6. 节点的子孙:以某节点为根的子树中,任一节点都称为该节点的子孙。如下图中,节点 C 的子孙有 F,G,H,I,M,N,O 。

7. 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。如下图中,根节点 A 在第1层,节点 M 在第4层。
8. 节点的深度:一个节点所处的层次称为该节点的深度。如下图中,根节点 A 的深度为1,节点 M 的深度为4 。(上面解释堂兄弟节点时有用到节点的深度,现在可以回去看看)
9. 树的深度:又称为树的高度,一棵树中,最大的节点深度称为树的深度。如下图中的树深度为4。
关于深度和高度,有两种定义方式,一种是将根节点的深度定义为0,另一种是将根节点的深度定义为1。但不管怎样,每个深度为 k 的节点的子节点的深度都为 k+1 ,这是不变的。

10. 节点的度:一个节点含有的子树(或子节点)的个数称为该节点的度。如下图中, 根节点 A 的度为2,节点 C 的度为4,节点 I 的度为1,节点 O 的度为 0 。
11. 树的度:一棵树中,最大的节点度称为树的度。如下图中,最大的节点度是4,则树的度为4。
12. 叶节点:又称为终端节点,度为零的节点被称为叶节点。如下图中,节点 F,H,J,K,L,M,N,O 都是叶节点。

13. 森林:由m(m>=0)棵互不相交的树构成的集合称为森林。森林是从树延伸出来的术语,森林里的树一定是互不相交的。

三、树的特点
通过对树的定义和树的术语进行介绍,基本可以理解树这种数据结构了,总结起来,树有以下特点。
1. 如果树的节点数 n>0,根节点是唯一的,不可能存在多个根节点。
2. 没有父节点的节点称为根节点。根节点是没有父节点的。
3. 每一个非根节点有且只有一个父节点。除了根节点外,其他所有节点都有父节点,并且同一个节点只有一个父节点,不可能有多个。
4. 每个节点有零个或多个子节点。
5. 除了根节点外,子节点可以分为多个不相交的子树。这些子树一定是互不相交的。
6. 每个深度为 k 的节点的子节点的深度都为 k+1 。
四、树的分类
所有树都满足以上的特点,除此之外,一些树还具有专有的特点。根据专有的特点,可以对树进行分类。
1. 无序树:也称为自由树,树中存在一个节点,节点的子节点之间没有顺序关系。如下图中,右边的树是无序树,从树中取一个节点 D ,D 的子节点是节点 J 和节点 E,它们是没有顺序关系的,所以这是一棵无序树。
2. 有序树:树中任意节点的子节点之间有顺序关系。如下图中,左边的树是有序树,从树中任意取一个节点 C,C 的子节点是 F,G,H ,它们是有顺序关系的(字母顺序),所以这是一棵有序树。
图中的有序和无序以字母顺序作为案例,实际应用中的“有序”并不限于字母顺序、数字顺序等,实际的有序主要是指“不能互换”。

无序树的节点之间没有顺序关系,节点之间的关系不能通过代码来模拟和控制,所以基本没有实际的应用场景。
使用树这种数据结构,基本都是使用有序树,对于有序树,又可以分为以下几种。
1. 二叉树:每个节点最多含有两个子树的树称为二叉树,如下图。二叉树是最常用的树结构,可以对二叉树进一步细分(另外的文章再仔细研究)。
2. 霍夫曼树:又称为最优二叉树,是一种带权路径最短的二叉树。
3. B树:是一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多余两个子树。
可以看到,后面的两种树都是在二叉树的基础上,根据特殊的场景独立出来的,光看定义很难理解,所以以后的文章再研究。
到此这篇关于数据结构之树的概念详解的文章就介绍到这了,更多相关数据结构之树的概念内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

